Federated Learning as Variational Inference: A Scalable Expectation Propagation Approach

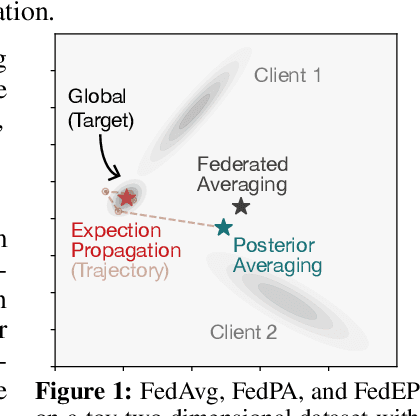
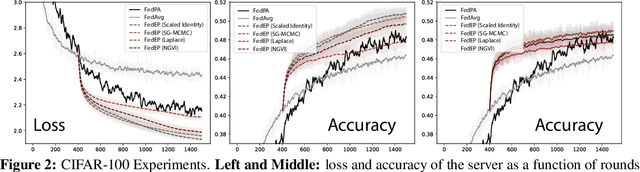
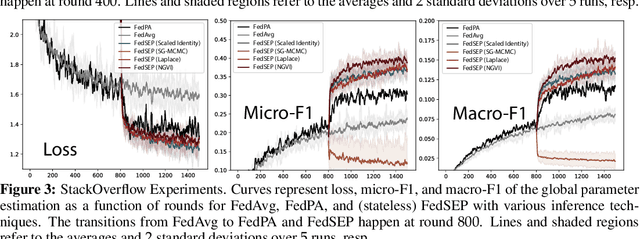
The canonical formulation of federated learning treats it as a distributed optimization problem where the model parameters are optimized against a global loss function that decomposes across client loss functions. A recent alternative formulation instead treats federated learning as a distributed inference problem, where the goal is to infer a global posterior from partitioned client data (Al-Shedivat et al., 2021). This paper extends the inference view and describes a variational inference formulation of federated learning where the goal is to find a global variational posterior that well-approximates the true posterior. This naturally motivates an expectation propagation approach to federated learning (FedEP), where approximations to the global posterior are iteratively refined through probabilistic message-passing between the central server and the clients. We conduct an extensive empirical study across various algorithmic considerations and describe practical strategies for scaling up expectation propagation to the modern federated setting. We apply FedEP on standard federated learning benchmarks and find that it outperforms strong baselines in terms of both convergence speed and accuracy.

The worst of both worlds: A comparative analysis of errors in learning from data in psychology and machine learning

Recent concerns that machine learning (ML) may be facing a reproducibility and replication crisis suggest that some published claims in ML research cannot be taken at face value. These concerns inspire analogies to the replication crisis affecting the social and medical sciences, as well as calls for greater integration of statistical approaches to causal inference and predictive modeling. A deeper understanding of what reproducibility concerns in research in supervised ML have in common with the replication crisis in experimental science can put the new concerns in perspective, and help researchers avoid "the worst of both worlds" that can emerge when ML researchers begin borrowing methodologies from explanatory modeling without understanding their limitations, and vice versa. We contribute a comparative analysis of concerns about inductive learning that arise in different stages of the modeling pipeline in causal attribution as exemplified in psychology versus predictive modeling as exemplified by ML. We identify themes that re-occur in reform discussions like overreliance on asymptotic theory and non-credible beliefs about real-world data generating processes. We argue that in both fields, claims from learning are implied to generalize outside the specific environment studied (e.g., the input dataset or subject sample, modeling implementation, etc.) but are often impossible to refute due to forms of underspecification. In particular, many errors being acknowledged in ML expose cracks in long-held beliefs that optimizing predictive accuracy using huge datasets absolves one from having to make assumptions about the underlying data generating process. We conclude by discussing rhetorical risks like error misdiagnosis that arise in times of methodological uncertainty.

Toward a Taxonomy of Trust for Probabilistic Machine Learning

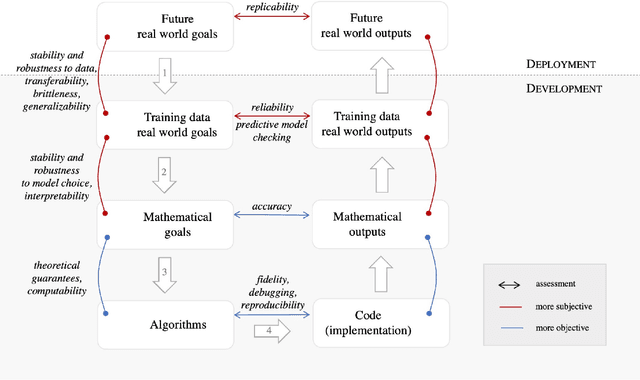
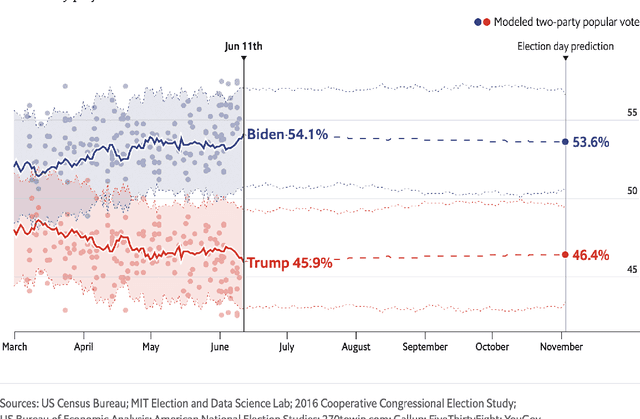
Probabilistic machine learning increasingly informs critical decisions in medicine, economics, politics, and beyond. We need evidence to support that the resulting decisions are well-founded. To aid development of trust in these decisions, we develop a taxonomy delineating where trust in an analysis can break down: (1) in the translation of real-world goals to goals on a particular set of available training data, (2) in the translation of abstract goals on the training data to a concrete mathematical problem, (3) in the use of an algorithm to solve the stated mathematical problem, and (4) in the use of a particular code implementation of the chosen algorithm. We detail how trust can fail at each step and illustrate our taxonomy with two case studies: an analysis of the efficacy of microcredit and The Economist's predictions of the 2020 US presidential election. Finally, we describe a wide variety of methods that can be used to increase trust at each step of our taxonomy. The use of our taxonomy highlights steps where existing research work on trust tends to concentrate and also steps where establishing trust is particularly challenging.

Pathfinder: Parallel quasi-Newton variational inference

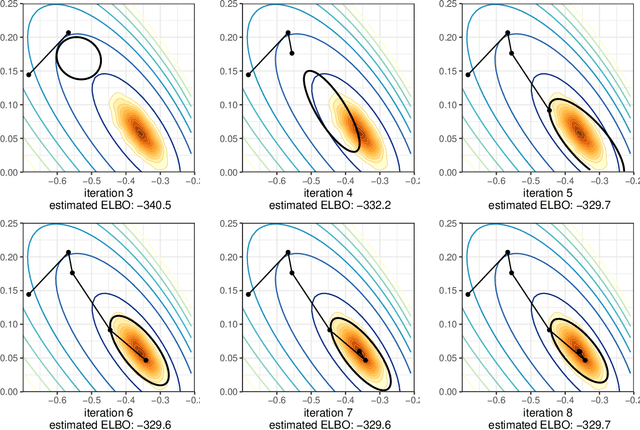
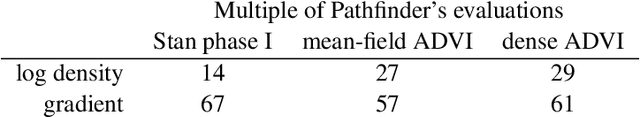
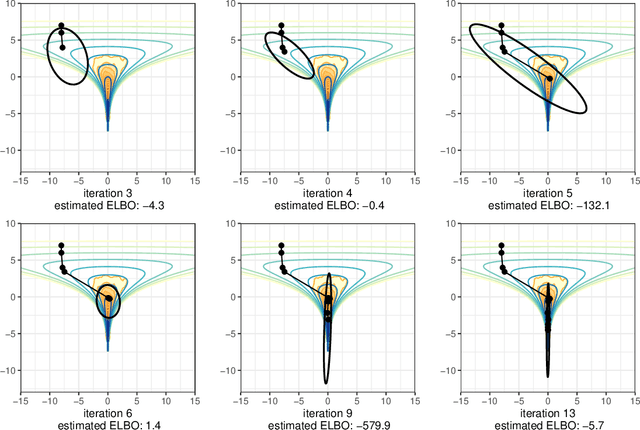
We introduce Pathfinder, a variational method for approximately sampling from differentiable log densities. Starting from a random initialization, Pathfinder locates normal approximations to the target density along a quasi-Newton optimization path, with local covariance estimated using the inverse Hessian estimates produced by the optimizer. Pathfinder returns draws from the approximation with the lowest estimated Kullback-Leibler (KL) divergence to the true posterior. We evaluate Pathfinder on a wide range of posterior distributions, demonstrating that its approximate draws are better than those from automatic differentiation variational inference (ADVI) and comparable to those produced by short chains of dynamic Hamiltonian Monte Carlo (HMC), as measured by 1-Wasserstein distance. Compared to ADVI and short dynamic HMC runs, Pathfinder requires one to two orders of magnitude fewer log density and gradient evaluations, with greater reductions for more challenging posteriors. Importance resampling over multiple runs of Pathfinder improves the diversity of approximate draws, reducing 1-Wasserstein distance further and providing a measure of robustness to optimization failures on plateaus, saddle points, or in minor modes. The Monte Carlo KL-divergence estimates are embarrassingly parallelizable in the core Pathfinder algorithm, as are multiple runs in the resampling version, further increasing Pathfinder's speed advantage with multiple cores.

Bayesian hierarchical stacking

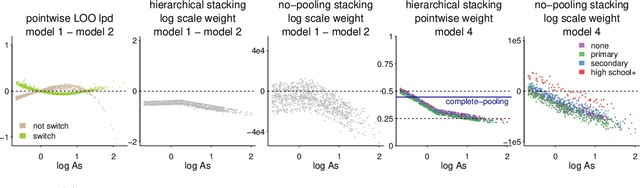
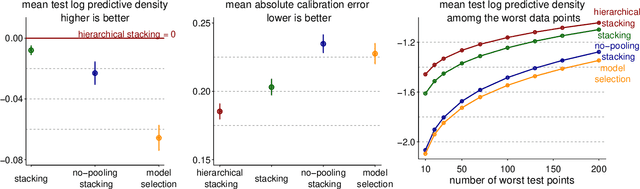
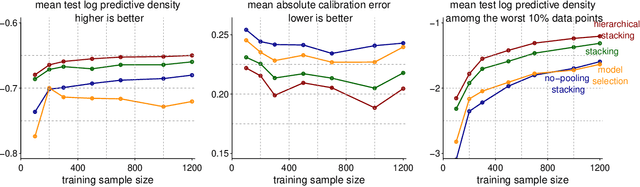
Stacking is a widely used model averaging technique that yields asymptotically optimal prediction among all linear averages. We show that stacking is most effective when the model predictive performance is heterogeneous in inputs, so that we can further improve the stacked mixture with a hierarchical model. With the input-varying yet partially-pooled model weights, hierarchical stacking improves average and conditional predictions. Our Bayesian formulation includes constant-weight (complete-pooling) stacking as a special case. We generalize to incorporate discrete and continuous inputs, other structured priors, and time-series and longitudinal data. We demonstrate on several applied problems.

Stacking for Non-mixing Bayesian Computations: The Curse and Blessing of Multimodal Posteriors

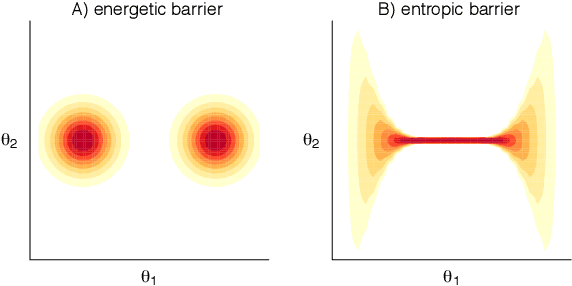
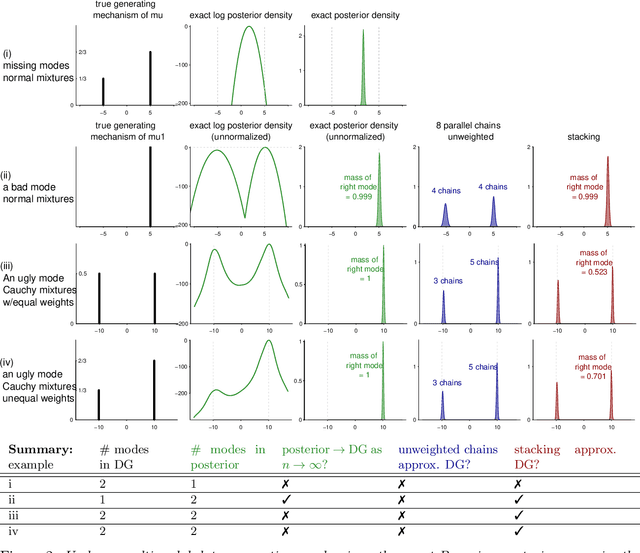
When working with multimodal Bayesian posterior distributions, Markov chain Monte Carlo (MCMC) algorithms can have difficulty moving between modes, and default variational or mode-based approximate inferences will understate posterior uncertainty. And, even if the most important modes can be found, it is difficult to evaluate their relative weights in the posterior. Here we propose an alternative approach, using parallel runs of MCMC, variational, or mode-based inference to hit as many modes or separated regions as possible, and then combining these using importance sampling based Bayesian stacking, a scalable method for constructing a weighted average of distributions so as to maximize cross-validated prediction utility. The result from stacking is not necessarily equivalent, even asymptotically, to fully Bayesian inference, but it serves many of the same goals. Under misspecified models, stacking can give better predictive performance than full Bayesian inference, hence the multimodality can be considered a blessing rather than a curse. We explore with an example where the stacked inference approximates the true data generating process from the misspecified model, an example of inconsistent inference, and non-mixing samplers. We elaborate the practical implantation in the context of latent Dirichlet allocation, Gaussian process regression, hierarchical model, variational inference in horseshoe regression, and neural networks.

Yes, but Did It Work?: Evaluating Variational Inference

While it's always possible to compute a variational approximation to a posterior distribution, it can be difficult to discover problems with this approximation. We propose two diagnostic algorithms to alleviate this problem. The Pareto-smoothed importance sampling (PSIS) diagnostic gives a goodness of fit measurement for joint distributions, while simultaneously improving the error in the estimate. The variational simulation-based calibration (VSBC) assesses the average performance of point estimates.

Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data

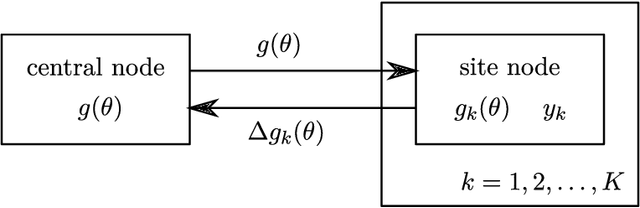
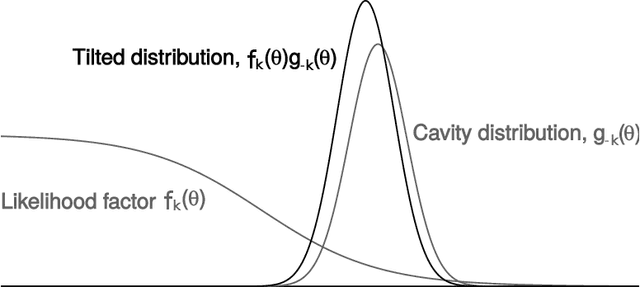
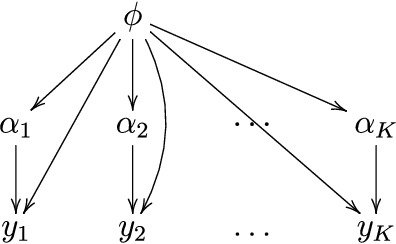
A common approach for Bayesian computation with big data is to partition the data into smaller pieces, perform local inference for each piece separately, and finally combine the results to obtain an approximation to the global posterior. Looking at this from the bottom up, one can perform separate analyses on individual sources of data and then combine these in a larger Bayesian model. In either case, the idea of distributed modeling and inference has both conceptual and computational appeal, but from the Bayesian perspective there is no general way of handling the prior distribution: if the prior is included in each separate inference, it will be multiply-counted when the inferences are combined; but if the prior is itself divided into pieces, it may not provide enough regularization for each separate computation, thus eliminating one of the key advantages of Bayesian methods. To resolve this dilemma, we propose expectation propagation (EP) as a general prototype for distributed Bayesian inference. The central idea is to factor the likelihood according to the data partitions, and to iteratively combine each factor with an approximate model of the prior and all other parts of the data, thus producing an overall approximation to the global posterior at convergence. In this paper, we give an introduction to EP and an overview of some recent developments of the method, with particular emphasis on its use in combining inferences from partitioned data. In addition to distributed modeling of large datasets, our unified treatment also includes hierarchical modeling of data with a naturally partitioned structure. The paper describes a general algorithmic framework, rather than a specific algorithm, and presents an example implementation for it.

Automatic Differentiation Variational Inference

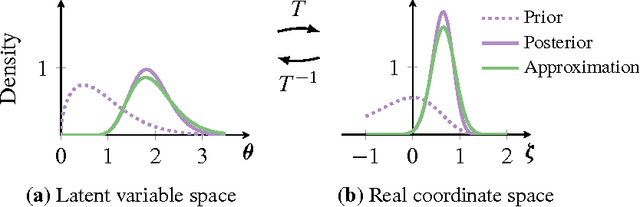
Probabilistic modeling is iterative. A scientist posits a simple model, fits it to her data, refines it according to her analysis, and repeats. However, fitting complex models to large data is a bottleneck in this process. Deriving algorithms for new models can be both mathematically and computationally challenging, which makes it difficult to efficiently cycle through the steps. To this end, we develop automatic differentiation variational inference (ADVI). Using our method, the scientist only provides a probabilistic model and a dataset, nothing else. ADVI automatically derives an efficient variational inference algorithm, freeing the scientist to refine and explore many models. ADVI supports a broad class of models-no conjugacy assumptions are required. We study ADVI across ten different models and apply it to a dataset with millions of observations. ADVI is integrated into Stan, a probabilistic programming system; it is available for immediate use.

Automatic Variational Inference in Stan

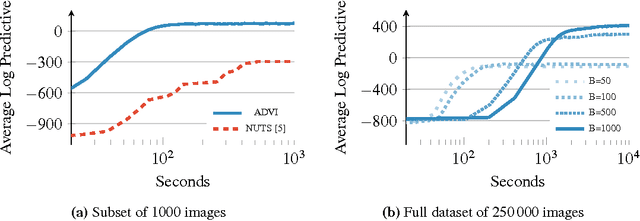
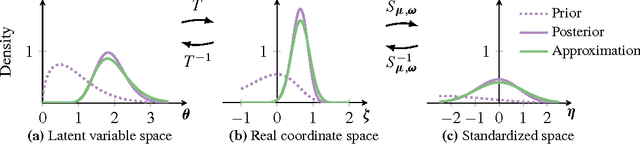
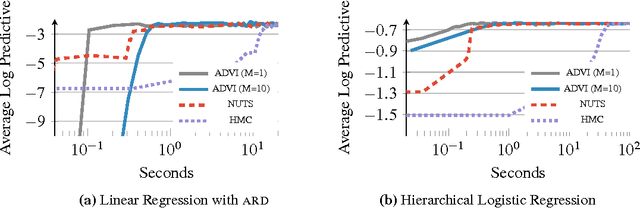
Variational inference is a scalable technique for approximate Bayesian inference. Deriving variational inference algorithms requires tedious model-specific calculations; this makes it difficult to automate. We propose an automatic variational inference algorithm, automatic differentiation variational inference (ADVI). The user only provides a Bayesian model and a dataset; nothing else. We make no conjugacy assumptions and support a broad class of models. The algorithm automatically determines an appropriate variational family and optimizes the variational objective. We implement ADVI in Stan (code available now), a probabilistic programming framework. We compare ADVI to MCMC sampling across hierarchical generalized linear models, nonconjugate matrix factorization, and a mixture model. We train the mixture model on a quarter million images. With ADVI we can use variational inference on any model we write in Stan.