Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data
Paper and Code
Mar 10, 2018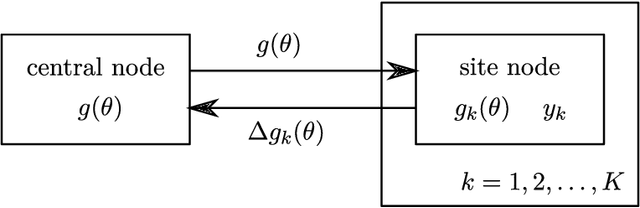
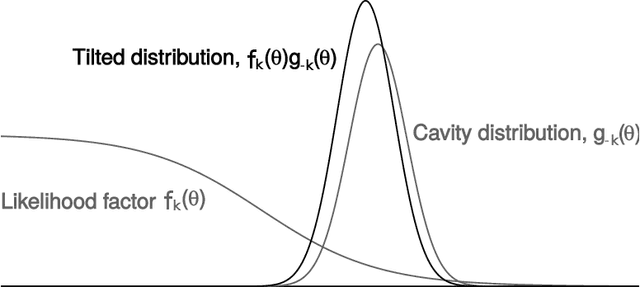
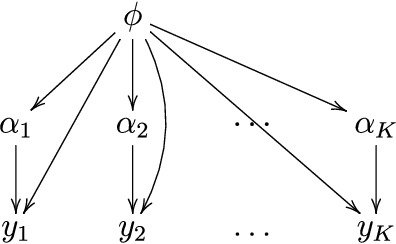
A common approach for Bayesian computation with big data is to partition the data into smaller pieces, perform local inference for each piece separately, and finally combine the results to obtain an approximation to the global posterior. Looking at this from the bottom up, one can perform separate analyses on individual sources of data and then combine these in a larger Bayesian model. In either case, the idea of distributed modeling and inference has both conceptual and computational appeal, but from the Bayesian perspective there is no general way of handling the prior distribution: if the prior is included in each separate inference, it will be multiply-counted when the inferences are combined; but if the prior is itself divided into pieces, it may not provide enough regularization for each separate computation, thus eliminating one of the key advantages of Bayesian methods. To resolve this dilemma, we propose expectation propagation (EP) as a general prototype for distributed Bayesian inference. The central idea is to factor the likelihood according to the data partitions, and to iteratively combine each factor with an approximate model of the prior and all other parts of the data, thus producing an overall approximation to the global posterior at convergence. In this paper, we give an introduction to EP and an overview of some recent developments of the method, with particular emphasis on its use in combining inferences from partitioned data. In addition to distributed modeling of large datasets, our unified treatment also includes hierarchical modeling of data with a naturally partitioned structure. The paper describes a general algorithmic framework, rather than a specific algorithm, and presents an example implementation for it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge