Pasi Jylänki
Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data
Mar 10, 2018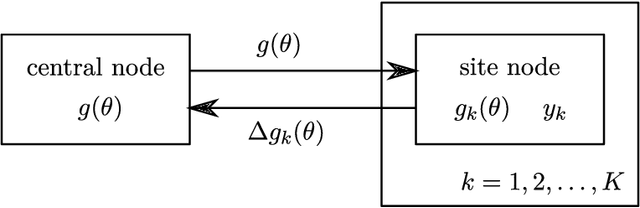
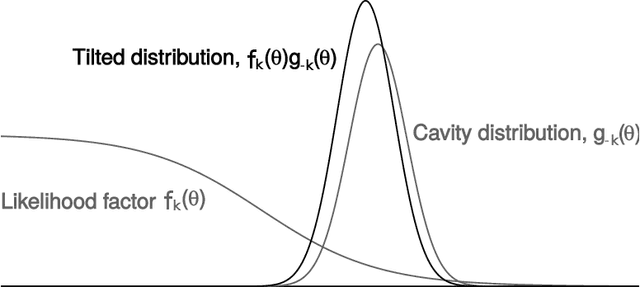
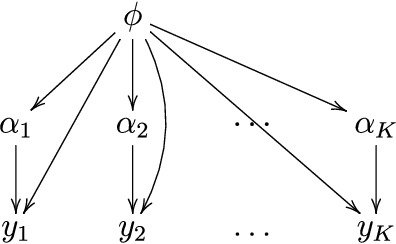
Abstract:A common approach for Bayesian computation with big data is to partition the data into smaller pieces, perform local inference for each piece separately, and finally combine the results to obtain an approximation to the global posterior. Looking at this from the bottom up, one can perform separate analyses on individual sources of data and then combine these in a larger Bayesian model. In either case, the idea of distributed modeling and inference has both conceptual and computational appeal, but from the Bayesian perspective there is no general way of handling the prior distribution: if the prior is included in each separate inference, it will be multiply-counted when the inferences are combined; but if the prior is itself divided into pieces, it may not provide enough regularization for each separate computation, thus eliminating one of the key advantages of Bayesian methods. To resolve this dilemma, we propose expectation propagation (EP) as a general prototype for distributed Bayesian inference. The central idea is to factor the likelihood according to the data partitions, and to iteratively combine each factor with an approximate model of the prior and all other parts of the data, thus producing an overall approximation to the global posterior at convergence. In this paper, we give an introduction to EP and an overview of some recent developments of the method, with particular emphasis on its use in combining inferences from partitioned data. In addition to distributed modeling of large datasets, our unified treatment also includes hierarchical modeling of data with a naturally partitioned structure. The paper describes a general algorithmic framework, rather than a specific algorithm, and presents an example implementation for it.
Regularizing Solutions to the MEG Inverse Problem Using Space-Time Separable Covariance Functions
Apr 17, 2016



Abstract:In magnetoencephalography (MEG) the conventional approach to source reconstruction is to solve the underdetermined inverse problem independently over time and space. Here we present how the conventional approach can be extended by regularizing the solution in space and time by a Gaussian process (Gaussian random field) model. Assuming a separable covariance function in space and time, the computational complexity of the proposed model becomes (without any further assumptions or restrictions) $\mathcal{O}(t^3 + n^3 + m^2n)$, where $t$ is the number of time steps, $m$ is the number of sources, and $n$ is the number of sensors. We apply the method to both simulated and empirical data, and demonstrate the efficiency and generality of our Bayesian source reconstruction approach which subsumes various classical approaches in the literature.
Bayesian Modeling with Gaussian Processes using the GPstuff Toolbox
Jul 15, 2015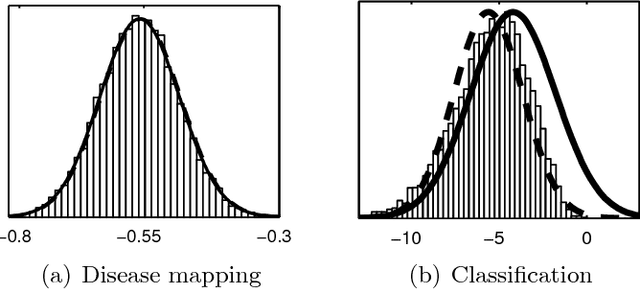
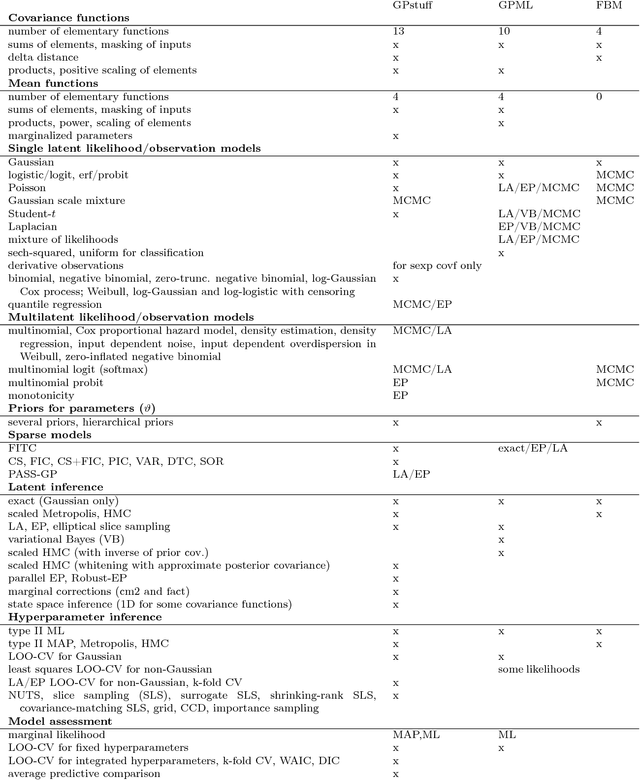
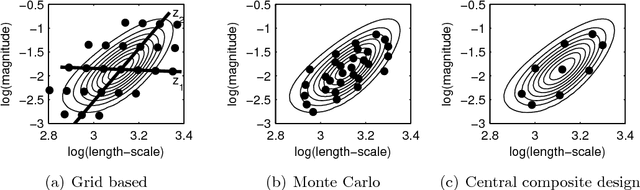
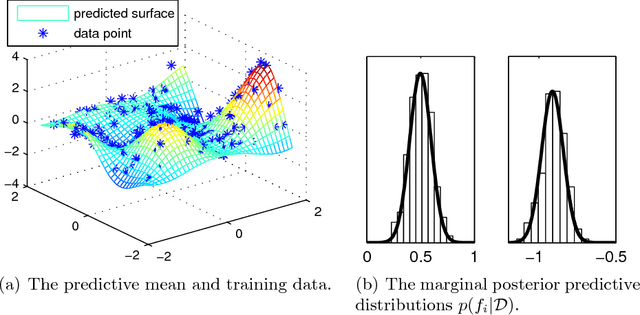
Abstract:Gaussian processes (GP) are powerful tools for probabilistic modeling purposes. They can be used to define prior distributions over latent functions in hierarchical Bayesian models. The prior over functions is defined implicitly by the mean and covariance function, which determine the smoothness and variability of the function. The inference can then be conducted directly in the function space by evaluating or approximating the posterior process. Despite their attractive theoretical properties GPs provide practical challenges in their implementation. GPstuff is a versatile collection of computational tools for GP models compatible with Linux and Windows MATLAB and Octave. It includes, among others, various inference methods, sparse approximations and tools for model assessment. In this work, we review these tools and demonstrate the use of GPstuff in several models.
Approximate Inference for Nonstationary Heteroscedastic Gaussian process Regression
Apr 22, 2014


Abstract:This paper presents a novel approach for approximate integration over the uncertainty of noise and signal variances in Gaussian process (GP) regression. Our efficient and straightforward approach can also be applied to integration over input dependent noise variance (heteroscedasticity) and input dependent signal variance (nonstationarity) by setting independent GP priors for the noise and signal variances. We use expectation propagation (EP) for inference and compare results to Markov chain Monte Carlo in two simulated data sets and three empirical examples. The results show that EP produces comparable results with less computational burden.
Expectation Propagation for Neural Networks with Sparsity-promoting Priors
Mar 27, 2013



Abstract:We propose a novel approach for nonlinear regression using a two-layer neural network (NN) model structure with sparsity-favoring hierarchical priors on the network weights. We present an expectation propagation (EP) approach for approximate integration over the posterior distribution of the weights, the hierarchical scale parameters of the priors, and the residual scale. Using a factorized posterior approximation we derive a computationally efficient algorithm, whose complexity scales similarly to an ensemble of independent sparse linear models. The approach enables flexible definition of weight priors with different sparseness properties such as independent Laplace priors with a common scale parameter or Gaussian automatic relevance determination (ARD) priors with different relevance parameters for all inputs. The approach can be extended beyond standard activation functions and NN model structures to form flexible nonlinear predictors from multiple sparse linear models. The effects of the hierarchical priors and the predictive performance of the algorithm are assessed using both simulated and real-world data. Comparisons are made to two alternative models with ARD priors: a Gaussian process with a NN covariance function and marginal maximum a posteriori estimates of the relevance parameters, and a NN with Markov chain Monte Carlo integration over all the unknown model parameters.
Nested Expectation Propagation for Gaussian Process Classification with a Multinomial Probit Likelihood
Jul 16, 2012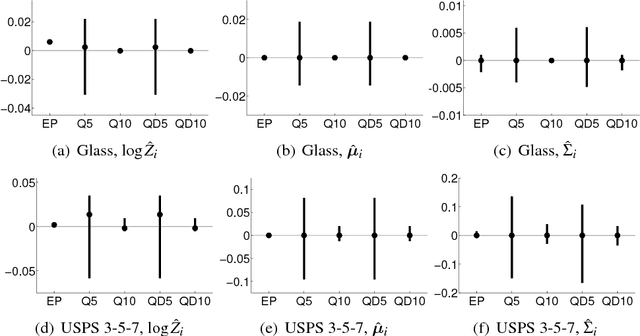
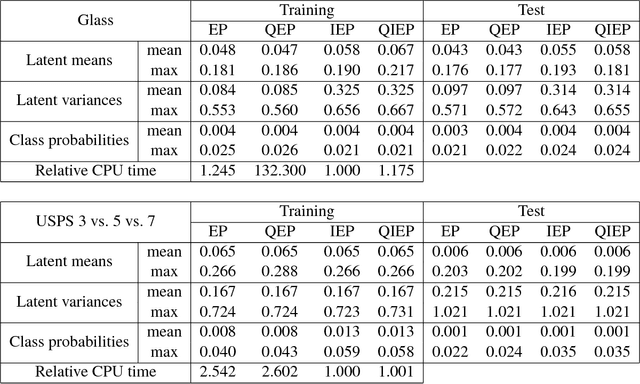
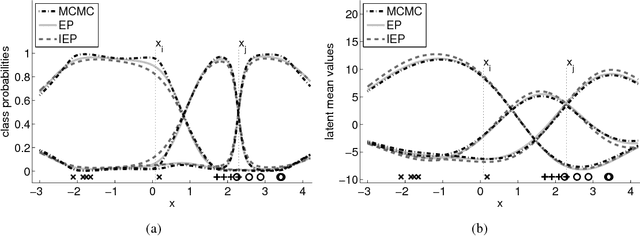

Abstract:We consider probabilistic multinomial probit classification using Gaussian process (GP) priors. The challenges with the multiclass GP classification are the integration over the non-Gaussian posterior distribution, and the increase of the number of unknown latent variables as the number of target classes grows. Expectation propagation (EP) has proven to be a very accurate method for approximate inference but the existing EP approaches for the multinomial probit GP classification rely on numerical quadratures or independence assumptions between the latent values from different classes to facilitate the computations. In this paper, we propose a novel nested EP approach which does not require numerical quadratures, and approximates accurately all between-class posterior dependencies of the latent values, but still scales linearly in the number of classes. The predictive accuracy of the nested EP approach is compared to Laplace, variational Bayes, and Markov chain Monte Carlo (MCMC) approximations with various benchmark data sets. In the experiments nested EP was the most consistent method with respect to MCMC sampling, but the differences between the compared methods were small if only the classification accuracy is concerned.
Gaussian Process Regression with a Student-t Likelihood
Jun 22, 2011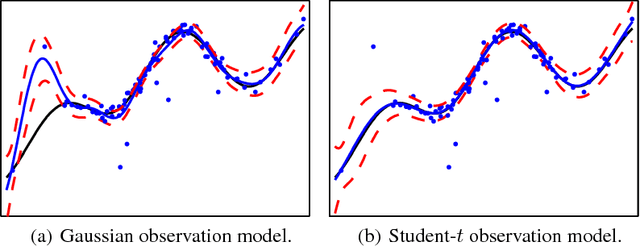

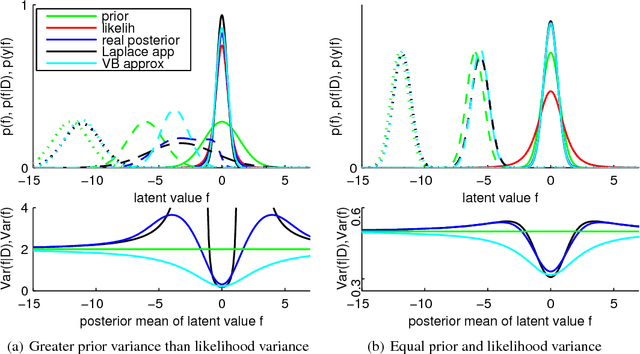
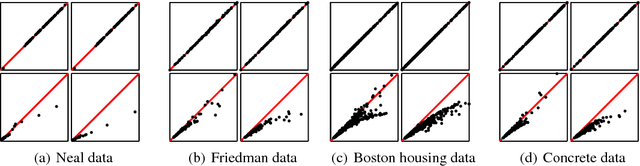
Abstract:This paper considers the robust and efficient implementation of Gaussian process regression with a Student-t observation model. The challenge with the Student-t model is the analytically intractable inference which is why several approximative methods have been proposed. The expectation propagation (EP) has been found to be a very accurate method in many empirical studies but the convergence of the EP is known to be problematic with models containing non-log-concave site functions such as the Student-t distribution. In this paper we illustrate the situations where the standard EP fails to converge and review different modifications and alternative algorithms for improving the convergence. We demonstrate that convergence problems may occur during the type-II maximum a posteriori (MAP) estimation of the hyperparameters and show that the standard EP may not converge in the MAP values in some difficult cases. We present a robust implementation which relies primarily on parallel EP updates and utilizes a moment-matching-based double-loop algorithm with adaptively selected step size in difficult cases. The predictive performance of the EP is compared to the Laplace, variational Bayes, and Markov chain Monte Carlo approximations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge