Correcting boundary over-exploration deficiencies in Bayesian optimization with virtual derivative sign observations

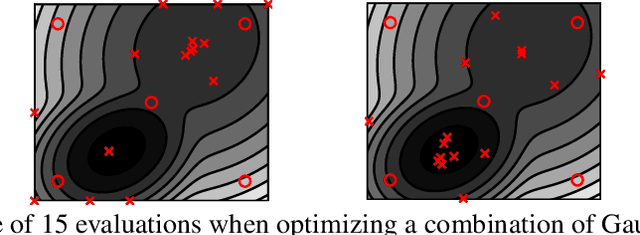
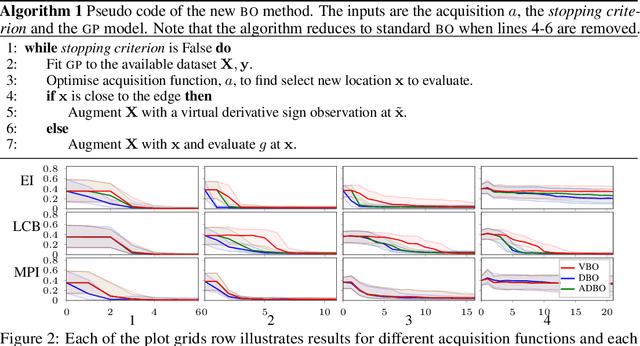
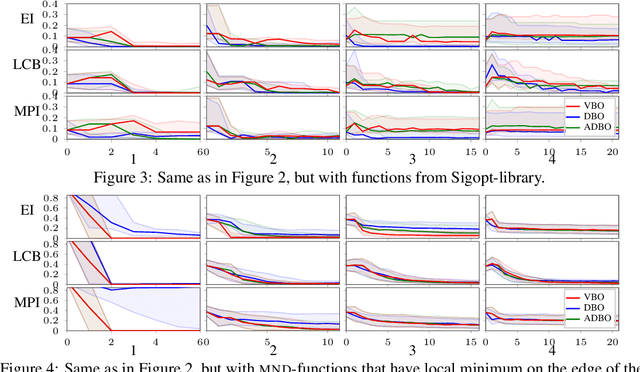
Bayesian optimization (BO) is a global optimization strategy designed to find the minimum of an expensive black-box function, typically defined on a compact subset of $\mathcal{R}^d$, by using a Gaussian process (GP) as a surrogate model for the objective. Although currently available acquisition functions address this goal with different degree of success, an over-exploration effect of the contour of the search space is typically observed. However, in problems like the configuration of machine learning algorithms, the function domain is conservatively large and with a high probability the global minimum does not sit on the boundary of the domain. We propose a method to incorporate this knowledge into the search process by adding virtual derivative observations in the \gp at the boundary of the search space. We use the properties of GPs to impose conditions on the partial derivatives of the objective. The method is applicable with any acquisition function, it is easy to use and consistently reduces the number of evaluations required to optimize the objective irrespective of the acquisition used. We illustrate the benefits of our approach in an extensive experimental comparison.

Bayesian Modeling with Gaussian Processes using the GPstuff Toolbox

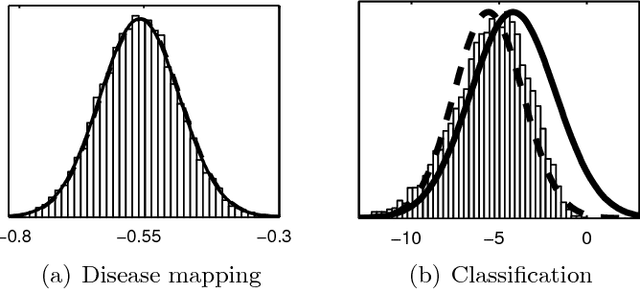
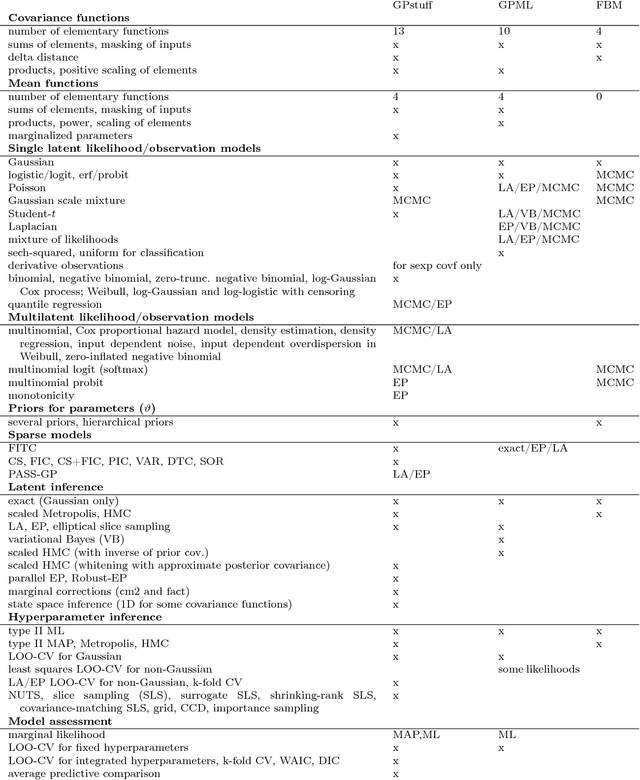
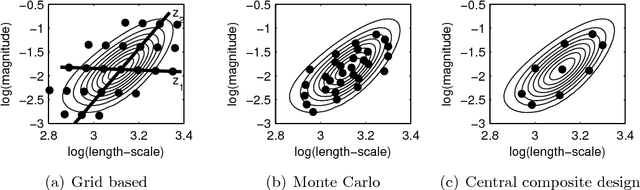
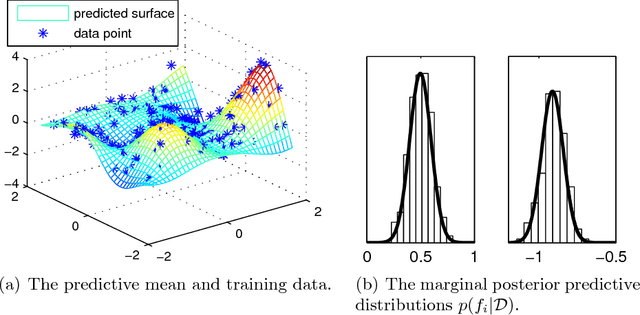
Gaussian processes (GP) are powerful tools for probabilistic modeling purposes. They can be used to define prior distributions over latent functions in hierarchical Bayesian models. The prior over functions is defined implicitly by the mean and covariance function, which determine the smoothness and variability of the function. The inference can then be conducted directly in the function space by evaluating or approximating the posterior process. Despite their attractive theoretical properties GPs provide practical challenges in their implementation. GPstuff is a versatile collection of computational tools for GP models compatible with Linux and Windows MATLAB and Octave. It includes, among others, various inference methods, sparse approximations and tools for model assessment. In this work, we review these tools and demonstrate the use of GPstuff in several models.

Modelling local and global phenomena with sparse Gaussian processes

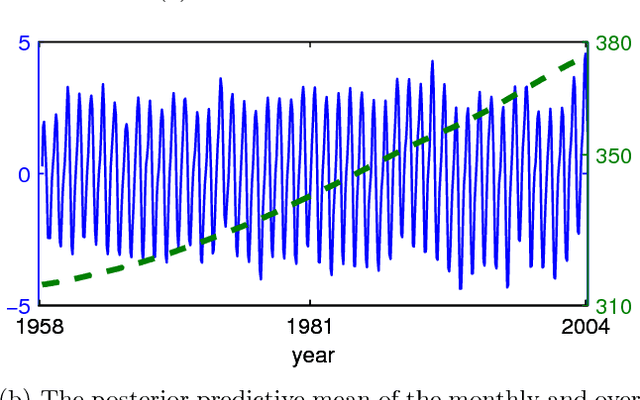
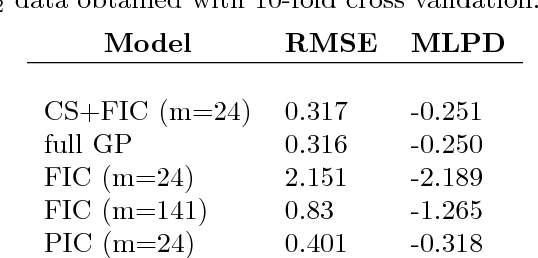
Much recent work has concerned sparse approximations to speed up the Gaussian process regression from the unfavorable O(n3) scaling in computational time to O(nm2). Thus far, work has concentrated on models with one covariance function. However, in many practical situations additive models with multiple covariance functions may perform better, since the data may contain both long and short length-scale phenomena. The long length-scales can be captured with global sparse approximations, such as fully independent conditional (FIC), and the short length-scales can be modeled naturally by covariance functions with compact support (CS). CS covariance functions lead to naturally sparse covariance matrices, which are computationally cheaper to handle than full covariance matrices. In this paper, we propose a new sparse Gaussian process model with two additive components: FIC for the long length-scales and CS covariance function for the short length-scales. We give theoretical and experimental results and show that under certain conditions the proposed model has the same computational complexity as FIC. We also compare the model performance of the proposed model to additive models approximated by fully and partially independent conditional (PIC). We use real data sets and show that our model outperforms FIC and PIC approximations for data sets with two additive phenomena.

Speeding up the binary Gaussian process classification

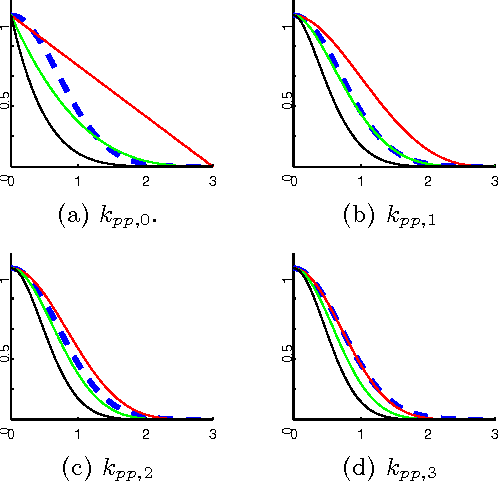
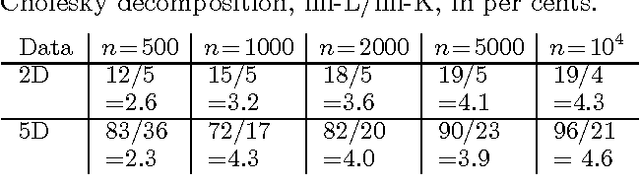
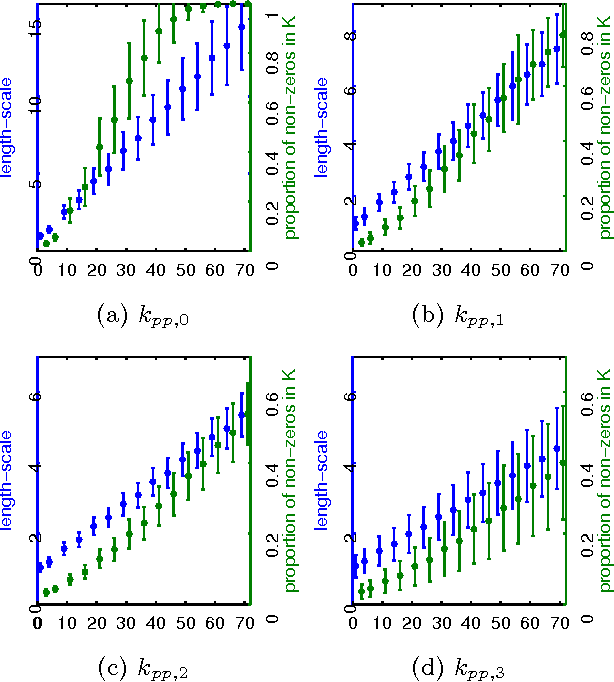
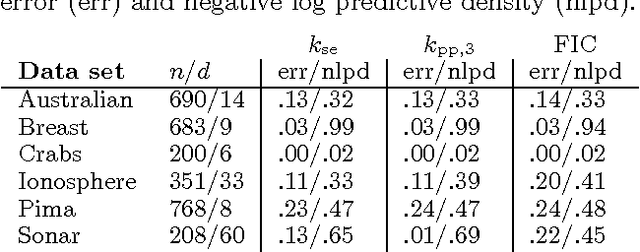
Gaussian processes (GP) are attractive building blocks for many probabilistic models. Their drawbacks, however, are the rapidly increasing inference time and memory requirement alongside increasing data. The problem can be alleviated with compactly supported (CS) covariance functions, which produce sparse covariance matrices that are fast in computations and cheap to store. CS functions have previously been used in GP regression but here the focus is in a classification problem. This brings new challenges since the posterior inference has to be done approximately. We utilize the expectation propagation algorithm and show how its standard implementation has to be modified to obtain computational benefits from the sparse covariance matrices. We study four CS covariance functions and show that they may lead to substantial speed up in the inference time compared to globally supported functions.

Gaussian Process Regression with a Student-t Likelihood

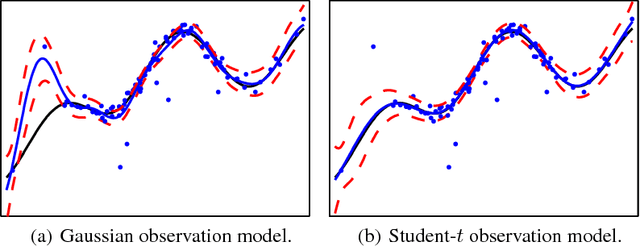
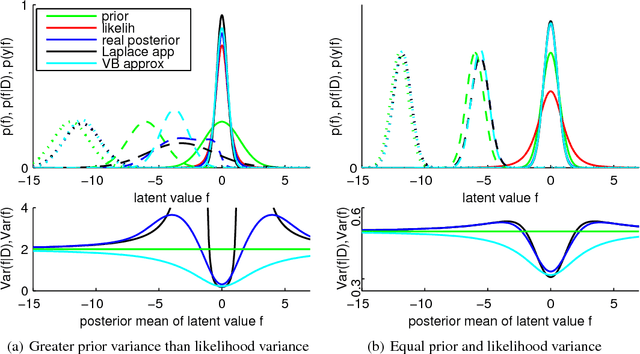
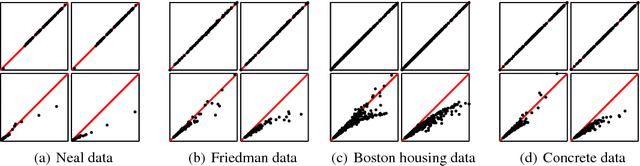
This paper considers the robust and efficient implementation of Gaussian process regression with a Student-t observation model. The challenge with the Student-t model is the analytically intractable inference which is why several approximative methods have been proposed. The expectation propagation (EP) has been found to be a very accurate method in many empirical studies but the convergence of the EP is known to be problematic with models containing non-log-concave site functions such as the Student-t distribution. In this paper we illustrate the situations where the standard EP fails to converge and review different modifications and alternative algorithms for improving the convergence. We demonstrate that convergence problems may occur during the type-II maximum a posteriori (MAP) estimation of the hyperparameters and show that the standard EP may not converge in the MAP values in some difficult cases. We present a robust implementation which relies primarily on parallel EP updates and utilizes a moment-matching-based double-loop algorithm with adaptively selected step size in difficult cases. The predictive performance of the EP is compared to the Laplace, variational Bayes, and Markov chain Monte Carlo approximations.