Correcting boundary over-exploration deficiencies in Bayesian optimization with virtual derivative sign observations
Paper and Code
Sep 21, 2018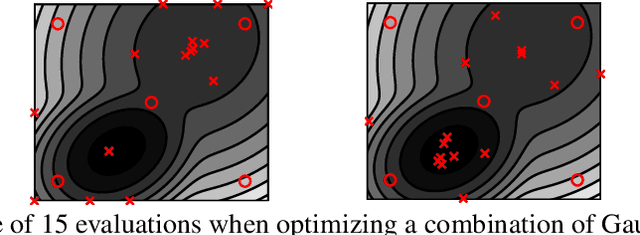
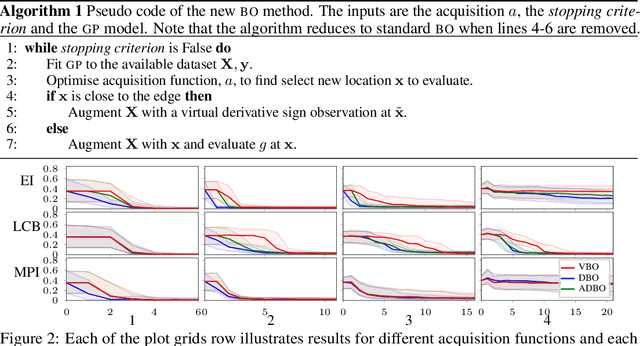
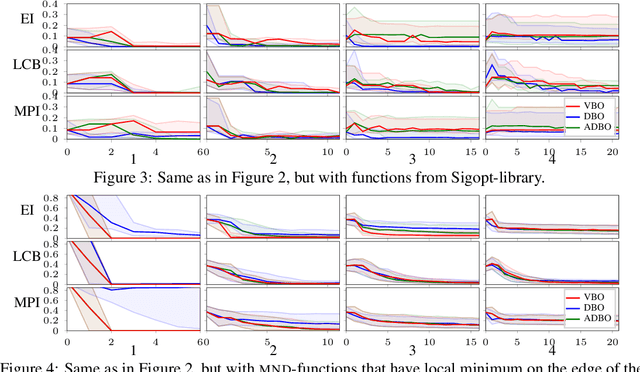
Bayesian optimization (BO) is a global optimization strategy designed to find the minimum of an expensive black-box function, typically defined on a compact subset of $\mathcal{R}^d$, by using a Gaussian process (GP) as a surrogate model for the objective. Although currently available acquisition functions address this goal with different degree of success, an over-exploration effect of the contour of the search space is typically observed. However, in problems like the configuration of machine learning algorithms, the function domain is conservatively large and with a high probability the global minimum does not sit on the boundary of the domain. We propose a method to incorporate this knowledge into the search process by adding virtual derivative observations in the \gp at the boundary of the search space. We use the properties of GPs to impose conditions on the partial derivatives of the objective. The method is applicable with any acquisition function, it is easy to use and consistently reduces the number of evaluations required to optimize the objective irrespective of the acquisition used. We illustrate the benefits of our approach in an extensive experimental comparison.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge