Good practices for Bayesian Optimization of high dimensional structured spaces

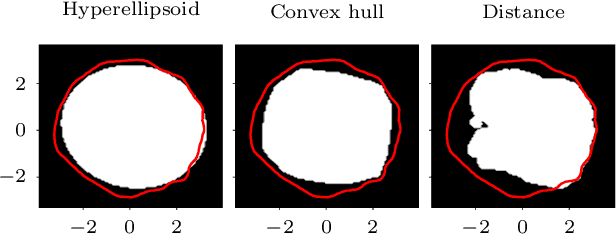
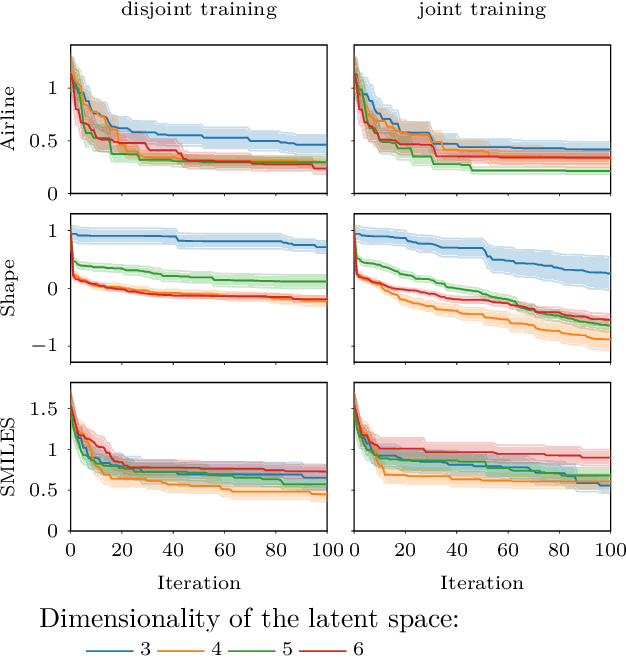
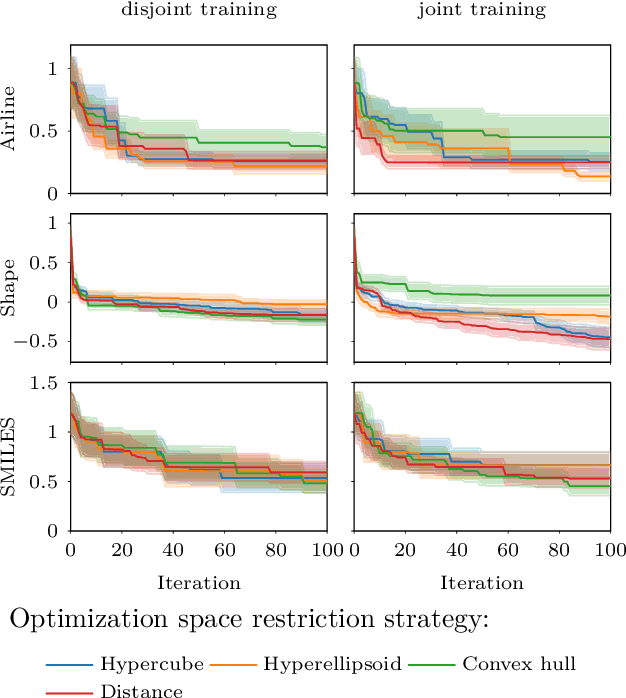
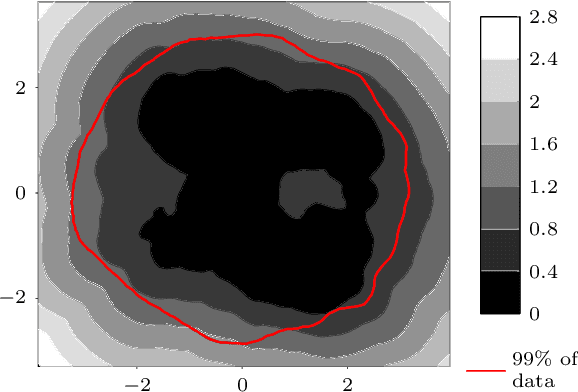
The increasing availability of structured but high dimensional data has opened new opportunities for optimization. One emerging and promising avenue is the exploration of unsupervised methods for projecting structured high dimensional data into low dimensional continuous representations, simplifying the optimization problem and enabling the application of traditional optimization methods. However, this line of research has been purely methodological with little connection to the needs of practitioners so far. In this paper, we study the effect of different search space design choices for performing Bayesian Optimization in high dimensional structured datasets. In particular, we analyse the influence of the dimensionality of the latent space, the role of the acquisition function and evaluate new methods to automatically define the optimization bounds in the latent space. Finally, based on experimental results using synthetic and real datasets, we provide recommendations for the practitioners.

Preferential Batch Bayesian Optimization

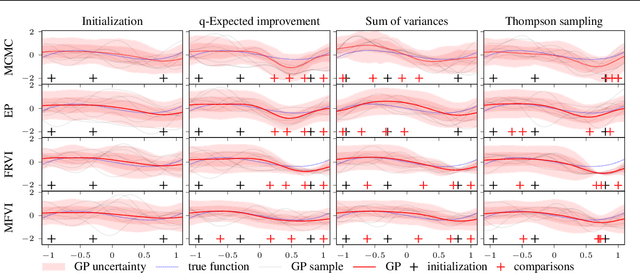
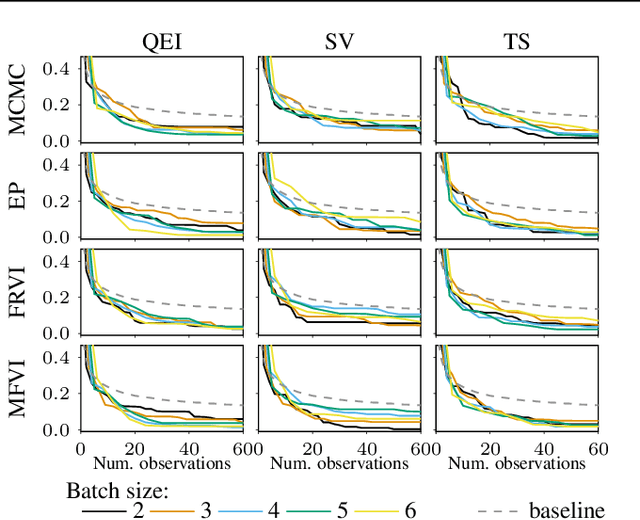
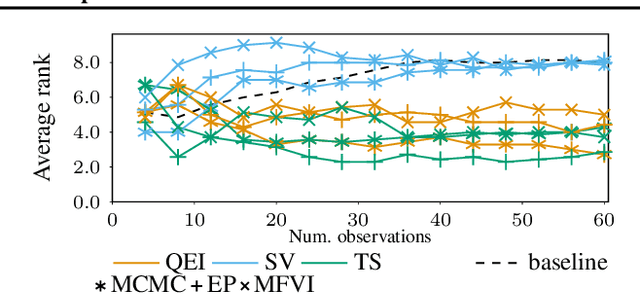
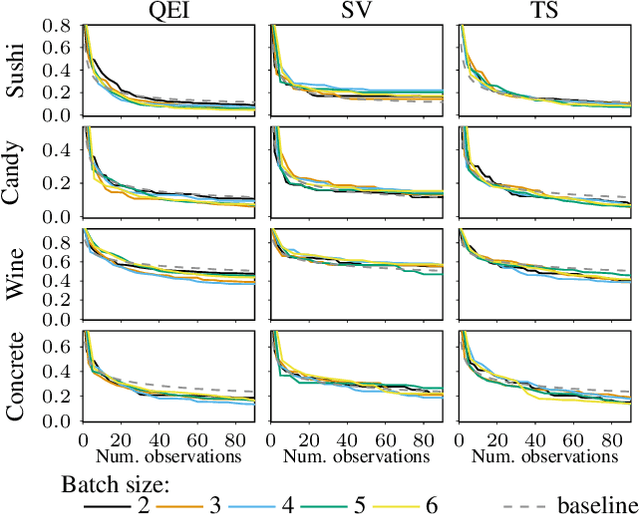
Most research in Bayesian optimization (BO) has focused on direct feedback scenarios, where one has access to exact, or perturbed, values of some expensive-to-evaluate objective. This direction has been mainly driven by the use of BO in machine learning hyper-parameter configuration problems. However, in domains such as modelling human preferences, A/B tests or recommender systems, there is a need of methods that are able to replace direct feedback with preferential feedback, obtained via rankings or pairwise comparisons. In this work, we present Preferential Batch Bayesian Optimization (PBBO), a new framework that allows to find the optimum of a latent function of interest, given any type of parallel preferential feedback for a group of two or more points. We do so by using a Gaussian process model with a likelihood specially designed to enable parallel and efficient data collection mechanisms, which are key in modern machine learning. We show how the acquisitions developed under this framework generalize and augment previous approaches in Bayesian optimization, expanding the use of these techniques to a wider range of domains. An extensive simulation study shows the benefits of this approach, both with simulated functions and four real data sets.

Active Learning for Decision-Making from Imbalanced Observational Data

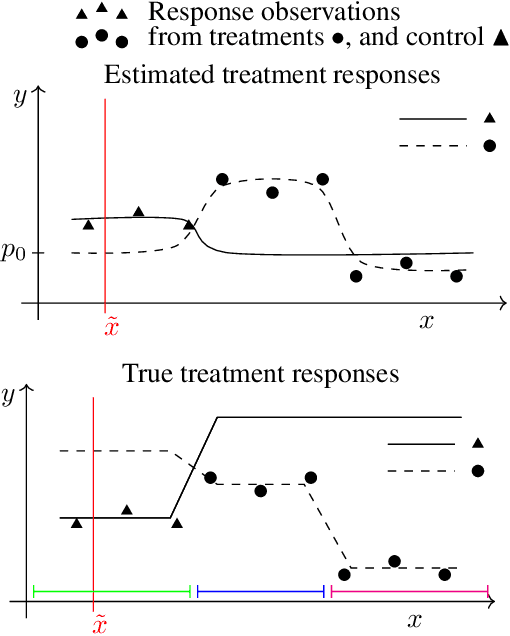
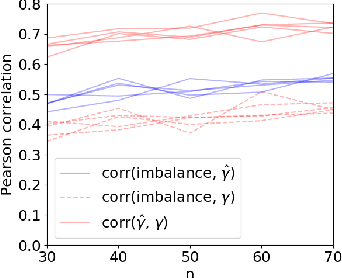
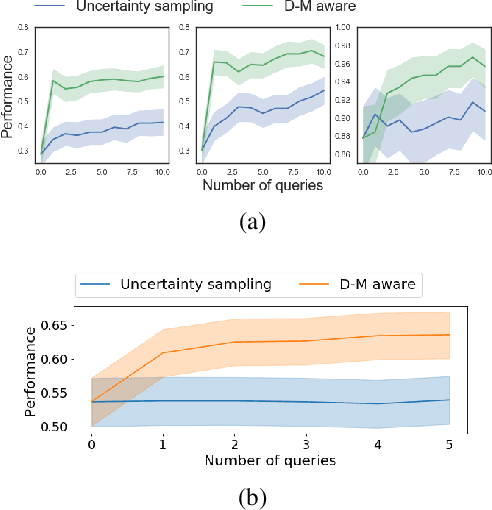
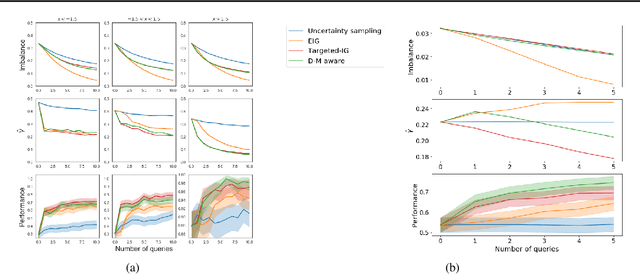
Machine learning can help personalized decision support by learning models to predict individual treatment effects (ITE). This work studies the reliability of prediction-based decision-making in a task of deciding which action $a$ to take for a target unit after observing its covariates $\tilde{x}$ and predicted outcomes $\hat{p}(\tilde{y} \mid \tilde{x}, a)$. An example case is personalized medicine and the decision of which treatment to give to a patient. A common problem when learning these models from observational data is imbalance, that is, difference in treated/control covariate distributions, which is known to increase the upper bound of the expected ITE estimation error. We propose to assess the decision-making reliability by estimating the ITE model's Type S error rate, which is the probability of the model inferring the sign of the treatment effect wrong. Furthermore, we use the estimated reliability as a criterion for active learning, in order to collect new (possibly expensive) observations, instead of making a forced choice based on unreliable predictions. We demonstrate the effectiveness of this decision-making aware active learning in two decision-making tasks: in simulated data with binary outcomes and in a medical dataset with synthetic and continuous treatment outcomes.

Correcting boundary over-exploration deficiencies in Bayesian optimization with virtual derivative sign observations

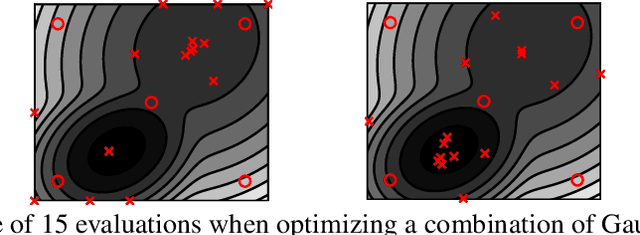
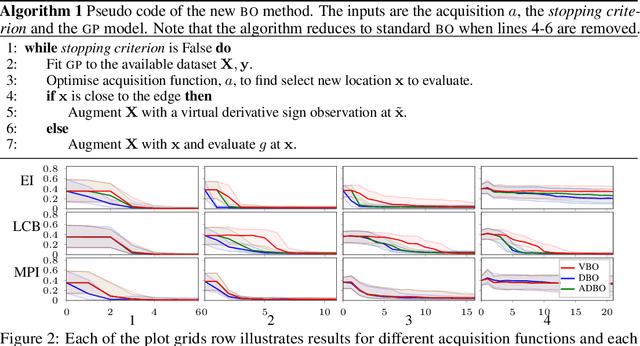
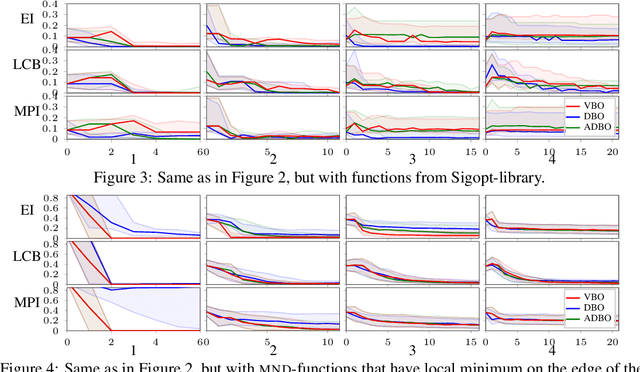
Bayesian optimization (BO) is a global optimization strategy designed to find the minimum of an expensive black-box function, typically defined on a compact subset of $\mathcal{R}^d$, by using a Gaussian process (GP) as a surrogate model for the objective. Although currently available acquisition functions address this goal with different degree of success, an over-exploration effect of the contour of the search space is typically observed. However, in problems like the configuration of machine learning algorithms, the function domain is conservatively large and with a high probability the global minimum does not sit on the boundary of the domain. We propose a method to incorporate this knowledge into the search process by adding virtual derivative observations in the \gp at the boundary of the search space. We use the properties of GPs to impose conditions on the partial derivatives of the objective. The method is applicable with any acquisition function, it is easy to use and consistently reduces the number of evaluations required to optimize the objective irrespective of the acquisition used. We illustrate the benefits of our approach in an extensive experimental comparison.