Amortized Bayesian Workflow (Extended Abstract)

Bayesian inference often faces a trade-off between computational speed and sampling accuracy. We propose an adaptive workflow that integrates rapid amortized inference with gold-standard MCMC techniques to achieve both speed and accuracy when performing inference on many observed datasets. Our approach uses principled diagnostics to guide the choice of inference method for each dataset, moving along the Pareto front from fast amortized sampling to slower but guaranteed-accurate MCMC when necessary. By reusing computations across steps, our workflow creates synergies between amortized and MCMC-based inference. We demonstrate the effectiveness of this integrated approach on a generalized extreme value task with 1000 observed data sets, showing 90x time efficiency gains while maintaining high posterior quality.

Active Learning of Molecular Data for Task-Specific Objectives

Active learning (AL) has shown promise for being a particularly data-efficient machine learning approach. Yet, its performance depends on the application and it is not clear when AL practitioners can expect computational savings. Here, we carry out a systematic AL performance assessment for three diverse molecular datasets and two common scientific tasks: compiling compact, informative datasets and targeted molecular searches. We implemented AL with Gaussian processes (GP) and used the many-body tensor as molecular representation. For the first task, we tested different data acquisition strategies, batch sizes and GP noise settings. AL was insensitive to the acquisition batch size and we observed the best AL performance for the acquisition strategy that combines uncertainty reduction with clustering to promote diversity. However, for optimal GP noise settings, AL did not outperform randomized selection of data points. Conversely, for targeted searches, AL outperformed random sampling and achieved data savings up to 64%. Our analysis provides insight into this task-specific performance difference in terms of target distributions and data collection strategies. We established that the performance of AL depends on the relative distribution of the target molecules in comparison to the total dataset distribution, with the largest computational savings achieved when their overlap is minimal.

Robust, Automated, and Accurate Black-box Variational Inference

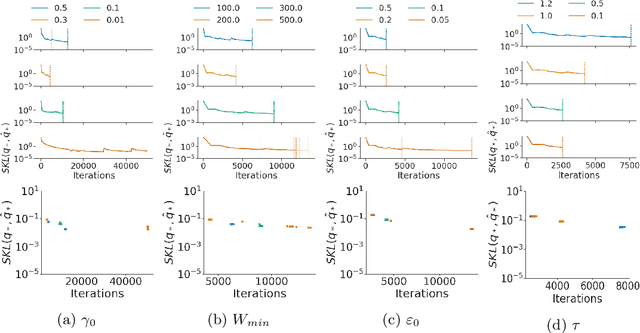
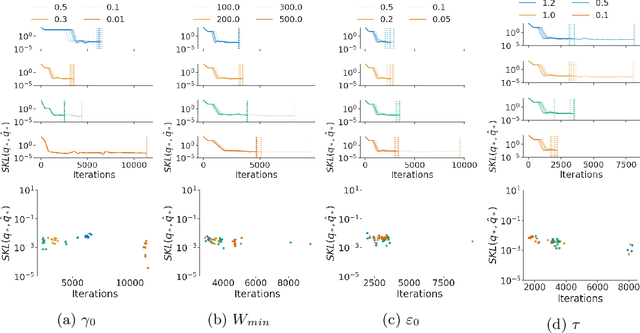
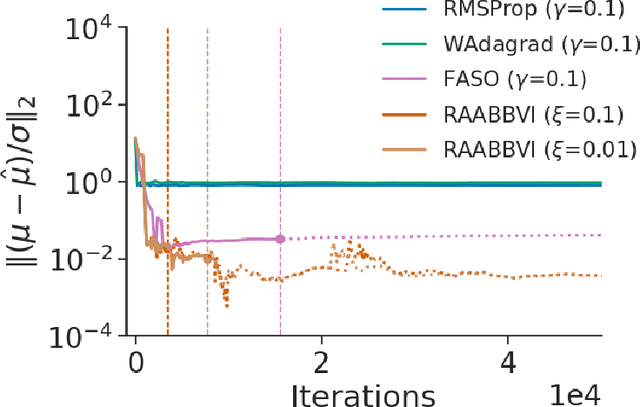
Black-box variational inference (BBVI) now sees widespread use in machine learning and statistics as a fast yet flexible alternative to Markov chain Monte Carlo methods for approximate Bayesian inference. However, stochastic optimization methods for BBVI remain unreliable and require substantial expertise and hand-tuning to apply effectively. In this paper, we propose Robust, Automated, and Accurate BBVI (RAABBVI), a framework for reliable BBVI optimization. RAABBVI is based on rigorously justified automation techniques, includes just a small number of intuitive tuning parameters, and detects inaccurate estimates of the optimal variational approximation. RAABBVI adaptively decreases the learning rate by detecting convergence of the fixed--learning-rate iterates, then estimates the symmetrized Kullback--Leiber (KL) divergence between the current variational approximation and the optimal one. It also employs a novel optimization termination criterion that enables the user to balance desired accuracy against computational cost by comparing (i) the predicted relative decrease in the symmetrized KL divergence if a smaller learning were used and (ii) the predicted computation required to converge with the smaller learning rate. We validate the robustness and accuracy of RAABBVI through carefully designed simulation studies and on a diverse set of real-world model and data examples.

Pathfinder: Parallel quasi-Newton variational inference

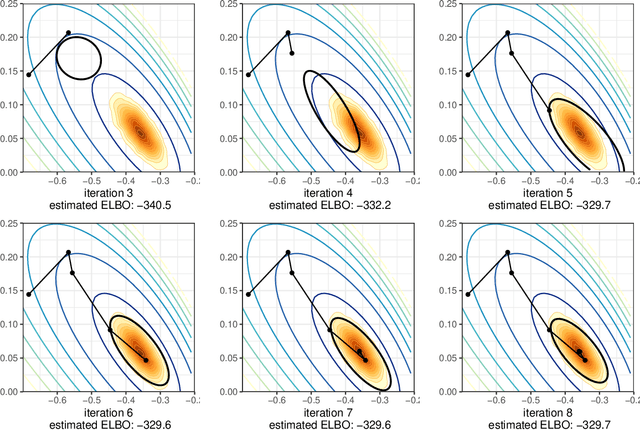
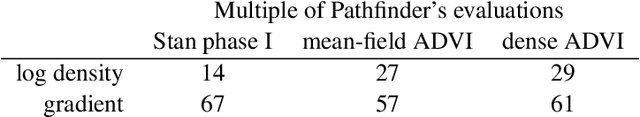
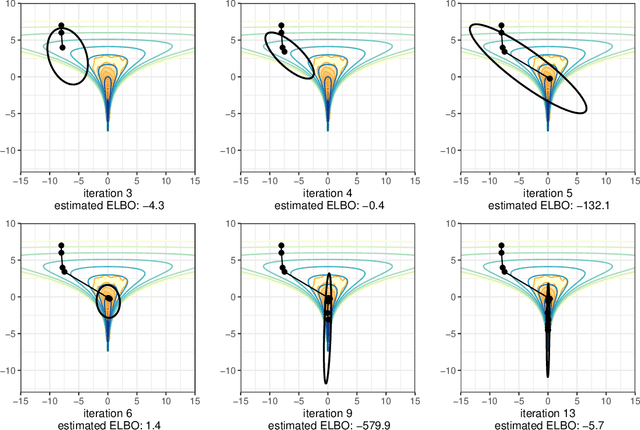
We introduce Pathfinder, a variational method for approximately sampling from differentiable log densities. Starting from a random initialization, Pathfinder locates normal approximations to the target density along a quasi-Newton optimization path, with local covariance estimated using the inverse Hessian estimates produced by the optimizer. Pathfinder returns draws from the approximation with the lowest estimated Kullback-Leibler (KL) divergence to the true posterior. We evaluate Pathfinder on a wide range of posterior distributions, demonstrating that its approximate draws are better than those from automatic differentiation variational inference (ADVI) and comparable to those produced by short chains of dynamic Hamiltonian Monte Carlo (HMC), as measured by 1-Wasserstein distance. Compared to ADVI and short dynamic HMC runs, Pathfinder requires one to two orders of magnitude fewer log density and gradient evaluations, with greater reductions for more challenging posteriors. Importance resampling over multiple runs of Pathfinder improves the diversity of approximate draws, reducing 1-Wasserstein distance further and providing a measure of robustness to optimization failures on plateaus, saddle points, or in minor modes. The Monte Carlo KL-divergence estimates are embarrassingly parallelizable in the core Pathfinder algorithm, as are multiple runs in the resampling version, further increasing Pathfinder's speed advantage with multiple cores.

Challenges and Opportunities in High-dimensional Variational Inference

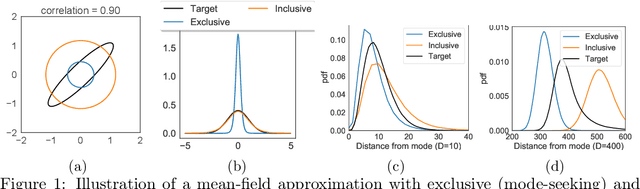
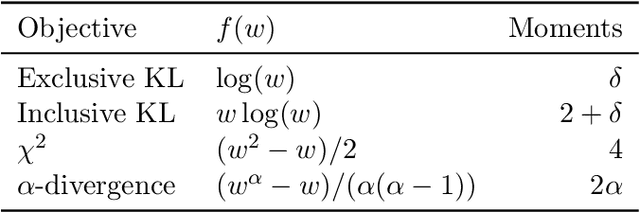
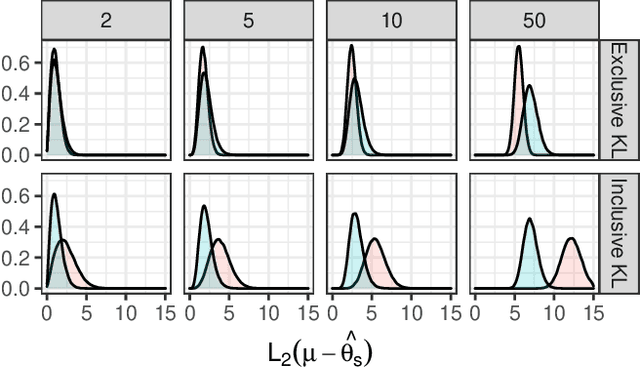
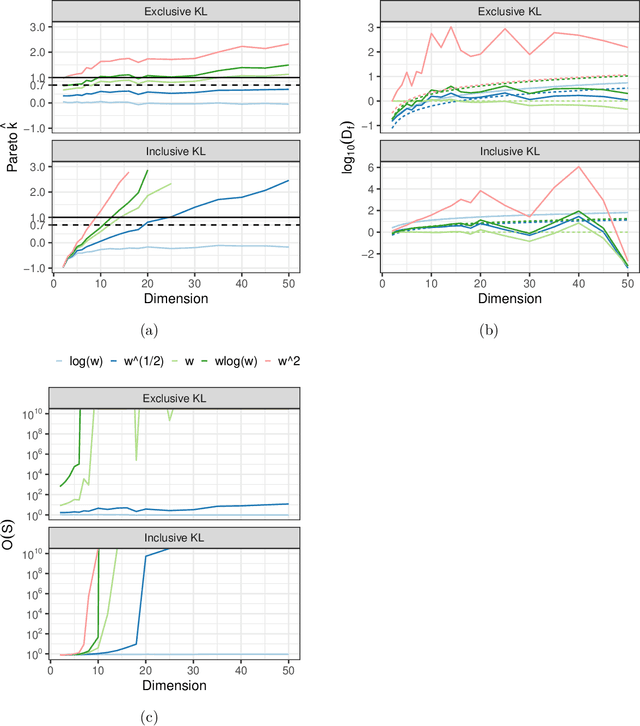
We explore the limitations of and best practices for using black-box variational inference to estimate posterior summaries of the model parameters. By taking an importance sampling perspective, we are able to explain and empirically demonstrate: 1) why the intuitions about the behavior of approximate families and divergences for low-dimensional posteriors fail for higher-dimensional posteriors, 2) how we can diagnose the pre-asymptotic reliability of variational inference in practice by examining the behavior of the density ratios (i.e., importance weights), 3) why the choice of variational objective is not as relevant for higher-dimensional posteriors, and 4) why, although flexible variational families can provide some benefits in higher dimensions, they also introduce additional optimization challenges. Based on these findings, for high-dimensional posteriors we recommend using the exclusive KL divergence that is most stable and easiest to optimize, and then focusing on improving the variational family or using model parameter transformations to make the posterior more similar to the approximating family. Our results also show that in low to moderate dimensions, heavy-tailed variational families and mass-covering divergences can increase the chances that the approximation can be improved by importance sampling.

Bayesian hierarchical stacking

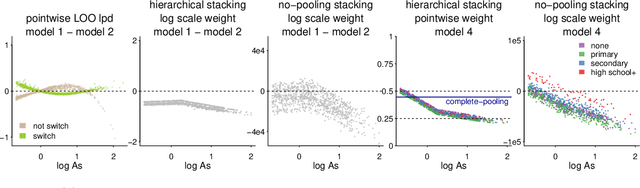
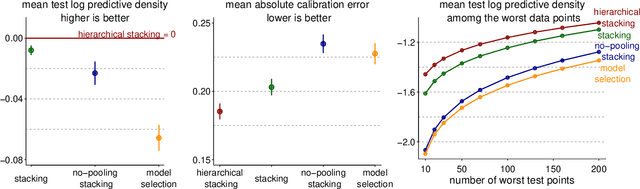
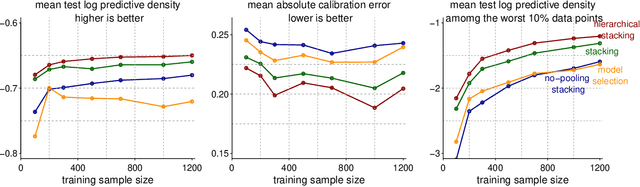
Stacking is a widely used model averaging technique that yields asymptotically optimal prediction among all linear averages. We show that stacking is most effective when the model predictive performance is heterogeneous in inputs, so that we can further improve the stacked mixture with a hierarchical model. With the input-varying yet partially-pooled model weights, hierarchical stacking improves average and conditional predictions. Our Bayesian formulation includes constant-weight (complete-pooling) stacking as a special case. We generalize to incorporate discrete and continuous inputs, other structured priors, and time-series and longitudinal data. We demonstrate on several applied problems.

Good practices for Bayesian Optimization of high dimensional structured spaces

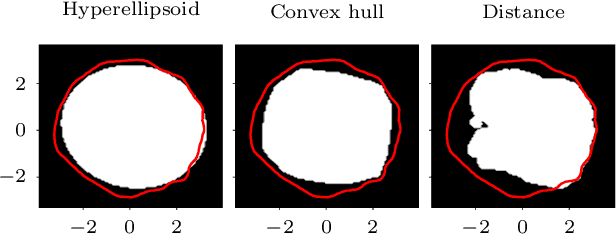
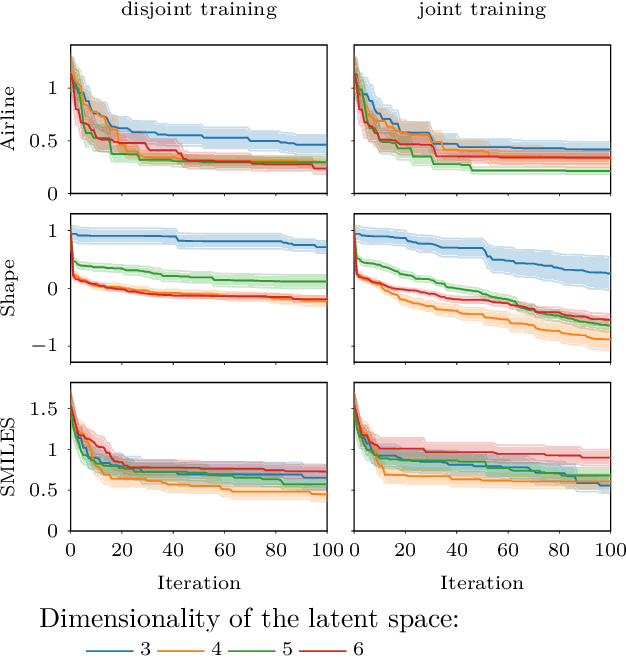
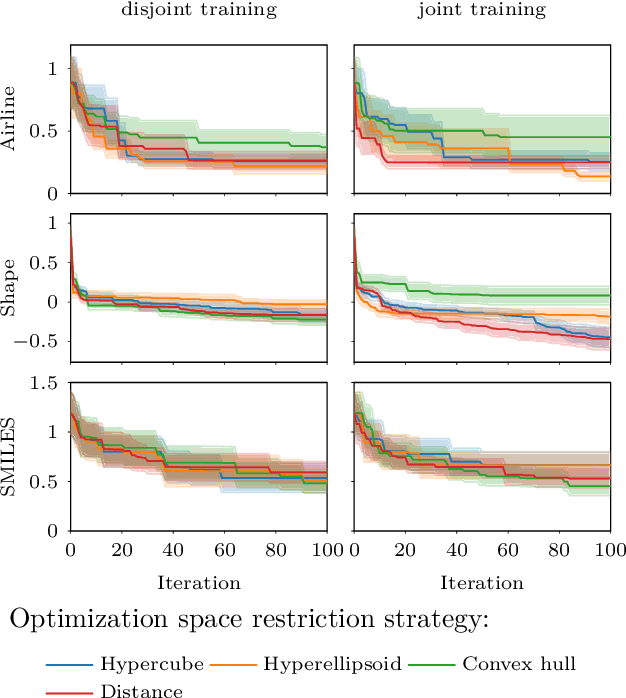
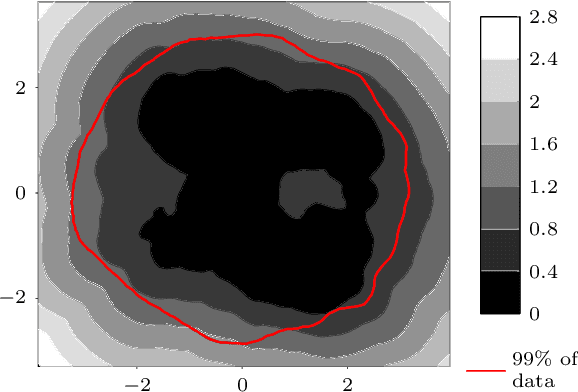
The increasing availability of structured but high dimensional data has opened new opportunities for optimization. One emerging and promising avenue is the exploration of unsupervised methods for projecting structured high dimensional data into low dimensional continuous representations, simplifying the optimization problem and enabling the application of traditional optimization methods. However, this line of research has been purely methodological with little connection to the needs of practitioners so far. In this paper, we study the effect of different search space design choices for performing Bayesian Optimization in high dimensional structured datasets. In particular, we analyse the influence of the dimensionality of the latent space, the role of the acquisition function and evaluate new methods to automatically define the optimization bounds in the latent space. Finally, based on experimental results using synthetic and real datasets, we provide recommendations for the practitioners.

Robust, Accurate Stochastic Optimization for Variational Inference

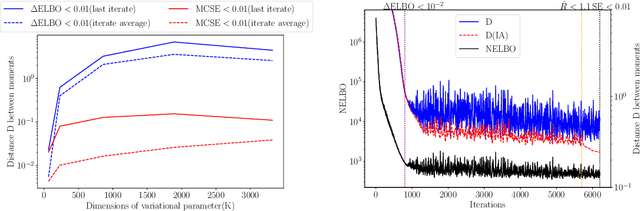
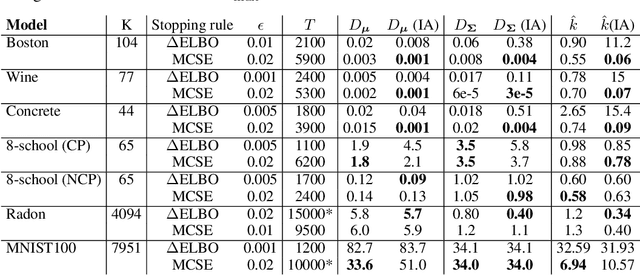
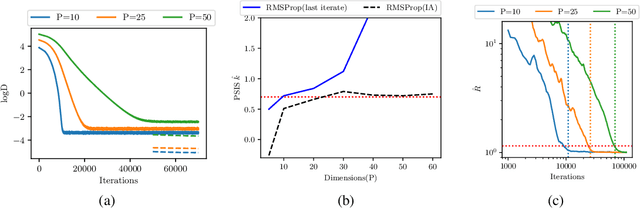
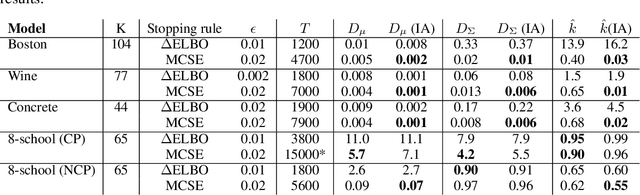
We consider the problem of fitting variational posterior approximations using stochastic optimization methods. The performance of these approximations depends on (1) how well the variational family matches the true posterior distribution,(2) the choice of divergence, and (3) the optimization of the variational objective. We show that even in the best-case scenario when the exact posterior belongs to the assumed variational family, common stochastic optimization methods lead to poor variational approximations if the problem dimension is moderately large. We also demonstrate that these methods are not robust across diverse model types. Motivated by these findings, we develop a more robust and accurate stochastic optimization framework by viewing the underlying optimization algorithm as producing a Markov chain. Our approach is theoretically motivated and includes a diagnostic for convergence and a novel stopping rule, both of which are robust to noisy evaluations of the objective function. We show empirically that the proposed framework works well on a diverse set of models: it can automatically detect stochastic optimization failure or inaccurate variational approximation

Stacking for Non-mixing Bayesian Computations: The Curse and Blessing of Multimodal Posteriors

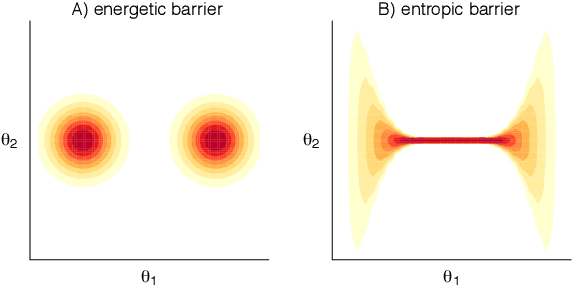
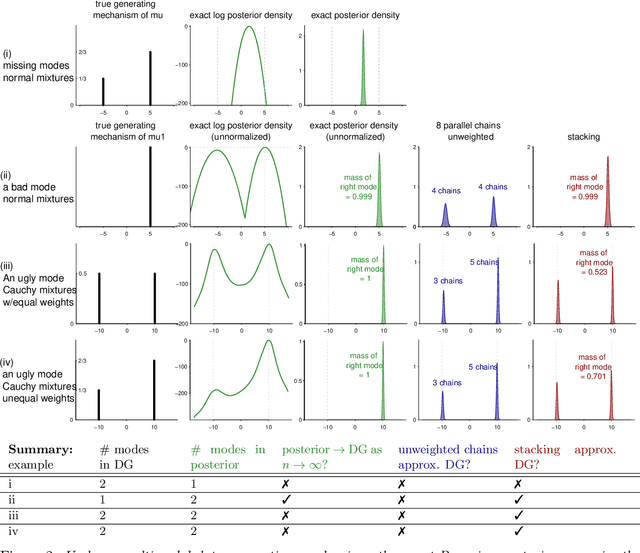
When working with multimodal Bayesian posterior distributions, Markov chain Monte Carlo (MCMC) algorithms can have difficulty moving between modes, and default variational or mode-based approximate inferences will understate posterior uncertainty. And, even if the most important modes can be found, it is difficult to evaluate their relative weights in the posterior. Here we propose an alternative approach, using parallel runs of MCMC, variational, or mode-based inference to hit as many modes or separated regions as possible, and then combining these using importance sampling based Bayesian stacking, a scalable method for constructing a weighted average of distributions so as to maximize cross-validated prediction utility. The result from stacking is not necessarily equivalent, even asymptotically, to fully Bayesian inference, but it serves many of the same goals. Under misspecified models, stacking can give better predictive performance than full Bayesian inference, hence the multimodality can be considered a blessing rather than a curse. We explore with an example where the stacked inference approximates the true data generating process from the misspecified model, an example of inconsistent inference, and non-mixing samplers. We elaborate the practical implantation in the context of latent Dirichlet allocation, Gaussian process regression, hierarchical model, variational inference in horseshoe regression, and neural networks.

Group Heterogeneity Assessment for Multilevel Models

Many data sets contain an inherent multilevel structure, for example, because of repeated measurements of the same observational units. Taking this structure into account is critical for the accuracy and calibration of any statistical analysis performed on such data. However, the large number of possible model configurations hinders the use of multilevel models in practice. In this work, we propose a flexible framework for efficiently assessing differences between the levels of given grouping variables in the data. The assessed group heterogeneity is valuable in choosing the relevant group coefficients to consider in a multilevel model. Our empirical evaluations demonstrate that the framework can reliably identify relevant multilevel components in both simulated and real data sets.