BayesFlow 2.0: Multi-Backend Amortized Bayesian Inference in Python

Modern Bayesian inference involves a mixture of computational methods for estimating, validating, and drawing conclusions from probabilistic models as part of principled workflows. An overarching motif of many Bayesian methods is that they are relatively slow, which often becomes prohibitive when fitting complex models to large data sets. Amortized Bayesian inference (ABI) offers a path to solving the computational challenges of Bayes. ABI trains neural networks on model simulations, rewarding users with rapid inference of any model-implied quantity, such as point estimates, likelihoods, or full posterior distributions. In this work, we present the Python library BayesFlow, Version 2.0, for general-purpose ABI. Along with direct posterior, likelihood, and ratio estimation, the software includes support for multiple popular deep learning backends, a rich collection of generative networks for sampling and density estimation, complete customization and high-level interfaces, as well as new capabilities for hyperparameter optimization, design optimization, and hierarchical modeling. Using a case study on dynamical system parameter estimation, combined with comparisons to similar software, we show that our streamlined, user-friendly workflow has strong potential to support broad adoption.

Enhancing Sentiment Classification and Irony Detection in Large Language Models through Advanced Prompt Engineering Techniques

This study investigates the use of prompt engineering to enhance large language models (LLMs), specifically GPT-4o-mini and gemini-1.5-flash, in sentiment analysis tasks. It evaluates advanced prompting techniques like few-shot learning, chain-of-thought prompting, and self-consistency against a baseline. Key tasks include sentiment classification, aspect-based sentiment analysis, and detecting subtle nuances such as irony. The research details the theoretical background, datasets, and methods used, assessing performance of LLMs as measured by accuracy, recall, precision, and F1 score. Findings reveal that advanced prompting significantly improves sentiment analysis, with the few-shot approach excelling in GPT-4o-mini and chain-of-thought prompting boosting irony detection in gemini-1.5-flash by up to 46%. Thus, while advanced prompting techniques overall improve performance, the fact that few-shot prompting works best for GPT-4o-mini and chain-of-thought excels in gemini-1.5-flash for irony detection suggests that prompting strategies must be tailored to both the model and the task. This highlights the importance of aligning prompt design with both the LLM's architecture and the semantic complexity of the task.

Posterior SBC: Simulation-Based Calibration Checking Conditional on Data

Simulation-based calibration checking (SBC) refers to the validation of an inference algorithm and model implementation through repeated inference on data simulated from a generative model. In the original and commonly used approach, the generative model uses parameters drawn from the prior, and thus the approach is testing whether the inference works for simulated data generated with parameter values plausible under that prior. This approach is natural and desirable when we want to test whether the inference works for a wide range of datasets we might observe. However, after observing data, we are interested in answering whether the inference works conditional on that particular data. In this paper, we propose posterior SBC and demonstrate how it can be used to validate the inference conditionally on observed data. We illustrate the utility of posterior SBC in three case studies: (1) A simple multilevel model; (2) a model that is governed by differential equations; and (3) a joint integrative neuroscience model which is approximated via amortized Bayesian inference with neural networks.

Amortized Bayesian Workflow (Extended Abstract)

Bayesian inference often faces a trade-off between computational speed and sampling accuracy. We propose an adaptive workflow that integrates rapid amortized inference with gold-standard MCMC techniques to achieve both speed and accuracy when performing inference on many observed datasets. Our approach uses principled diagnostics to guide the choice of inference method for each dataset, moving along the Pareto front from fast amortized sampling to slower but guaranteed-accurate MCMC when necessary. By reusing computations across steps, our workflow creates synergies between amortized and MCMC-based inference. We demonstrate the effectiveness of this integrated approach on a generalized extreme value task with 1000 observed data sets, showing 90x time efficiency gains while maintaining high posterior quality.

Amortized Bayesian Multilevel Models

Multilevel models (MLMs) are a central building block of the Bayesian workflow. They enable joint, interpretable modeling of data across hierarchical levels and provide a fully probabilistic quantification of uncertainty. Despite their well-recognized advantages, MLMs pose significant computational challenges, often rendering their estimation and evaluation intractable within reasonable time constraints. Recent advances in simulation-based inference offer promising solutions for addressing complex probabilistic models using deep generative networks. However, the utility and reliability of deep learning methods for estimating Bayesian MLMs remains largely unexplored, especially when compared with gold-standard samplers. To this end, we explore a family of neural network architectures that leverage the probabilistic factorization of multilevel models to facilitate efficient neural network training and subsequent near-instant posterior inference on unseen data sets. We test our method on several real-world case studies and provide comprehensive comparisons to Stan as a gold-standard method where possible. Finally, we provide an open-source implementation of our methods to stimulate further research in the nascent field of amortized Bayesian inference.

Detecting Model Misspecification in Amortized Bayesian Inference with Neural Networks: An Extended Investigation

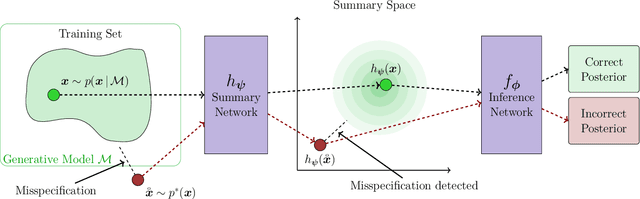
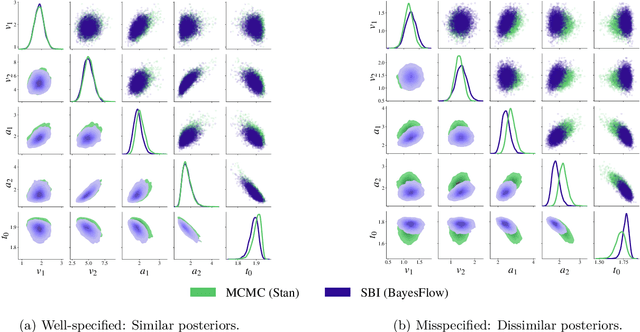
Recent advances in probabilistic deep learning enable efficient amortized Bayesian inference in settings where the likelihood function is only implicitly defined by a simulation program (simulation-based inference; SBI). But how faithful is such inference if the simulation represents reality somewhat inaccurately, that is, if the true system behavior at test time deviates from the one seen during training? We conceptualize the types of such model misspecification arising in SBI and systematically investigate how the performance of neural posterior approximators gradually deteriorates as a consequence, making inference results less and less trustworthy. To notify users about this problem, we propose a new misspecification measure that can be trained in an unsupervised fashion (i.e., without training data from the true distribution) and reliably detects model misspecification at test time. Our experiments clearly demonstrate the utility of our new measure both on toy examples with an analytical ground-truth and on representative scientific tasks in cell biology, cognitive decision making, disease outbreak dynamics, and computer vision. We show how the proposed misspecification test warns users about suspicious outputs, raises an alarm when predictions are not trustworthy, and guides model designers in their search for better simulators.

Consistency Models for Scalable and Fast Simulation-Based Inference

Simulation-based inference (SBI) is constantly in search of more expressive algorithms for accurately inferring the parameters of complex models from noisy data. We present consistency models for neural posterior estimation (CMPE), a new free-form conditional sampler for scalable, fast, and amortized SBI with generative neural networks. CMPE combines the advantages of normalizing flows and flow matching methods into a single generative architecture: It essentially distills a continuous probability flow and enables rapid few-shot inference with an unconstrained architecture that can be tailored to the structure of the estimation problem. Our empirical evaluation demonstrates that CMPE not only outperforms current state-of-the-art algorithms on three hard low-dimensional problems, but also achieves competitive performance in a high-dimensional Bayesian denoising experiment and in estimating a computationally demanding multi-scale model of tumor spheroid growth.

Fuse It or Lose It: Deep Fusion for Multimodal Simulation-Based Inference

We present multimodal neural posterior estimation (MultiNPE), a method to integrate heterogeneous data from different sources in simulation-based inference with neural networks. Inspired by advances in attention-based deep fusion learning, it empowers researchers to analyze data from different domains and infer the parameters of complex mathematical models with increased accuracy. We formulate different multimodal fusion approaches for MultiNPE (early, late, and hybrid) and evaluate their performance in three challenging numerical experiments. MultiNPE not only outperforms na\"ive baselines on a benchmark model, but also achieves superior inference on representative scientific models from neuroscience and cardiology. In addition, we systematically investigate the impact of partially missing data on the different fusion strategies. Across our different experiments, late and hybrid fusion techniques emerge as the methods of choice for practical applications of multimodal simulation-based inference.

Sensitivity-Aware Amortized Bayesian Inference

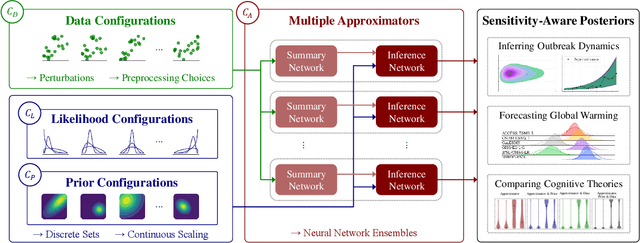
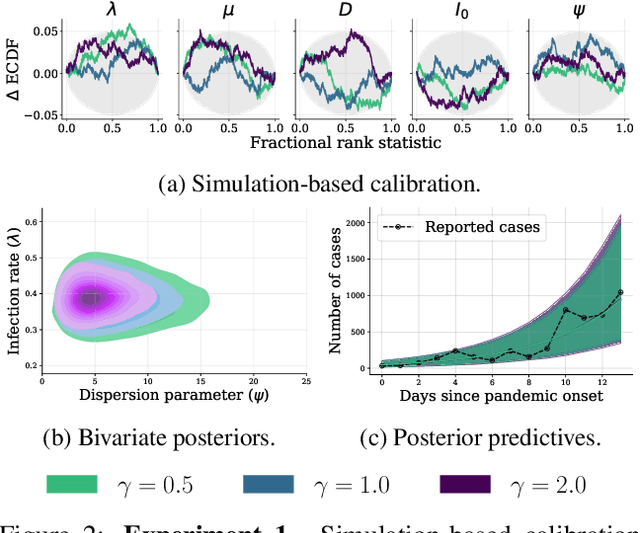
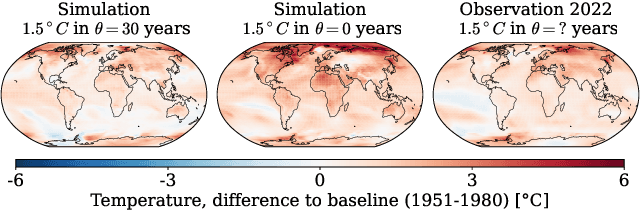
Bayesian inference is a powerful framework for making probabilistic inferences and decisions under uncertainty. Fundamental choices in modern Bayesian workflows concern the specification of the likelihood function and prior distributions, the posterior approximator, and the data. Each choice can significantly influence model-based inference and subsequent decisions, thereby necessitating sensitivity analysis. In this work, we propose a multifaceted approach to integrate sensitivity analyses into amortized Bayesian inference (ABI, i.e., simulation-based inference with neural networks). First, we utilize weight sharing to encode the structural similarities between alternative likelihood and prior specifications in the training process with minimal computational overhead. Second, we leverage the rapid inference of neural networks to assess sensitivity to various data perturbations or pre-processing procedures. In contrast to most other Bayesian approaches, both steps circumvent the costly bottleneck of refitting the model(s) for each choice of likelihood, prior, or dataset. Finally, we propose to use neural network ensembles to evaluate variation in results induced by unreliable approximation on unseen data. We demonstrate the effectiveness of our method in applied modeling problems, ranging from the estimation of disease outbreak dynamics and global warming thresholds to the comparison of human decision-making models. Our experiments showcase how our approach enables practitioners to effectively unveil hidden relationships between modeling choices and inferential conclusions.

Leveraging Self-Consistency for Data-Efficient Amortized Bayesian Inference

We propose a method to improve the efficiency and accuracy of amortized Bayesian inference (ABI) by leveraging universal symmetries in the probabilistic joint model $p(\theta, y)$ of parameters $\theta$ and data $y$. In a nutshell, we invert Bayes' theorem and estimate the marginal likelihood based on approximate representations of the joint model. Upon perfect approximation, the marginal likelihood is constant across all parameter values by definition. However, approximation error leads to undesirable variance in the marginal likelihood estimates across different parameter values. We formulate violations of this symmetry as a loss function to accelerate the learning dynamics of conditional neural density estimators. We apply our method to a bimodal toy problem with an explicit likelihood (likelihood-based) and a realistic model with an implicit likelihood (simulation-based).