Does Unsupervised Domain Adaptation Improve the Robustness of Amortized Bayesian Inference? A Systematic Evaluation

Neural networks are fragile when confronted with data that significantly deviates from their training distribution. This is true in particular for simulation-based inference methods, such as neural amortized Bayesian inference (ABI), where models trained on simulated data are deployed on noisy real-world observations. Recent robust approaches employ unsupervised domain adaptation (UDA) to match the embedding spaces of simulated and observed data. However, the lack of comprehensive evaluations across different domain mismatches raises concerns about the reliability in high-stakes applications. We address this gap by systematically testing UDA approaches across a wide range of misspecification scenarios in both a controlled and a high-dimensional benchmark. We demonstrate that aligning summary spaces between domains effectively mitigates the impact of unmodeled phenomena or noise. However, the same alignment mechanism can lead to failures under prior misspecifications - a critical finding with practical consequences. Our results underscore the need for careful consideration of misspecification types when using UDA techniques to increase the robustness of ABI in practice.

Consistency Models for Scalable and Fast Simulation-Based Inference

Simulation-based inference (SBI) is constantly in search of more expressive algorithms for accurately inferring the parameters of complex models from noisy data. We present consistency models for neural posterior estimation (CMPE), a new free-form conditional sampler for scalable, fast, and amortized SBI with generative neural networks. CMPE combines the advantages of normalizing flows and flow matching methods into a single generative architecture: It essentially distills a continuous probability flow and enables rapid few-shot inference with an unconstrained architecture that can be tailored to the structure of the estimation problem. Our empirical evaluation demonstrates that CMPE not only outperforms current state-of-the-art algorithms on three hard low-dimensional problems, but also achieves competitive performance in a high-dimensional Bayesian denoising experiment and in estimating a computationally demanding multi-scale model of tumor spheroid growth.

BayesFlow: Amortized Bayesian Workflows With Neural Networks

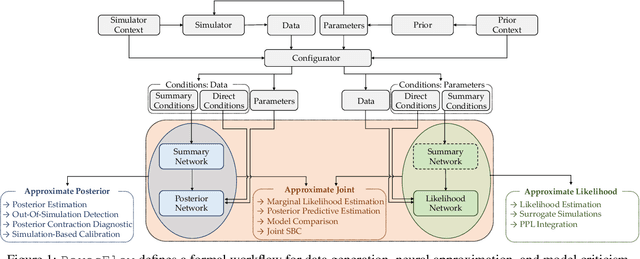
Modern Bayesian inference involves a mixture of computational techniques for estimating, validating, and drawing conclusions from probabilistic models as part of principled workflows for data analysis. Typical problems in Bayesian workflows are the approximation of intractable posterior distributions for diverse model types and the comparison of competing models of the same process in terms of their complexity and predictive performance. This manuscript introduces the Python library BayesFlow for simulation-based training of established neural network architectures for amortized data compression and inference. Amortized Bayesian inference, as implemented in BayesFlow, enables users to train custom neural networks on model simulations and re-use these networks for any subsequent application of the models. Since the trained networks can perform inference almost instantaneously, the upfront neural network training is quickly amortized.

JANA: Jointly Amortized Neural Approximation of Complex Bayesian Models

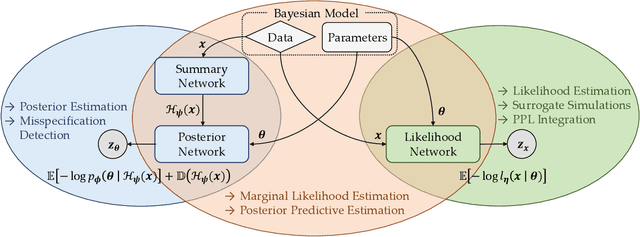
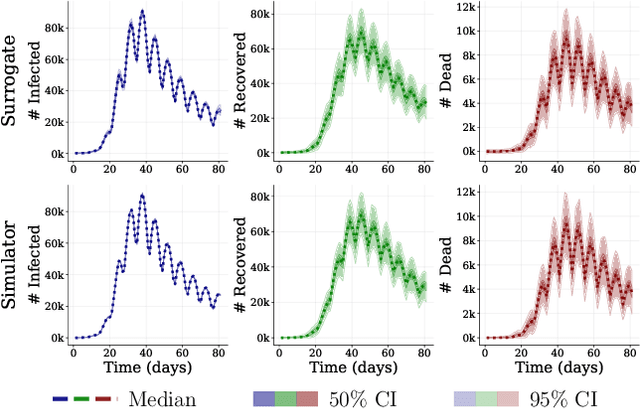
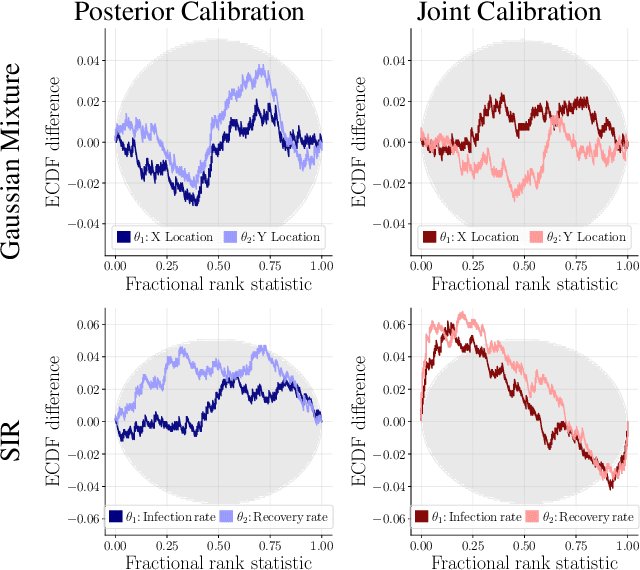
This work proposes ''jointly amortized neural approximation'' (JANA) of intractable likelihood functions and posterior densities arising in Bayesian surrogate modeling and simulation-based inference. We train three complementary networks in an end-to-end fashion: 1) a summary network to compress individual data points, sets, or time series into informative embedding vectors; 2) a posterior network to learn an amortized approximate posterior; and 3) a likelihood network to learn an amortized approximate likelihood. Their interaction opens a new route to amortized marginal likelihood and posterior predictive estimation -- two important ingredients of Bayesian workflows that are often too expensive for standard methods. We benchmark the fidelity of JANA on a variety of simulation models against state-of-the-art Bayesian methods and propose a powerful and interpretable diagnostic for joint calibration. In addition, we investigate the ability of recurrent likelihood networks to emulate complex time series models without resorting to hand-crafted summary statistics.