Does Unsupervised Domain Adaptation Improve the Robustness of Amortized Bayesian Inference? A Systematic Evaluation

Neural networks are fragile when confronted with data that significantly deviates from their training distribution. This is true in particular for simulation-based inference methods, such as neural amortized Bayesian inference (ABI), where models trained on simulated data are deployed on noisy real-world observations. Recent robust approaches employ unsupervised domain adaptation (UDA) to match the embedding spaces of simulated and observed data. However, the lack of comprehensive evaluations across different domain mismatches raises concerns about the reliability in high-stakes applications. We address this gap by systematically testing UDA approaches across a wide range of misspecification scenarios in both a controlled and a high-dimensional benchmark. We demonstrate that aligning summary spaces between domains effectively mitigates the impact of unmodeled phenomena or noise. However, the same alignment mechanism can lead to failures under prior misspecifications - a critical finding with practical consequences. Our results underscore the need for careful consideration of misspecification types when using UDA techniques to increase the robustness of ABI in practice.

Neural Superstatistics: A Bayesian Method for Estimating Dynamic Models of Cognition

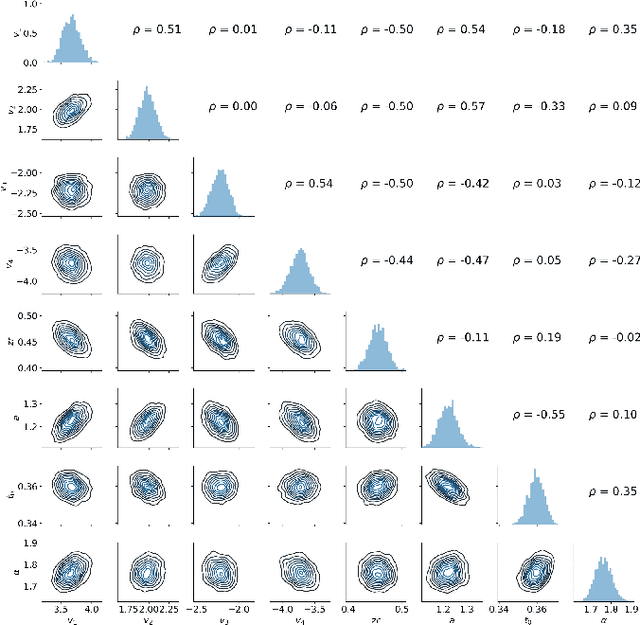
Mathematical models of cognition are often memoryless and ignore potential fluctuations of their parameters. However, human cognition is inherently dynamic, regardless of the reference time scale. Thus, we propose to augment mechanistic cognitive models with a temporal dimension and estimate the resulting dynamics from a superstatistics perspective. In its simplest form, such a model entails a hierarchy between a low-level observation model and a high-level transition model. The observation model describes the local behavior of a system, and the transition model specifies how the parameters of the observation model evolve over time. To overcome the estimation challenges resulting from the complexity of superstatistical models, we develop and validate a simulation-based deep learning method for Bayesian inference, which can recover both time-varying and time-invariant parameters. We first benchmark our method against two existing frameworks capable of estimating time-varying parameters. We then apply our method to fit a dynamic version of the diffusion decision model to long time series of human response times data. Our results show that the deep learning approach is very efficient in capturing the temporal dynamics of the model. Furthermore, we show that the erroneous assumption of static or homogeneous parameters will hide important temporal information.

Amortized Bayesian Inference for Models of Cognition

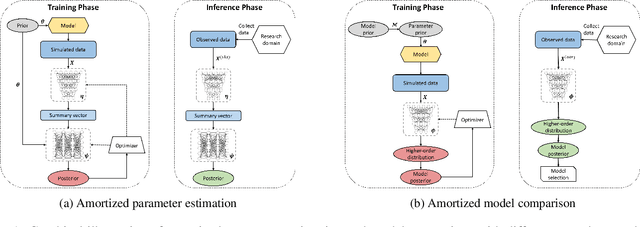
As models of cognition grow in complexity and number of parameters, Bayesian inference with standard methods can become intractable, especially when the data-generating model is of unknown analytic form. Recent advances in simulation-based inference using specialized neural network architectures circumvent many previous problems of approximate Bayesian computation. Moreover, due to the properties of these special neural network estimators, the effort of training the networks via simulations amortizes over subsequent evaluations which can re-use the same network for multiple datasets and across multiple researchers. However, these methods have been largely underutilized in cognitive science and psychology so far, even though they are well suited for tackling a wide variety of modeling problems. With this work, we provide a general introduction to amortized Bayesian parameter estimation and model comparison and demonstrate the applicability of the proposed methods on a well-known class of intractable response-time models.

Amortized Bayesian model comparison with evidential deep learning

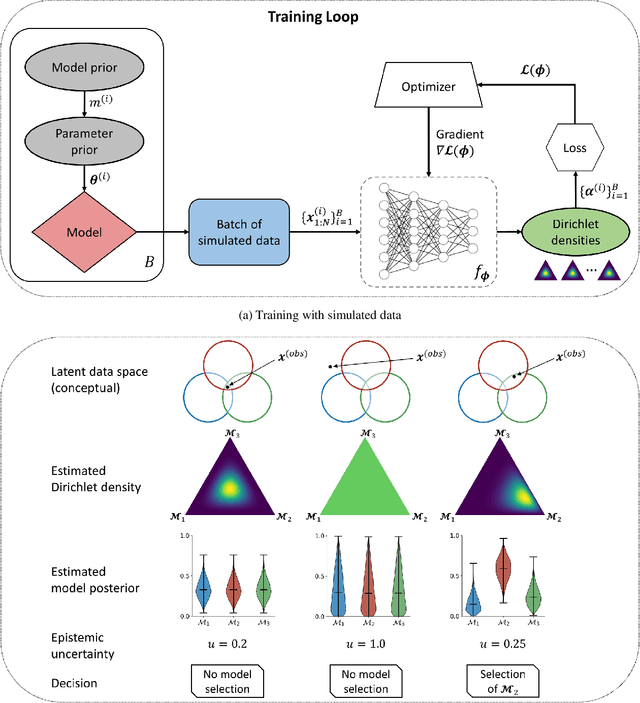
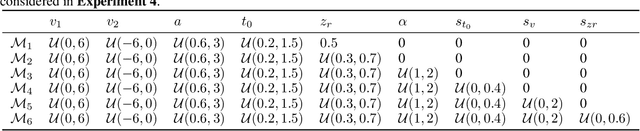
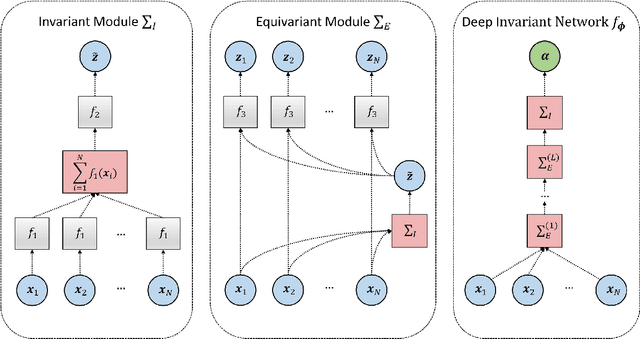
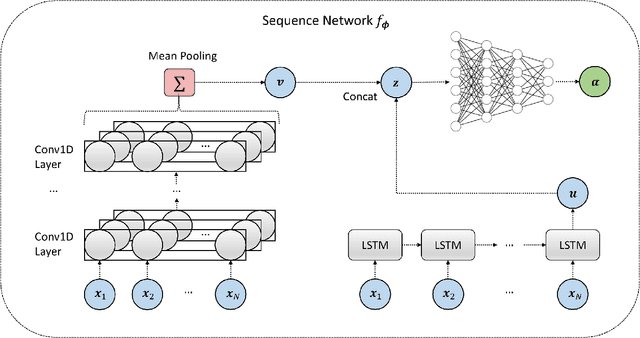
Comparing competing mathematical models of complex natural processes is a shared goal among many branches of science. The Bayesian probabilistic framework offers a principled way to perform model comparison and extract useful metrics for guiding decisions. However, many interesting models are intractable with standard Bayesian methods, as they lack a closed-form likelihood function or the likelihood is computationally too expensive to evaluate. With this work, we propose a novel method for performing Bayesian model comparison using specialized deep learning architectures. Our method is purely simulation-based and circumvents the step of explicitly fitting all alternative models under consideration to each observed dataset. Moreover, it involves no hand-crafted summary statistics of the data and is designed to amortize the cost of simulation over multiple models and observable datasets. This makes the method applicable in scenarios where model fit needs to be assessed for a large number of datasets, so that per-dataset inference is practically infeasible. Finally, we propose a novel way to measure epistemic uncertainty in model comparison problems. We argue that this measure of epistemic uncertainty provides a unique proxy to quantify absolute evidence even in a framework which assumes that the true data-generating model is within a finite set of candidate models.