Amortized Bayesian model comparison with evidential deep learning

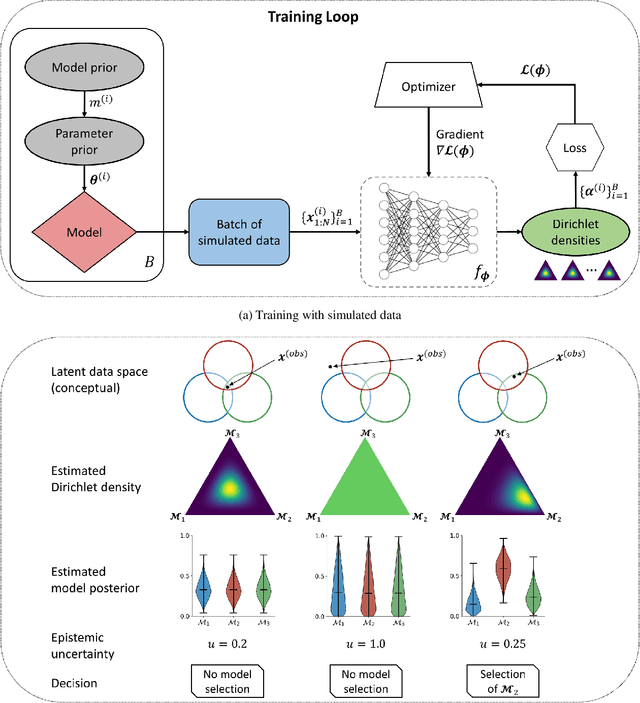
Comparing competing mathematical models of complex natural processes is a shared goal among many branches of science. The Bayesian probabilistic framework offers a principled way to perform model comparison and extract useful metrics for guiding decisions. However, many interesting models are intractable with standard Bayesian methods, as they lack a closed-form likelihood function or the likelihood is computationally too expensive to evaluate. With this work, we propose a novel method for performing Bayesian model comparison using specialized deep learning architectures. Our method is purely simulation-based and circumvents the step of explicitly fitting all alternative models under consideration to each observed dataset. Moreover, it involves no hand-crafted summary statistics of the data and is designed to amortize the cost of simulation over multiple models and observable datasets. This makes the method applicable in scenarios where model fit needs to be assessed for a large number of datasets, so that per-dataset inference is practically infeasible. Finally, we propose a novel way to measure epistemic uncertainty in model comparison problems. We argue that this measure of epistemic uncertainty provides a unique proxy to quantify absolute evidence even in a framework which assumes that the true data-generating model is within a finite set of candidate models.

BayesFlow: Learning complex stochastic models with invertible neural networks

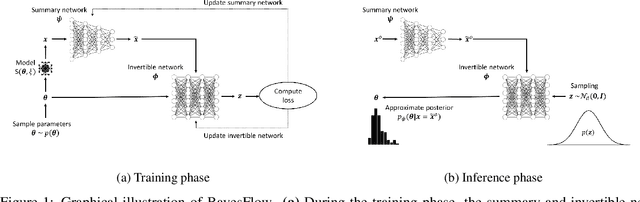
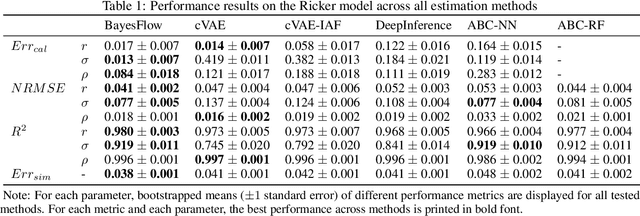
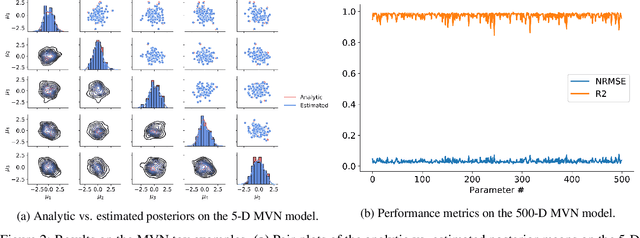
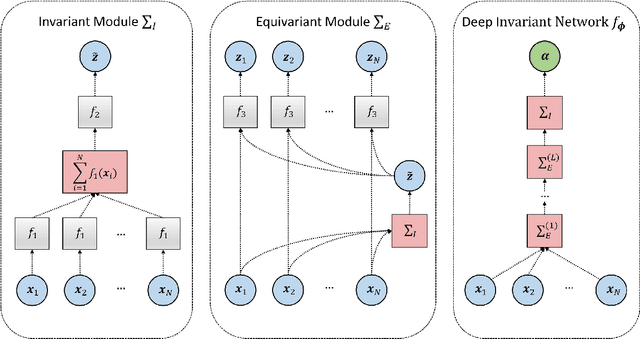
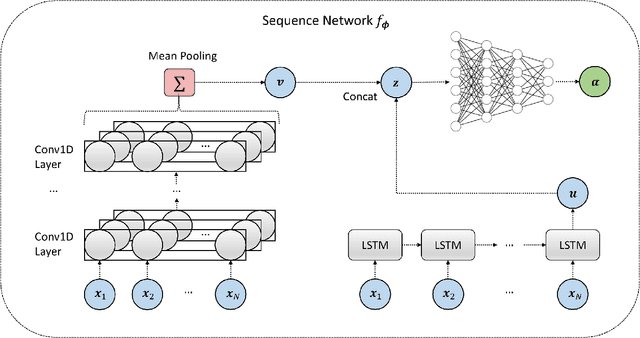
Estimating the parameters of mathematical models is a common problem in almost all branches of science. However, this problem can prove notably difficult when processes and model descriptions become increasingly complex and an explicit likelihood function is not available. With this work, we propose a novel method for globally amortized Bayesian inference based on invertible neural networks which we call BayesFlow. The method uses simulation to learn a global estimator for the probabilistic mapping from observed data to underlying model parameters. A neural network pre-trained in this way can then, without additional training or optimization, infer full posteriors on arbitrary many real data sets involving the same model family. In addition, our method incorporates a summary network trained to embed the observed data into maximally informative summary statistics. Learning summary statistics from data makes the method applicable to modeling scenarios where standard inference techniques with hand-crafted summary statistics fail. We demonstrate the utility of BayesFlow on challenging intractable models from population dynamics, epidemiology, cognitive science and ecology. We argue that BayesFlow provides a general framework for building reusable Bayesian parameter estimation machines for any process model from which data can be simulated.