Simulation-based inference for stochastic nonlinear mixed-effects models with applications in systems biology

The analysis of data from multiple experiments, such as observations of several individuals, is commonly approached using mixed-effects models, which account for variation between individuals through hierarchical representations. This makes mixed-effects models widely applied in fields such as biology, pharmacokinetics, and sociology. In this work, we propose a novel methodology for scalable Bayesian inference in hierarchical mixed-effects models. Our framework first constructs amortized approximations of the likelihood and the posterior distribution, which are then rapidly refined for each individual dataset, to ultimately approximate the parameters posterior across many individuals. The framework is easily trainable, as it uses mixtures of experts but without neural networks, leading to parsimonious yet expressive surrogate models of the likelihood and the posterior. We demonstrate the effectiveness of our methodology using challenging stochastic models, such as mixed-effects stochastic differential equations emerging in systems biology-driven problems. However, the approach is broadly applicable and can accommodate both stochastic and deterministic models. We show that our approach can seamlessly handle inference for many parameters. Additionally, we applied our method to a real-data case study of mRNA transfection. When compared to exact pseudomarginal Bayesian inference, our approach proved to be both fast and competitive in terms of statistical accuracy.

Fast, accurate and lightweight sequential simulation-based inference using Gaussian locally linear mappings

Bayesian inference for complex models with an intractable likelihood can be tackled using algorithms performing many calls to computer simulators. These approaches are collectively known as "simulation-based inference" (SBI). Recent SBI methods have made use of neural networks (NN) to provide approximate, yet expressive constructs for the unavailable likelihood function and the posterior distribution. However, they do not generally achieve an optimal trade-off between accuracy and computational demand. In this work, we propose an alternative that provides both approximations to the likelihood and the posterior distribution, using structured mixtures of probability distributions. Our approach produces accurate posterior inference when compared to state-of-the-art NN-based SBI methods, while exhibiting a much smaller computational footprint. We illustrate our results on several benchmark models from the SBI literature.

JANA: Jointly Amortized Neural Approximation of Complex Bayesian Models

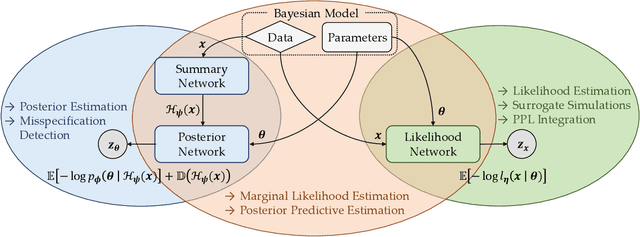
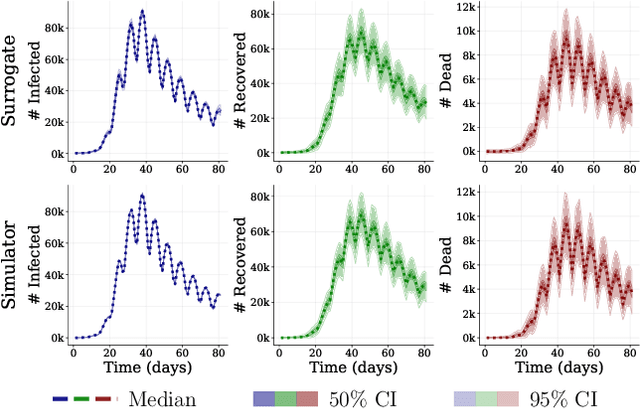
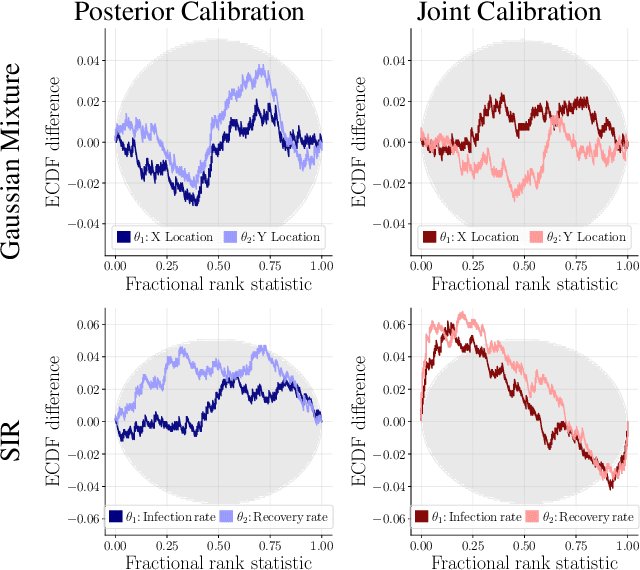
This work proposes ''jointly amortized neural approximation'' (JANA) of intractable likelihood functions and posterior densities arising in Bayesian surrogate modeling and simulation-based inference. We train three complementary networks in an end-to-end fashion: 1) a summary network to compress individual data points, sets, or time series into informative embedding vectors; 2) a posterior network to learn an amortized approximate posterior; and 3) a likelihood network to learn an amortized approximate likelihood. Their interaction opens a new route to amortized marginal likelihood and posterior predictive estimation -- two important ingredients of Bayesian workflows that are often too expensive for standard methods. We benchmark the fidelity of JANA on a variety of simulation models against state-of-the-art Bayesian methods and propose a powerful and interpretable diagnostic for joint calibration. In addition, we investigate the ability of recurrent likelihood networks to emulate complex time series models without resorting to hand-crafted summary statistics.

Sequential Neural Posterior and Likelihood Approximation

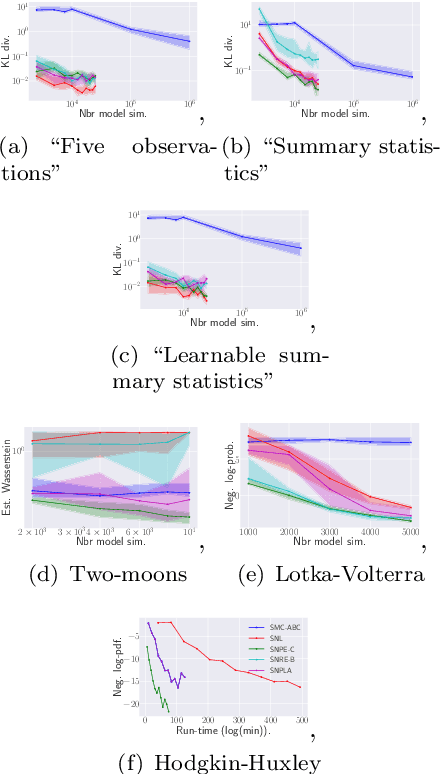
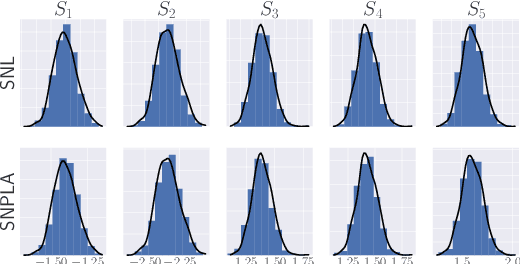
We introduce the sequential neural posterior and likelihood approximation (SNPLA) algorithm. SNPLA is a normalizing flows-based algorithm for inference in implicit models. Thus, SNPLA is a simulation-based inference method that only requires simulations from a generative model. Compared to similar methods, the main advantage of SNPLA is that our method jointly learns both the posterior and the likelihood. SNPLA completely avoid Markov chain Monte Carlo sampling and correction-steps of the parameter proposal function that are introduced in similar methods, but that can be numerically unstable or restrictive. Over four experiments, we show that SNPLA performs competitively when utilizing the same number of model simulations as used in other methods, even though the inference problem for SNPLA is more complex due to the joint learning of posterior and likelihood function.

Partially Exchangeable Networks and Architectures for Learning Summary Statistics in Approximate Bayesian Computation

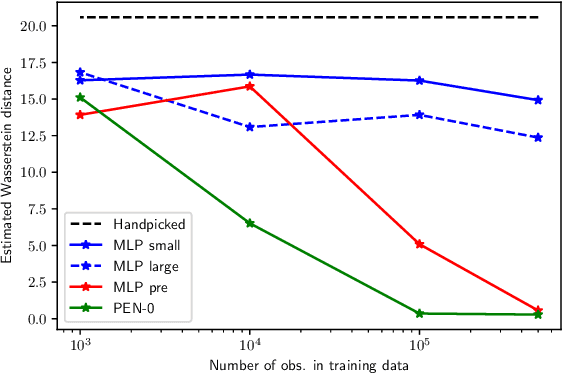
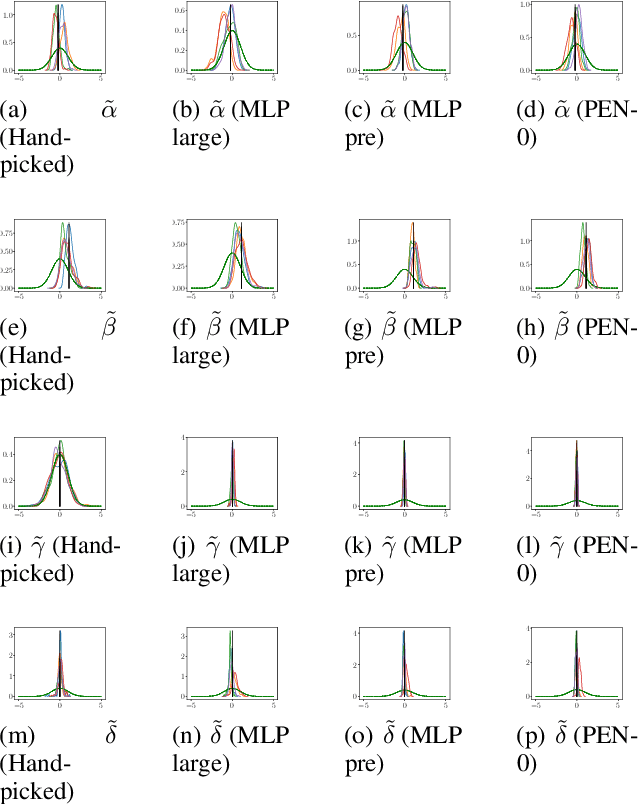
We present a novel family of deep neural architectures, named partially exchangeable networks (PENs) that leverage probabilistic symmetries. By design, PENs are invariant to block-switch transformations, which characterize the partial exchangeability properties of conditionally Markovian processes. Moreover, we show that any block-switch invariant function has a PEN-like representation. The DeepSets architecture is a special case of PEN and we can therefore also target fully exchangeable data. We employ PENs to learn summary statistics in approximate Bayesian computation (ABC). When comparing PENs to previous deep learning methods for learning summary statistics, our results are highly competitive, both considering time series and static models. Indeed, PENs provide more reliable posterior samples even when using less training data.