Routing on the Stiefel Manifold: When Does Adaptive Subspace Selection Help for Cross-Domain EEG Decoding?

Cross-domain EEG decoding remains challenging despite advances in Riemannian deep learning: covariance matrices from different subjects occupy systematically distinct regions of the SPD manifold, yet existing domain adaptation methods either require target-domain calibration data or learn subject-specific components that cannot generalise across domains. We propose dynamic Stiefel routing: a pool of $K$ expert projection filters on the Stiefel manifold, each specialised for a different region of the SPD manifold, with each input covariance routed to the most appropriate filter via cross-attention, adapting the subspace projection per sample. A central finding is that this approach, implemented naively, provably collapses to ensemble averaging: when routing weights are uniform, the adaptive filter reduces exactly to an equal-contribution combination of experts, indistinguishable from a single fixed filter. Three structural properties break this degeneracy: a symmetric anchor $W_{\mathrm{base}} \in \mathrm{St}(n,k)$ that removes proximity bias among experts; a frozen domain-discriminative query encoder that decouples routing from task optimisation; and a decoupled key alignment loss that trains expert keys toward stable domain attractors. Together they produce the first genuinely committed and domain-structured routing on SPD manifolds, with consistent gains across three datasets: balanced accuracy improves from $0.773\to 0.823$, $0.757\to 0.809$, and $0.801\to 0.839$, with the alignment strategy determined automatically by a single data-driven rule and no dataset-specific hyperparameter search.

$\textit{BlockFormer}$ : Transformer-based inference from interaction maps

Inference from interaction maps, such as centromere identification from genome-wide chromosome conformation capture techniques -- notably Hi-C -- can be formulated as a generic inverse problem: infer a set of parameters given a map summarizing pairwise interactions between entities through blocks of variable numbers and sizes. In this work, we introduce a data-driven approach that leverages shared structure between these maps, such as global alignment between localized patterns, while handling the variability in number and size of entities arising in real-world data. Our approach relies on a transformer architecture capable of handling such variability and a custom simulator to generate abundant, yet computationally cheap synthetic data for training. Applied to the problem of centromere localization, the method accurately recovers their genomic positions across a wide range of species of various genome sizes.

Theoretical guidelines for annealed Langevin dynamics in compositional simulation-based inference

Compositional score-based approaches to simulation-based inference (SBI) approximate the posterior over a shared parameter given $n$ independent observations by aggregating individually learned posterior scores: currently, there are two main propositions of such methods (Geffner et al. (2023), Linhart et al. (2026)). As the resulting composite score does not correspond to the score of any distribution along the forward diffusion path of the true multi-observation posterior, sampling from it via a reverse SDE leads to an irreducible bias. Annealed Langevin dynamics provides a principled alternative: it treats the composite score as the genuine score of a sequence of tractable bridging densities and samples from them in succession. When properly tuned, it could lead to a controllable bias. However, its hyperparameters, namely step sizes, the number of steps per level, and the number of annealing levels, have so far been chosen empirically. We derive Wasserstein bounds for annealed Langevin with approximate scores and translate them into explicit decision rules for these hyperparameters that guarantee a prescribed sampling accuracy, while highlighting different theoretical aspects of each composite score formulation. In the Gaussian setting, we obtain closed-form expressions for all relevant quantities and prove that the bridging densities of Linhart et al. (2026) consistently admit larger step sizes and require fewer total Langevin steps than those of Geffner et al. (2023). Furthermore, we show empirically that the tuning obtained in the Gaussian setting generalizes to more complex problems, thus providing a well-understood and theoretically grounded starting point for practitioners using compositional score-based approaches.

Benchmarking Tabular Foundation Models for Conditional Density Estimation in Regression

Conditional density estimation (CDE) - recovering the full conditional distribution of a response given tabular covariates - is essential in settings with heteroscedasticity, multimodality, or asymmetric uncertainty. Recent tabular foundation models, such as TabPFN and TabICL, naturally produce predictive distributions, but their effectiveness as general-purpose CDE methods has not been systematically evaluated, unlike their performance for point prediction, which is well studied. We benchmark three tabular foundation model variants against a diverse set of parametric, tree-based, and neural CDE baselines on 39 real-world datasets, across training sizes from 50 to 20,000, using six metrics covering density accuracy, calibration, and computation time. Across all sample sizes, foundation models achieve the best CDE loss, log-likelihood, and CRPS on the large majority of datasets tested. Calibration is competitive at small sample sizes but, for some metrics and datasets, lags behind task-specific neural baselines at larger sample sizes, suggesting that post-hoc recalibration may be a valuable complement. In a photometric redshift case study using SDSS DR18, TabPFN exposed to 50,000 training galaxies outperforms all baselines trained on the full 500,000-galaxy dataset. Taken together, these results establish tabular foundation models as strong off-the-shelf conditional density estimators.

CP4SBI: Local Conformal Calibration of Credible Sets in Simulation-Based Inference

Current experimental scientists have been increasingly relying on simulation-based inference (SBI) to invert complex non-linear models with intractable likelihoods. However, posterior approximations obtained with SBI are often miscalibrated, causing credible regions to undercover true parameters. We develop $\texttt{CP4SBI}$, a model-agnostic conformal calibration framework that constructs credible sets with local Bayesian coverage. Our two proposed variants, namely local calibration via regression trees and CDF-based calibration, enable finite-sample local coverage guarantees for any scoring function, including HPD, symmetric, and quantile-based regions. Experiments on widely used SBI benchmarks demonstrate that our approach improves the quality of uncertainty quantification for neural posterior estimators using both normalizing flows and score-diffusion modeling.

Diffusion posterior sampling for simulation-based inference in tall data settings

Determining which parameters of a non-linear model could best describe a set of experimental data is a fundamental problem in science and it has gained much traction lately with the rise of complex large-scale simulators (a.k.a. black-box simulators). The likelihood of such models is typically intractable, which is why classical MCMC methods can not be used. Simulation-based inference (SBI) stands out in this context by only requiring a dataset of simulations to train deep generative models capable of approximating the posterior distribution that relates input parameters to a given observation. In this work, we consider a tall data extension in which multiple observations are available and one wishes to leverage their shared information to better infer the parameters of the model. The method we propose is built upon recent developments from the flourishing score-based diffusion literature and allows us to estimate the tall data posterior distribution simply using information from the score network trained on individual observations. We compare our method to recently proposed competing approaches on various numerical experiments and demonstrate its superiority in terms of numerical stability and computational cost.

Fast, accurate and lightweight sequential simulation-based inference using Gaussian locally linear mappings

Bayesian inference for complex models with an intractable likelihood can be tackled using algorithms performing many calls to computer simulators. These approaches are collectively known as "simulation-based inference" (SBI). Recent SBI methods have made use of neural networks (NN) to provide approximate, yet expressive constructs for the unavailable likelihood function and the posterior distribution. However, they do not generally achieve an optimal trade-off between accuracy and computational demand. In this work, we propose an alternative that provides both approximations to the likelihood and the posterior distribution, using structured mixtures of probability distributions. Our approach produces accurate posterior inference when compared to state-of-the-art NN-based SBI methods, while exhibiting a much smaller computational footprint. We illustrate our results on several benchmark models from the SBI literature.

L-C2ST: Local Diagnostics for Posterior Approximations in Simulation-Based Inference

Many recent works in simulation-based inference (SBI) rely on deep generative models to approximate complex, high-dimensional posterior distributions. However, evaluating whether or not these approximations can be trusted remains a challenge. Most approaches evaluate the posterior estimator only in expectation over the observation space. This limits their interpretability and is not sufficient to identify for which observations the approximation can be trusted or should be improved. Building upon the well-known classifier two-sample test (C2ST), we introduce L-C2ST, a new method that allows for a local evaluation of the posterior estimator at any given observation. It offers theoretically grounded and easy to interpret - e.g. graphical - diagnostics, and unlike C2ST, does not require access to samples from the true posterior. In the case of normalizing flow-based posterior estimators, L-C2ST can be specialized to offer better statistical power, while being computationally more efficient. On standard SBI benchmarks, L-C2ST provides comparable results to C2ST and outperforms alternative local approaches such as coverage tests based on highest predictive density (HPD). We further highlight the importance of local evaluation and the benefit of interpretability of L-C2ST on a challenging application from computational neuroscience.

Validation Diagnostics for SBI algorithms based on Normalizing Flows

Building on the recent trend of new deep generative models known as Normalizing Flows (NF), simulation-based inference (SBI) algorithms can now efficiently accommodate arbitrary complex and high-dimensional data distributions. The development of appropriate validation methods however has fallen behind. Indeed, most of the existing metrics either require access to the true posterior distribution, or fail to provide theoretical guarantees on the consistency of the inferred approximation beyond the one-dimensional setting. This work proposes easy to interpret validation diagnostics for multi-dimensional conditional (posterior) density estimators based on NF. It also offers theoretical guarantees based on results of local consistency. The proposed workflow can be used to check, analyse and guarantee consistent behavior of the estimator. The method is illustrated with a challenging example that involves tightly coupled parameters in the context of computational neuroscience. This work should help the design of better specified models or drive the development of novel SBI-algorithms, hence allowing to build up trust on their ability to address important questions in experimental science.

Leveraging Global Parameters for Flow-based Neural Posterior Estimation

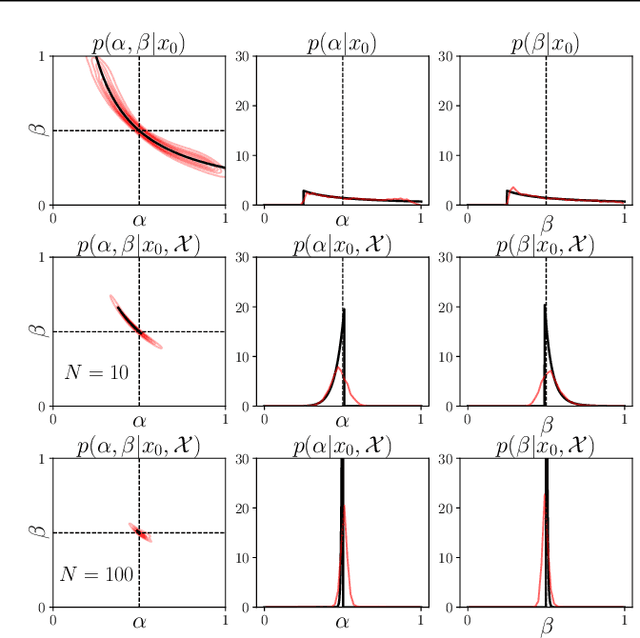
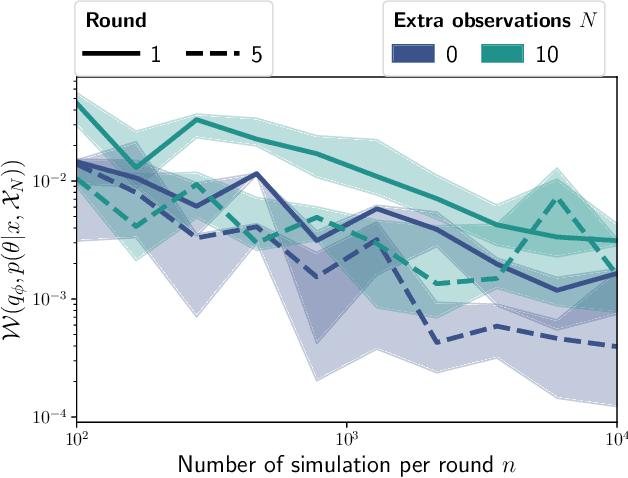
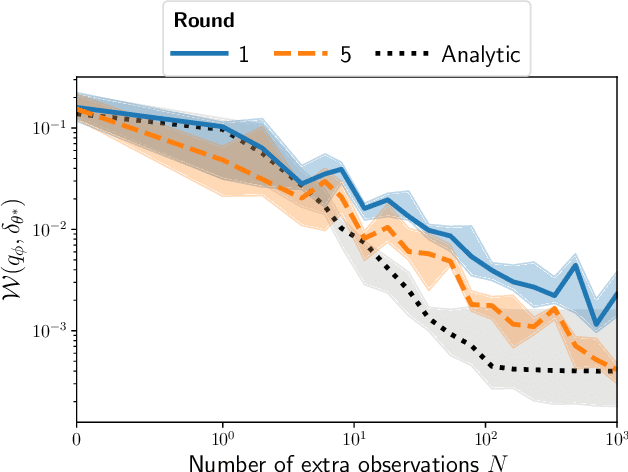
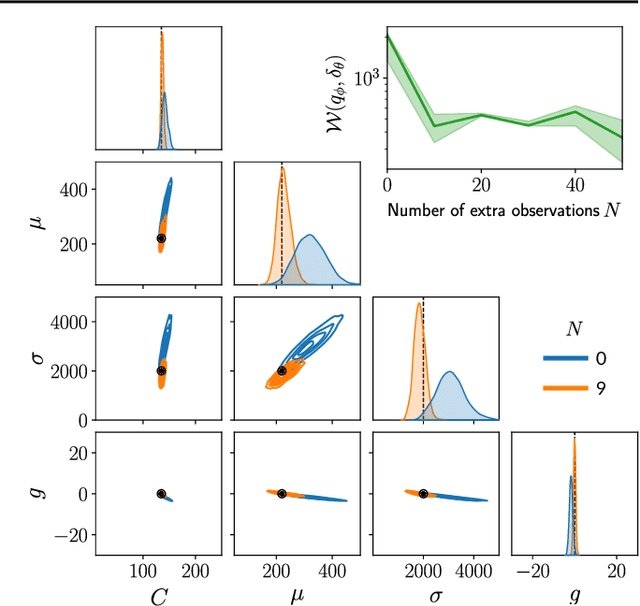
Inferring the parameters of a stochastic model based on experimental observations is central to the scientific method. A particularly challenging setting is when the model is strongly indeterminate, i.e., when distinct sets of parameters yield identical observations. This arises in many practical situations, such as when inferring the distance and power of a radio source (is the source close and weak or far and strong?) or when estimating the amplifier gain and underlying brain activity of an electrophysiological experiment. In this work, we present a method for cracking such indeterminacy by exploiting additional information conveyed by an auxiliary set of observations sharing global parameters. Our method extends recent developments in simulation-based inference(SBI) based on normalizing flows to Bayesian hierarchical models. We validate quantitatively our proposal on a motivating example amenable to analytical solutions, and then apply it to invert a well known non-linear model from computational neuroscience.