Predict-Project-Renoise: Sampling Diffusion Models under Hard Constraints

Neural emulators based on diffusion models show promise for scientific applications, but vanilla models cannot guarantee physical accuracy or constraint satisfaction. We address this by introducing a constrained sampling framework that enforces hard constraints, such as physical laws or observational consistency, at generation time. Our approach defines a constrained forward process that diffuses only over the feasible set of constraint-satisfying samples, inducing constrained marginal distributions. To reverse this, we propose Predict-Project-Renoise (PPR), an iterative algorithm that samples from the constrained marginals by alternating between denoising predictions, projecting onto the feasible set, and renoising. Experiments on 2D distributions, PDEs, and global weather forecasting demonstrate that PPR reduces constraint violations by over an order of magnitude while improving sample consistency and better matching the true constrained distribution compared to baselines.

Improving Semantic Uncertainty Quantification in LVLMs with Semantic Gaussian Processes

Large Vision-Language Models (LVLMs) often produce plausible but unreliable outputs, making robust uncertainty estimation essential. Recent work on semantic uncertainty estimates relies on external models to cluster multiple sampled responses and measure their semantic consistency. However, these clustering methods are often fragile, highly sensitive to minor phrasing variations, and can incorrectly group or separate semantically similar answers, leading to unreliable uncertainty estimates. We propose Semantic Gaussian Process Uncertainty (SGPU), a Bayesian framework that quantifies semantic uncertainty by analyzing the geometric structure of answer embeddings, avoiding brittle clustering. SGPU maps generated answers into a dense semantic space, computes the Gram matrix of their embeddings, and summarizes their semantic configuration via the eigenspectrum. This spectral representation is then fed into a Gaussian Process Classifier that learns to map patterns of semantic consistency to predictive uncertainty, and that can be applied in both black-box and white-box settings. Across six LLMs and LVLMs on eight datasets spanning VQA, image classification, and textual QA, SGPU consistently achieves state-of-the-art calibration (ECE) and discriminative (AUROC, AUARC) performance. We further show that SGPU transfers across models and modalities, indicating that its spectral representation captures general patterns of semantic uncertainty.

Lost in Latent Space: An Empirical Study of Latent Diffusion Models for Physics Emulation

The steep computational cost of diffusion models at inference hinders their use as fast physics emulators. In the context of image and video generation, this computational drawback has been addressed by generating in the latent space of an autoencoder instead of the pixel space. In this work, we investigate whether a similar strategy can be effectively applied to the emulation of dynamical systems and at what cost. We find that the accuracy of latent-space emulation is surprisingly robust to a wide range of compression rates (up to 1000x). We also show that diffusion-based emulators are consistently more accurate than non-generative counterparts and compensate for uncertainty in their predictions with greater diversity. Finally, we cover practical design choices, spanning from architectures to optimizers, that we found critical to train latent-space emulators.

Appa: Bending Weather Dynamics with Latent Diffusion Models for Global Data Assimilation

Deep learning has transformed weather forecasting by improving both its accuracy and computational efficiency. However, before any forecast can begin, weather centers must identify the current atmospheric state from vast amounts of observational data. To address this challenging problem, we introduce Appa, a score-based data assimilation model producing global atmospheric trajectories at 0.25-degree resolution and 1-hour intervals. Powered by a 1.5B-parameter spatio-temporal latent diffusion model trained on ERA5 reanalysis data, Appa can be conditioned on any type of observations to infer the posterior distribution of plausible state trajectories, without retraining. Our unified probabilistic framework flexibly tackles multiple inference tasks -- reanalysis, filtering, and forecasting -- using the same model, eliminating the need for task-specific architectures or training procedures. Experiments demonstrate physical consistency on a global scale and good reconstructions from observations, while showing competitive forecasting skills. Our results establish latent score-based data assimilation as a promising foundation for future global atmospheric modeling systems.

Costs Estimation in Unit Commitment Problems using Simulation-Based Inference

The Unit Commitment (UC) problem is a key optimization task in power systems to forecast the generation schedules of power units over a finite time period by minimizing costs while meeting demand and technical constraints. However, many parameters required by the UC problem are unknown, such as the costs. In this work, we estimate these unknown costs using simulation-based inference on an illustrative UC problem, which provides an approximated posterior distribution of the parameters given observed generation schedules and demands. Our results highlight that the learned posterior distribution effectively captures the underlying distribution of the data, providing a range of possible values for the unknown parameters given a past observation. This posterior allows for the estimation of past costs using observed past generation schedules, enabling operators to better forecast future costs and make more robust generation scheduling forecasts. We present avenues for future research to address overconfidence in posterior estimation, enhance the scalability of the methodology and apply it to more complex UC problems modeling the network constraints and renewable energy sources.

A Neural Material Point Method for Particle-based Simulations

Mesh-free Lagrangian methods are widely used for simulating fluids, solids, and their complex interactions due to their ability to handle large deformations and topological changes. These physics simulators, however, require substantial computational resources for accurate simulations. To address these issues, deep learning emulators promise faster and scalable simulations, yet they often remain expensive and difficult to train, limiting their practical use. Inspired by the Material Point Method (MPM), we present NeuralMPM, a neural emulation framework for particle-based simulations. NeuralMPM interpolates Lagrangian particles onto a fixed-size grid, computes updates on grid nodes using image-to-image neural networks, and interpolates back to the particles. Similarly to MPM, NeuralMPM benefits from the regular voxelized representation to simplify the computation of the state dynamics, while avoiding the drawbacks of mesh-based Eulerian methods. We demonstrate the advantages of NeuralMPM on several datasets, including fluid dynamics and fluid-solid interactions. Compared to existing methods, NeuralMPM reduces training times from days to hours, while achieving comparable or superior long-term accuracy, making it a promising approach for practical forward and inverse problems. A project page is available at https://neuralmpm.isach.be

Low-Budget Simulation-Based Inference with Bayesian Neural Networks

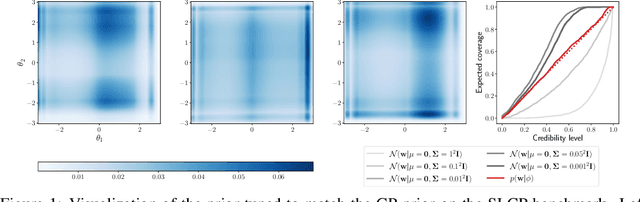
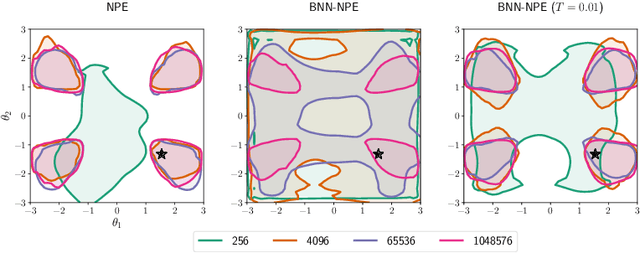
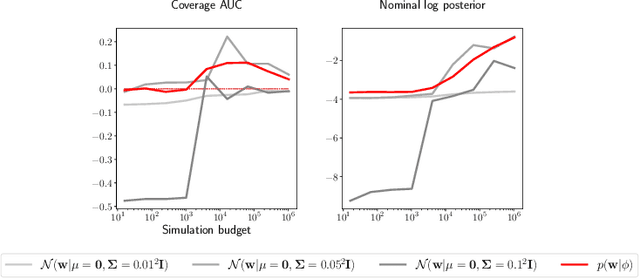
Simulation-based inference methods have been shown to be inaccurate in the data-poor regime, when training simulations are limited or expensive. Under these circumstances, the inference network is particularly prone to overfitting, and using it without accounting for the computational uncertainty arising from the lack of identifiability of the network weights can lead to unreliable results. To address this issue, we propose using Bayesian neural networks in low-budget simulation-based inference, thereby explicitly accounting for the computational uncertainty of the posterior approximation. We design a family of Bayesian neural network priors that are tailored for inference and show that they lead to well-calibrated posteriors on tested benchmarks, even when as few as $O(10)$ simulations are available. This opens up the possibility of performing reliable simulation-based inference using very expensive simulators, as we demonstrate on a problem from the field of cosmology where single simulations are computationally expensive. We show that Bayesian neural networks produce informative and well-calibrated posterior estimates with only a few hundred simulations.

Learning Diffusion Priors from Observations by Expectation Maximization

Diffusion models recently proved to be remarkable priors for Bayesian inverse problems. However, training these models typically requires access to large amounts of clean data, which could prove difficult in some settings. In this work, we present a novel method based on the expectation-maximization algorithm for training diffusion models from incomplete and noisy observations only. Unlike previous works, our method leads to proper diffusion models, which is crucial for downstream tasks. As part of our method, we propose and motivate a new posterior sampling scheme for unconditional diffusion models. We present empirical evidence supporting the effectiveness of our method.

Harnessing machine learning for accurate treatment of overlapping opacity species in GCMs

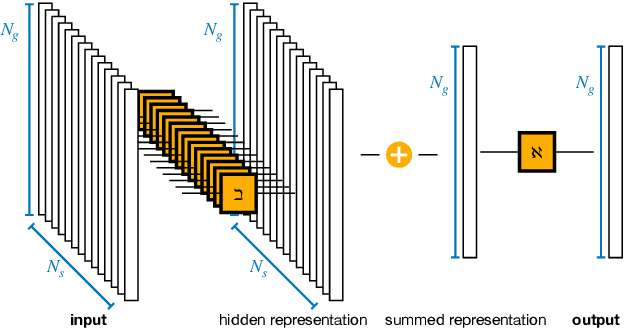
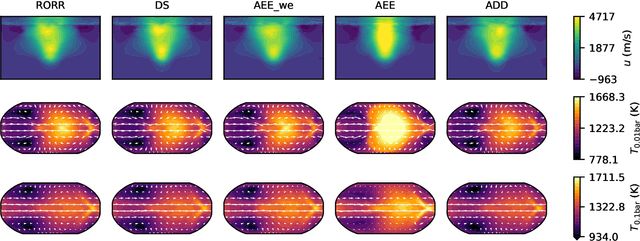
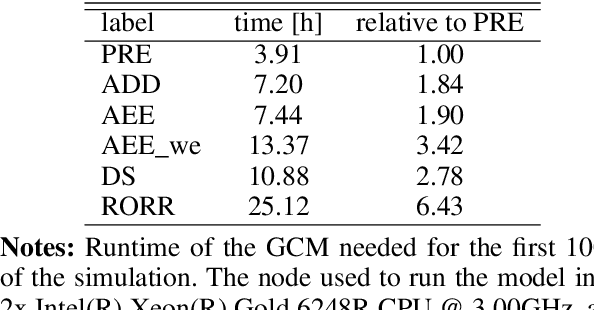
To understand high precision observations of exoplanets and brown dwarfs, we need detailed and complex general circulation models (GCMs) that incorporate hydrodynamics, chemistry, and radiation. In this study, we specifically examine the coupling between chemistry and radiation in GCMs and compare different methods for mixing opacities of different chemical species in the correlated-k assumption, when equilibrium chemistry cannot be assumed. We propose a fast machine learning method based on DeepSets (DS), which effectively combines individual correlated-k opacities (k-tables). We evaluate the DS method alongside other published methods like adaptive equivalent extinction (AEE) and random overlap with rebinning and resorting (RORR). We integrate these mixing methods into our GCM (expeRT/MITgcm) and assess their accuracy and performance for the example of the hot Jupiter HD~209458 b. Our findings indicate that the DS method is both accurate and efficient for GCM usage, whereas RORR is too slow. Additionally, we observe that the accuracy of AEE depends on its specific implementation and may introduce numerical issues in achieving radiative transfer solution convergence. We then apply the DS mixing method in a simplified chemical disequilibrium situation, where we model the rainout of TiO and VO, and confirm that the rainout of TiO and VO would hinder the formation of a stratosphere. To further expedite the development of consistent disequilibrium chemistry calculations in GCMs, we provide documentation and code for coupling the DS mixing method with correlated-k radiative transfer solvers. The DS method has been extensively tested to be accurate enough for GCMs, however, other methods might be needed for accelerating atmospheric retrievals.

Calibrating Neural Simulation-Based Inference with Differentiable Coverage Probability

Bayesian inference allows expressing the uncertainty of posterior belief under a probabilistic model given prior information and the likelihood of the evidence. Predominantly, the likelihood function is only implicitly established by a simulator posing the need for simulation-based inference (SBI). However, the existing algorithms can yield overconfident posteriors (Hermans *et al.*, 2022) defeating the whole purpose of credibility if the uncertainty quantification is inaccurate. We propose to include a calibration term directly into the training objective of the neural model in selected amortized SBI techniques. By introducing a relaxation of the classical formulation of calibration error we enable end-to-end backpropagation. The proposed method is not tied to any particular neural model and brings moderate computational overhead compared to the profits it introduces. It is directly applicable to existing computational pipelines allowing reliable black-box posterior inference. We empirically show on six benchmark problems that the proposed method achieves competitive or better results in terms of coverage and expected posterior density than the previously existing approaches.