The Well: a Large-Scale Collection of Diverse Physics Simulations for Machine Learning

Machine learning based surrogate models offer researchers powerful tools for accelerating simulation-based workflows. However, as standard datasets in this space often cover small classes of physical behavior, it can be difficult to evaluate the efficacy of new approaches. To address this gap, we introduce the Well: a large-scale collection of datasets containing numerical simulations of a wide variety of spatiotemporal physical systems. The Well draws from domain experts and numerical software developers to provide 15TB of data across 16 datasets covering diverse domains such as biological systems, fluid dynamics, acoustic scattering, as well as magneto-hydrodynamic simulations of extra-galactic fluids or supernova explosions. These datasets can be used individually or as part of a broader benchmark suite. To facilitate usage of the Well, we provide a unified PyTorch interface for training and evaluating models. We demonstrate the function of this library by introducing example baselines that highlight the new challenges posed by the complex dynamics of the Well. The code and data is available at https://github.com/PolymathicAI/the_well.

Learning Diffusion Priors from Observations by Expectation Maximization

Diffusion models recently proved to be remarkable priors for Bayesian inverse problems. However, training these models typically requires access to large amounts of clean data, which could prove difficult in some settings. In this work, we present a novel method based on the expectation-maximization algorithm for training diffusion models from incomplete and noisy observations only. Unlike previous works, our method leads to proper diffusion models, which is crucial for downstream tasks. As part of our method, we propose and motivate a new posterior sampling scheme for unconditional diffusion models. We present empirical evidence supporting the effectiveness of our method.

Score-based Data Assimilation for a Two-Layer Quasi-Geostrophic Model

Data assimilation addresses the problem of identifying plausible state trajectories of dynamical systems given noisy or incomplete observations. In geosciences, it presents challenges due to the high-dimensionality of geophysical dynamical systems, often exceeding millions of dimensions. This work assesses the scalability of score-based data assimilation (SDA), a novel data assimilation method, in the context of such systems. We propose modifications to the score network architecture aimed at significantly reducing memory consumption and execution time. We demonstrate promising results for a two-layer quasi-geostrophic model.

Score-based Data Assimilation

Data assimilation, in its most comprehensive form, addresses the Bayesian inverse problem of identifying plausible state trajectories that explain noisy or incomplete observations of stochastic dynamical systems. Various approaches have been proposed to solve this problem, including particle-based and variational methods. However, most algorithms depend on the transition dynamics for inference, which becomes intractable for long time horizons or for high-dimensional systems with complex dynamics, such as oceans or atmospheres. In this work, we introduce score-based data assimilation for trajectory inference. We learn a score-based generative model of state trajectories based on the key insight that the score of an arbitrarily long trajectory can be decomposed into a series of scores over short segments. After training, inference is carried out using the score model, in a non-autoregressive manner by generating all states simultaneously. Quite distinctively, we decouple the observation model from the training procedure and use it only at inference to guide the generative process, which enables a wide range of zero-shot observation scenarios. We present theoretical and empirical evidence supporting the effectiveness of our method.

Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation

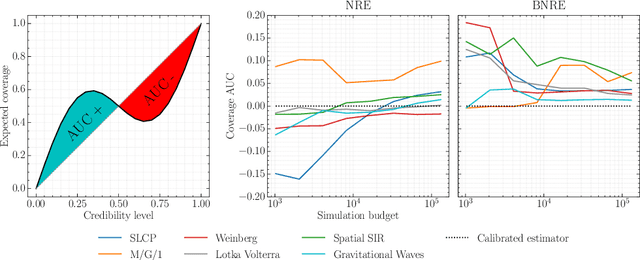
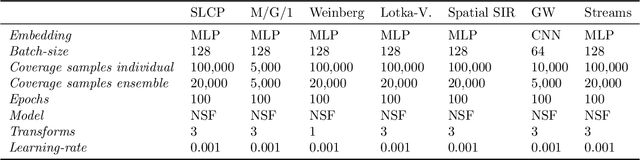
Modern approaches for simulation-based inference rely upon deep learning surrogates to enable approximate inference with computer simulators. In practice, the estimated posteriors' computational faithfulness is, however, rarely guaranteed. For example, Hermans et al. (2021) show that current simulation-based inference algorithms can produce posteriors that are overconfident, hence risking false inferences. In this work, we introduce Balanced Neural Ratio Estimation (BNRE), a variation of the NRE algorithm designed to produce posterior approximations that tend to be more conservative, hence improving their reliability, while sharing the same Bayes optimal solution. We achieve this by enforcing a balancing condition that increases the quantified uncertainty in small simulation budget regimes while still converging to the exact posterior as the budget increases. We provide theoretical arguments showing that BNRE tends to produce posterior surrogates that are more conservative than NRE's. We evaluate BNRE on a wide variety of tasks and show that it produces conservative posterior surrogates on all tested benchmarks and simulation budgets. Finally, we emphasize that BNRE is straightforward to implement over NRE and does not introduce any computational overhead.

Averting A Crisis In Simulation-Based Inference

We present extensive empirical evidence showing that current Bayesian simulation-based inference algorithms are inadequate for the falsificationist methodology of scientific inquiry. Our results collected through months of experimental computations show that all benchmarked algorithms -- (S)NPE, (S)NRE, SNL and variants of ABC -- may produce overconfident posterior approximations, which makes them demonstrably unreliable and dangerous if one's scientific goal is to constrain parameters of interest. We believe that failing to address this issue will lead to a well-founded trust crisis in simulation-based inference. For this reason, we argue that research efforts should now consider theoretical and methodological developments of conservative approximate inference algorithms and present research directions towards this objective. In this regard, we show empirical evidence that ensembles are consistently more reliable.

Arbitrary Marginal Neural Ratio Estimation for Simulation-based Inference

In many areas of science, complex phenomena are modeled by stochastic parametric simulators, often featuring high-dimensional parameter spaces and intractable likelihoods. In this context, performing Bayesian inference can be challenging. In this work, we present a novel method that enables amortized inference over arbitrary subsets of the parameters, without resorting to numerical integration, which makes interpretation of the posterior more convenient. Our method is efficient and can be implemented with arbitrary neural network architectures. We demonstrate the applicability of the method on parameter inference of binary black hole systems from gravitational waves observations.