Joeri Hermans
Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation
Aug 29, 2022

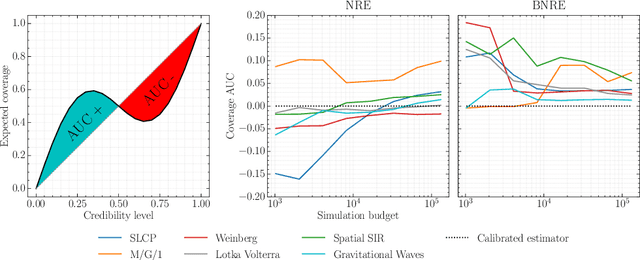

Abstract:Modern approaches for simulation-based inference rely upon deep learning surrogates to enable approximate inference with computer simulators. In practice, the estimated posteriors' computational faithfulness is, however, rarely guaranteed. For example, Hermans et al. (2021) show that current simulation-based inference algorithms can produce posteriors that are overconfident, hence risking false inferences. In this work, we introduce Balanced Neural Ratio Estimation (BNRE), a variation of the NRE algorithm designed to produce posterior approximations that tend to be more conservative, hence improving their reliability, while sharing the same Bayes optimal solution. We achieve this by enforcing a balancing condition that increases the quantified uncertainty in small simulation budget regimes while still converging to the exact posterior as the budget increases. We provide theoretical arguments showing that BNRE tends to produce posterior surrogates that are more conservative than NRE's. We evaluate BNRE on a wide variety of tasks and show that it produces conservative posterior surrogates on all tested benchmarks and simulation budgets. Finally, we emphasize that BNRE is straightforward to implement over NRE and does not introduce any computational overhead.
Averting A Crisis In Simulation-Based Inference
Oct 14, 2021


Abstract:We present extensive empirical evidence showing that current Bayesian simulation-based inference algorithms are inadequate for the falsificationist methodology of scientific inquiry. Our results collected through months of experimental computations show that all benchmarked algorithms -- (S)NPE, (S)NRE, SNL and variants of ABC -- may produce overconfident posterior approximations, which makes them demonstrably unreliable and dangerous if one's scientific goal is to constrain parameters of interest. We believe that failing to address this issue will lead to a well-founded trust crisis in simulation-based inference. For this reason, we argue that research efforts should now consider theoretical and methodological developments of conservative approximate inference algorithms and present research directions towards this objective. In this regard, we show empirical evidence that ensembles are consistently more reliable.
Towards constraining warm dark matter with stellar streams through neural simulation-based inference
Nov 30, 2020



Abstract:A statistical analysis of the observed perturbations in the density of stellar streams can in principle set stringent contraints on the mass function of dark matter subhaloes, which in turn can be used to constrain the mass of the dark matter particle. However, the likelihood of a stellar density with respect to the stream and subhaloes parameters involves solving an intractable inverse problem which rests on the integration of all possible forward realisations implicitly defined by the simulation model. In order to infer the subhalo abundance, previous analyses have relied on Approximate Bayesian Computation (ABC) together with domain-motivated but handcrafted summary statistics. Here, we introduce a likelihood-free Bayesian inference pipeline based on Amortised Approximate Likelihood Ratios (AALR), which automatically learns a mapping between the data and the simulator parameters and obviates the need to handcraft a possibly insufficient summary statistic. We apply the method to the simplified case where stellar streams are only perturbed by dark matter subhaloes, thus neglecting baryonic substructures, and describe several diagnostics that demonstrate the effectiveness of the new method and the statistical quality of the learned estimator.
Mining for Dark Matter Substructure: Inferring subhalo population properties from strong lenses with machine learning
Oct 17, 2019



Abstract:The subtle and unique imprint of dark matter substructure on extended arcs in strong lensing systems contains a wealth of information about the properties and distribution of dark matter on small scales and, consequently, about the underlying particle physics. However, teasing out this effect poses a significant challenge since the likelihood function for realistic simulations of population-level parameters is intractable. We apply recently-developed simulation-based inference techniques to the problem of substructure inference in galaxy-galaxy strong lenses. By leveraging additional information extracted from the simulator, neural networks are efficiently trained to estimate likelihood ratios associated with population-level parameters characterizing substructure. Through proof-of-principle application to simulated data, we show that these methods can provide an efficient and principled way to simultaneously analyze an ensemble of strong lenses, and can be used to mine the large sample of lensing images deliverable by near-future surveys for signatures of dark matter substructure.
Likelihood-free MCMC with Approximate Likelihood Ratios
Mar 10, 2019



Abstract:We propose a novel approach for posterior sampling with intractable likelihoods. This is an increasingly important problem in scientific applications where models are implemented as sophisticated computer simulations. As a result, tractable densities are not available, which forces practitioners to rely on approximations during inference. We address the intractability of densities by training a parameterized classifier whose output is used to approximate likelihood ratios between arbitrary model parameters. In turn, we are able to draw posterior samples by plugging this approximator into common Markov chain Monte Carlo samplers such as Metropolis-Hastings and Hamiltonian Monte Carlo. We demonstrate the proposed technique by fitting the generating parameters of implicit models, ranging from a linear probabilistic model to settings in high energy physics with high-dimensional observations. Finally, we discuss several diagnostics to assess the quality of the posterior.
Adversarial Variational Optimization of Non-Differentiable Simulators
Oct 05, 2018



Abstract:Complex computer simulators are increasingly used across fields of science as generative models tying parameters of an underlying theory to experimental observations. Inference in this setup is often difficult, as simulators rarely admit a tractable density or likelihood function. We introduce Adversarial Variational Optimization (AVO), a likelihood-free inference algorithm for fitting a non-differentiable generative model incorporating ideas from generative adversarial networks, variational optimization and empirical Bayes. We adapt the training procedure of generative adversarial networks by replacing the differentiable generative network with a domain-specific simulator. We solve the resulting non-differentiable minimax problem by minimizing variational upper bounds of the two adversarial objectives. Effectively, the procedure results in learning a proposal distribution over simulator parameters, such that the JS divergence between the marginal distribution of the synthetic data and the empirical distribution of observed data is minimized. We evaluate and compare the method with simulators producing both discrete and continuous data.
Gradient Energy Matching for Distributed Asynchronous Gradient Descent
May 22, 2018



Abstract:Distributed asynchronous SGD has become widely used for deep learning in large-scale systems, but remains notorious for its instability when increasing the number of workers. In this work, we study the dynamics of distributed asynchronous SGD under the lens of Lagrangian mechanics. Using this description, we introduce the concept of energy to describe the optimization process and derive a sufficient condition ensuring its stability as long as the collective energy induced by the active workers remains below the energy of a target synchronous process. Making use of this criterion, we derive a stable distributed asynchronous optimization procedure, GEM, that estimates and maintains the energy of the asynchronous system below or equal to the energy of sequential SGD with momentum. Experimental results highlight the stability and speedup of GEM compared to existing schemes, even when scaling to one hundred asynchronous workers. Results also indicate better generalization compared to the targeted SGD with momentum.
Accumulated Gradient Normalization
Oct 06, 2017



Abstract:This work addresses the instability in asynchronous data parallel optimization. It does so by introducing a novel distributed optimizer which is able to efficiently optimize a centralized model under communication constraints. The optimizer achieves this by pushing a normalized sequence of first-order gradients to a parameter server. This implies that the magnitude of a worker delta is smaller compared to an accumulated gradient, and provides a better direction towards a minimum compared to first-order gradients, which in turn also forces possible implicit momentum fluctuations to be more aligned since we make the assumption that all workers contribute towards a single minima. As a result, our approach mitigates the parameter staleness problem more effectively since staleness in asynchrony induces (implicit) momentum, and achieves a better convergence rate compared to other optimizers such as asynchronous EASGD and DynSGD, which we show empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge