Leveraging Cardiovascular Simulations for In-Vivo Prediction of Cardiac Biomarkers

Whole-body hemodynamics simulators, which model blood flow and pressure waveforms as functions of physiological parameters, are now essential tools for studying cardiovascular systems. However, solving the corresponding inverse problem of mapping observations (e.g., arterial pressure waveforms at specific locations in the arterial network) back to plausible physiological parameters remains challenging. Leveraging recent advances in simulation-based inference, we cast this problem as statistical inference by training an amortized neural posterior estimator on a newly built large dataset of cardiac simulations that we publicly release. To better align simulated data with real-world measurements, we incorporate stochastic elements modeling exogenous effects. The proposed framework can further integrate in-vivo data sources to refine its predictive capabilities on real-world data. In silico, we demonstrate that the proposed framework enables finely quantifying uncertainty associated with individual measurements, allowing trustworthy prediction of four biomarkers of clinical interest--namely Heart Rate, Cardiac Output, Systemic Vascular Resistance, and Left Ventricular Ejection Time--from arterial pressure waveforms and photoplethysmograms. Furthermore, we validate the framework in vivo, where our method accurately captures temporal trends in CO and SVR monitoring on the VitalDB dataset. Finally, the predictive error made by the model monotonically increases with the predicted uncertainty, thereby directly supporting the automatic rejection of unusable measurements.

Addressing Misspecification in Simulation-based Inference through Data-driven Calibration

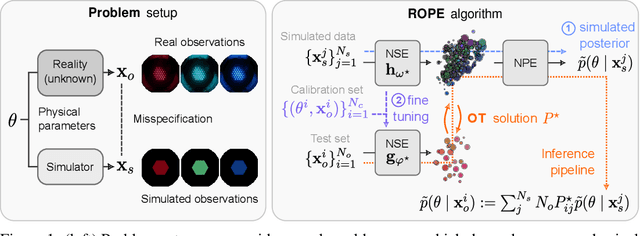
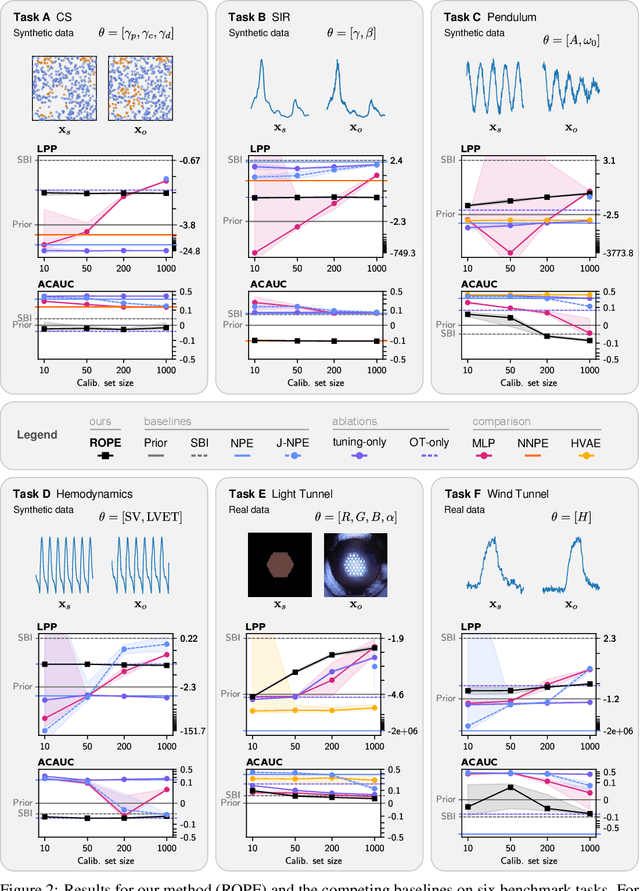
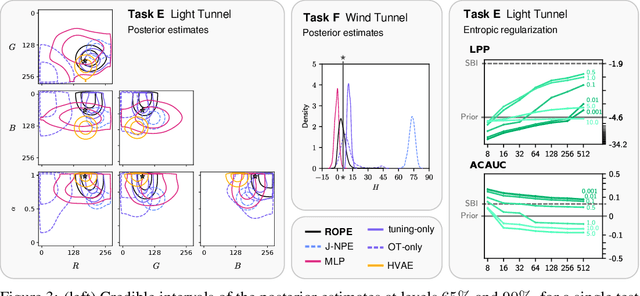
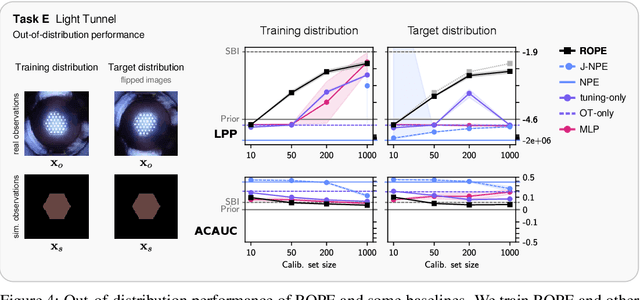
Driven by steady progress in generative modeling, simulation-based inference (SBI) has enabled inference over stochastic simulators. However, recent work has demonstrated that model misspecification can harm SBI's reliability. This work introduces robust posterior estimation (ROPE), a framework that overcomes model misspecification with a small real-world calibration set of ground truth parameter measurements. We formalize the misspecification gap as the solution of an optimal transport problem between learned representations of real-world and simulated observations. Assuming the prior distribution over the parameters of interest is known and well-specified, our method offers a controllable balance between calibrated uncertainty and informative inference under all possible misspecifications of the simulator. Our empirical results on four synthetic tasks and two real-world problems demonstrate that ROPE outperforms baselines and consistently returns informative and calibrated credible intervals.

Calibrating Neural Simulation-Based Inference with Differentiable Coverage Probability

Bayesian inference allows expressing the uncertainty of posterior belief under a probabilistic model given prior information and the likelihood of the evidence. Predominantly, the likelihood function is only implicitly established by a simulator posing the need for simulation-based inference (SBI). However, the existing algorithms can yield overconfident posteriors (Hermans *et al.*, 2022) defeating the whole purpose of credibility if the uncertainty quantification is inaccurate. We propose to include a calibration term directly into the training objective of the neural model in selected amortized SBI techniques. By introducing a relaxation of the classical formulation of calibration error we enable end-to-end backpropagation. The proposed method is not tied to any particular neural model and brings moderate computational overhead compared to the profits it introduces. It is directly applicable to existing computational pipelines allowing reliable black-box posterior inference. We empirically show on six benchmark problems that the proposed method achieves competitive or better results in terms of coverage and expected posterior density than the previously existing approaches.

Simulation-based Inference for Cardiovascular Models

Over the past decades, hemodynamics simulators have steadily evolved and have become tools of choice for studying cardiovascular systems in-silico. While such tools are routinely used to simulate whole-body hemodynamics from physiological parameters, solving the corresponding inverse problem of mapping waveforms back to plausible physiological parameters remains both promising and challenging. Motivated by advances in simulation-based inference (SBI), we cast this inverse problem as statistical inference. In contrast to alternative approaches, SBI provides \textit{posterior distributions} for the parameters of interest, providing a \textit{multi-dimensional} representation of uncertainty for \textit{individual} measurements. We showcase this ability by performing an in-silico uncertainty analysis of five biomarkers of clinical interest comparing several measurement modalities. Beyond the corroboration of known facts, such as the feasibility of estimating heart rate, our study highlights the potential of estimating new biomarkers from standard-of-care measurements. SBI reveals practically relevant findings that cannot be captured by standard sensitivity analyses, such as the existence of sub-populations for which parameter estimation exhibits distinct uncertainty regimes. Finally, we study the gap between in-vivo and in-silico with the MIMIC-III waveform database and critically discuss how cardiovascular simulations can inform real-world data analysis.

Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation

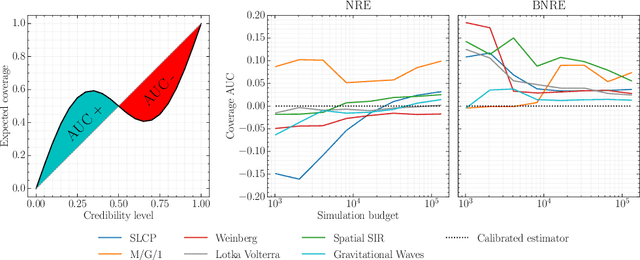
Modern approaches for simulation-based inference rely upon deep learning surrogates to enable approximate inference with computer simulators. In practice, the estimated posteriors' computational faithfulness is, however, rarely guaranteed. For example, Hermans et al. (2021) show that current simulation-based inference algorithms can produce posteriors that are overconfident, hence risking false inferences. In this work, we introduce Balanced Neural Ratio Estimation (BNRE), a variation of the NRE algorithm designed to produce posterior approximations that tend to be more conservative, hence improving their reliability, while sharing the same Bayes optimal solution. We achieve this by enforcing a balancing condition that increases the quantified uncertainty in small simulation budget regimes while still converging to the exact posterior as the budget increases. We provide theoretical arguments showing that BNRE tends to produce posterior surrogates that are more conservative than NRE's. We evaluate BNRE on a wide variety of tasks and show that it produces conservative posterior surrogates on all tested benchmarks and simulation budgets. Finally, we emphasize that BNRE is straightforward to implement over NRE and does not introduce any computational overhead.

Robust Hybrid Learning With Expert Augmentation

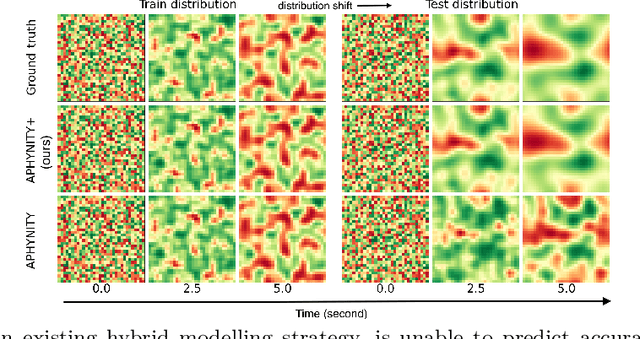
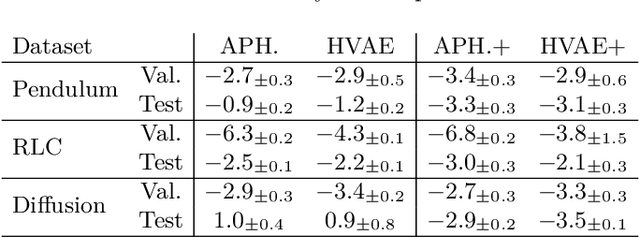
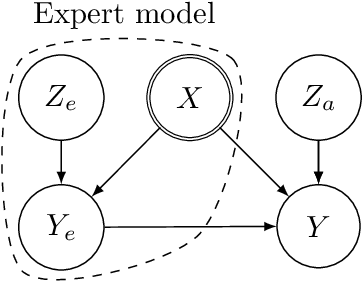
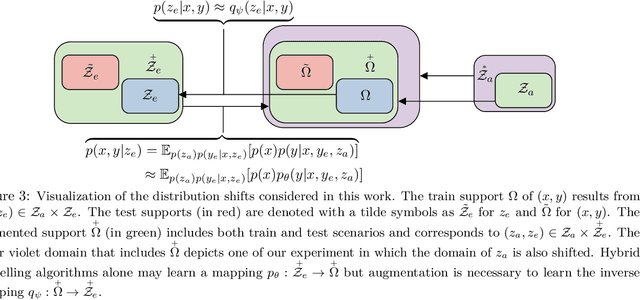
Hybrid modelling reduces the misspecification of expert models by combining them with machine learning (ML) components learned from data. Like for many ML algorithms, hybrid model performance guarantees are limited to the training distribution. Leveraging the insight that the expert model is usually valid even outside the training domain, we overcome this limitation by introducing a hybrid data augmentation strategy termed \textit{expert augmentation}. Based on a probabilistic formalization of hybrid modelling, we show why expert augmentation improves generalization. Finally, we validate the practical benefits of augmented hybrid models on a set of controlled experiments, modelling dynamical systems described by ordinary and partial differential equations.

Averting A Crisis In Simulation-Based Inference

We present extensive empirical evidence showing that current Bayesian simulation-based inference algorithms are inadequate for the falsificationist methodology of scientific inquiry. Our results collected through months of experimental computations show that all benchmarked algorithms -- (S)NPE, (S)NRE, SNL and variants of ABC -- may produce overconfident posterior approximations, which makes them demonstrably unreliable and dangerous if one's scientific goal is to constrain parameters of interest. We believe that failing to address this issue will lead to a well-founded trust crisis in simulation-based inference. For this reason, we argue that research efforts should now consider theoretical and methodological developments of conservative approximate inference algorithms and present research directions towards this objective. In this regard, we show empirical evidence that ensembles are consistently more reliable.

Diffusion Priors In Variational Autoencoders

Among likelihood-based approaches for deep generative modelling, variational autoencoders (VAEs) offer scalable amortized posterior inference and fast sampling. However, VAEs are also more and more outperformed by competing models such as normalizing flows (NFs), deep-energy models, or the new denoising diffusion probabilistic models (DDPMs). In this preliminary work, we improve VAEs by demonstrating how DDPMs can be used for modelling the prior distribution of the latent variables. The diffusion prior model improves upon Gaussian priors of classical VAEs and is competitive with NF-based priors. Finally, we hypothesize that hierarchical VAEs could similarly benefit from the enhanced capacity of diffusion priors.

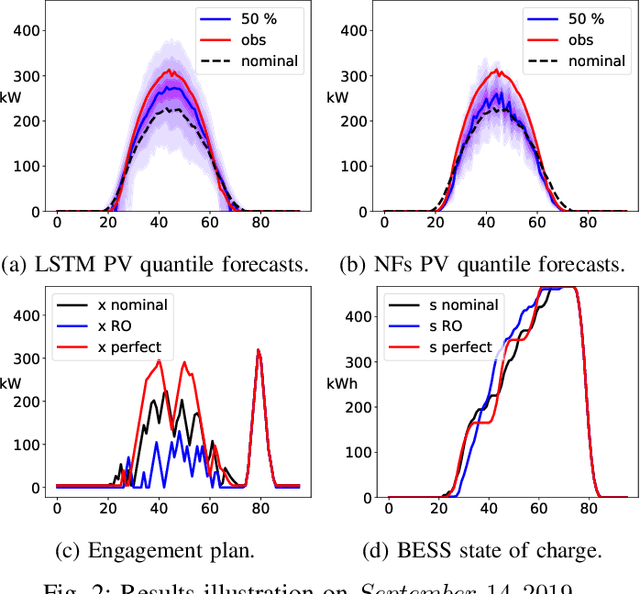
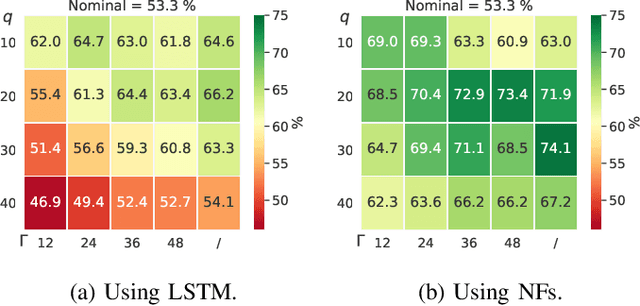
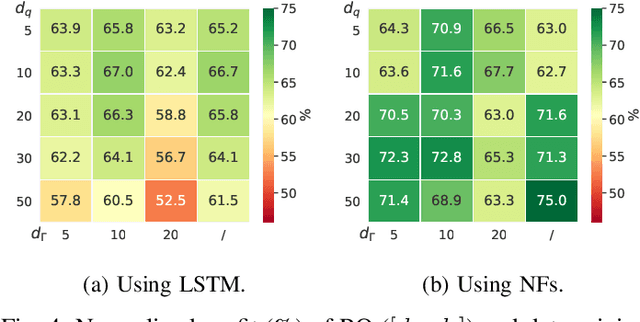
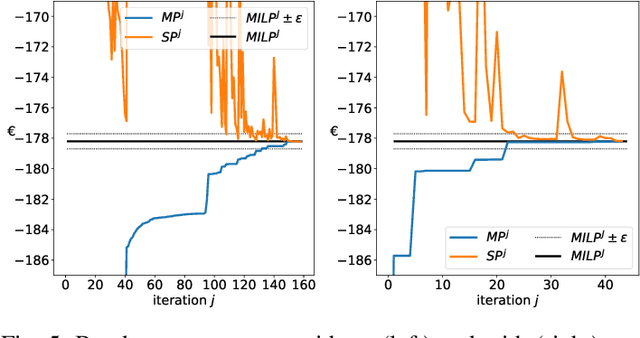
A Probabilistic Forecast-Driven Strategy for a Risk-Aware Participation in the Capacity Firming Market

The core contribution is to propose a probabilistic forecast-driven strategy, modeled as a min-max-min robust optimization problem with recourse, and solved using a Benders-dual cutting plane algorithm in a tractable manner. The convergence is improved by building an initial set of cuts. In addition, a dynamic risk-averse parameters selection strategy based on the quantile forecasts distribution is proposed. A secondary contribution is to use a recently developed deep learning model known as normalizing flows to generate quantile forecasts of renewable generation for the robust optimization problem. This technique provides a general mechanism for defining expressive probability distributions, only requiring the specification of a base distribution and a series of bijective transformations. Overall, the robust approach improves the results over a deterministic approach with nominal point forecasts by finding a trade-off between conservative and risk-seeking policies. The case study uses the photovoltaic generation monitored on-site at the University of Li\`ege (ULi\`ege), Belgium.

Distributional Reinforcement Learning with Unconstrained Monotonic Neural Networks

The distributional reinforcement learning (RL) approach advocates for representing the complete probability distribution of the random return instead of only modelling its expectation. A distributional RL algorithm may be characterised by two main components, namely the representation and parameterisation of the distribution and the probability metric defining the loss. This research considers the unconstrained monotonic neural network (UMNN) architecture, a universal approximator of continuous monotonic functions which is particularly well suited for modelling different representations of a distribution (PDF, CDF, quantile function). This property enables the decoupling of the effect of the function approximator class from that of the probability metric. The paper firstly introduces a methodology for learning different representations of the random return distribution. Secondly, a novel distributional RL algorithm named unconstrained monotonic deep Q-network (UMDQN) is presented. Lastly, in light of this new algorithm, an empirical comparison is performed between three probability quasimetrics, namely the Kullback-Leibler divergence, Cramer distance and Wasserstein distance. The results call for a reconsideration of all probability metrics in distributional RL, which contrasts with the dominance of the Wasserstein distance in recent publications.