Leveraging Cardiovascular Simulations for In-Vivo Prediction of Cardiac Biomarkers

Whole-body hemodynamics simulators, which model blood flow and pressure waveforms as functions of physiological parameters, are now essential tools for studying cardiovascular systems. However, solving the corresponding inverse problem of mapping observations (e.g., arterial pressure waveforms at specific locations in the arterial network) back to plausible physiological parameters remains challenging. Leveraging recent advances in simulation-based inference, we cast this problem as statistical inference by training an amortized neural posterior estimator on a newly built large dataset of cardiac simulations that we publicly release. To better align simulated data with real-world measurements, we incorporate stochastic elements modeling exogenous effects. The proposed framework can further integrate in-vivo data sources to refine its predictive capabilities on real-world data. In silico, we demonstrate that the proposed framework enables finely quantifying uncertainty associated with individual measurements, allowing trustworthy prediction of four biomarkers of clinical interest--namely Heart Rate, Cardiac Output, Systemic Vascular Resistance, and Left Ventricular Ejection Time--from arterial pressure waveforms and photoplethysmograms. Furthermore, we validate the framework in vivo, where our method accurately captures temporal trends in CO and SVR monitoring on the VitalDB dataset. Finally, the predictive error made by the model monotonically increases with the predicted uncertainty, thereby directly supporting the automatic rejection of unusable measurements.

Addressing Misspecification in Simulation-based Inference through Data-driven Calibration

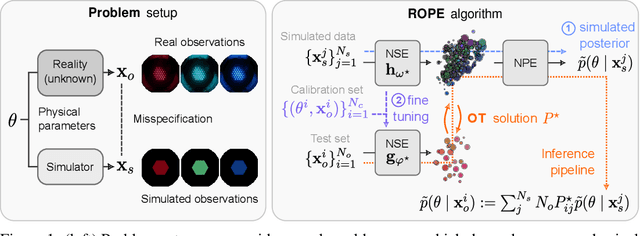
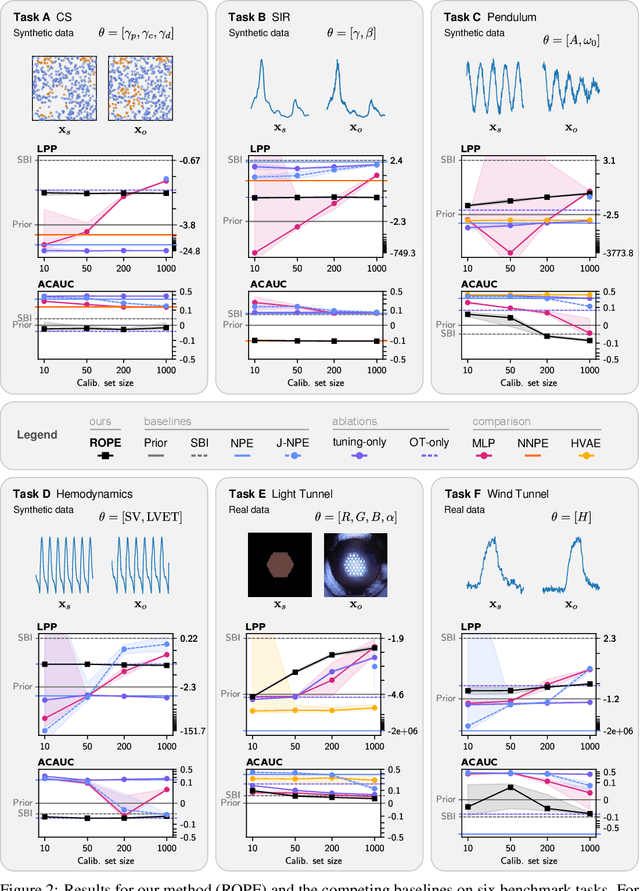
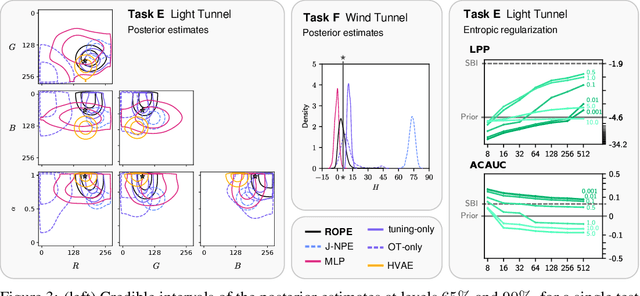
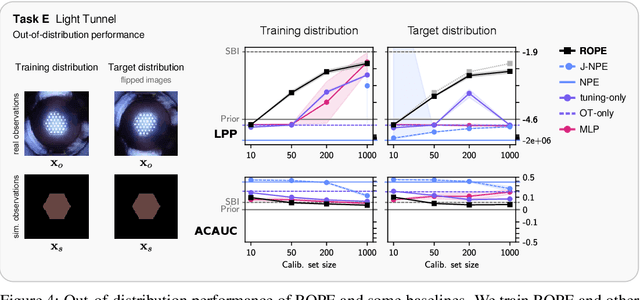
Driven by steady progress in generative modeling, simulation-based inference (SBI) has enabled inference over stochastic simulators. However, recent work has demonstrated that model misspecification can harm SBI's reliability. This work introduces robust posterior estimation (ROPE), a framework that overcomes model misspecification with a small real-world calibration set of ground truth parameter measurements. We formalize the misspecification gap as the solution of an optimal transport problem between learned representations of real-world and simulated observations. Assuming the prior distribution over the parameters of interest is known and well-specified, our method offers a controllable balance between calibrated uncertainty and informative inference under all possible misspecifications of the simulator. Our empirical results on four synthetic tasks and two real-world problems demonstrate that ROPE outperforms baselines and consistently returns informative and calibrated credible intervals.

Simulation-based Inference for Cardiovascular Models

Over the past decades, hemodynamics simulators have steadily evolved and have become tools of choice for studying cardiovascular systems in-silico. While such tools are routinely used to simulate whole-body hemodynamics from physiological parameters, solving the corresponding inverse problem of mapping waveforms back to plausible physiological parameters remains both promising and challenging. Motivated by advances in simulation-based inference (SBI), we cast this inverse problem as statistical inference. In contrast to alternative approaches, SBI provides \textit{posterior distributions} for the parameters of interest, providing a \textit{multi-dimensional} representation of uncertainty for \textit{individual} measurements. We showcase this ability by performing an in-silico uncertainty analysis of five biomarkers of clinical interest comparing several measurement modalities. Beyond the corroboration of known facts, such as the feasibility of estimating heart rate, our study highlights the potential of estimating new biomarkers from standard-of-care measurements. SBI reveals practically relevant findings that cannot be captured by standard sensitivity analyses, such as the existence of sub-populations for which parameter estimation exhibits distinct uncertainty regimes. Finally, we study the gap between in-vivo and in-silico with the MIMIC-III waveform database and critically discuss how cardiovascular simulations can inform real-world data analysis.

Robust Hybrid Learning With Expert Augmentation

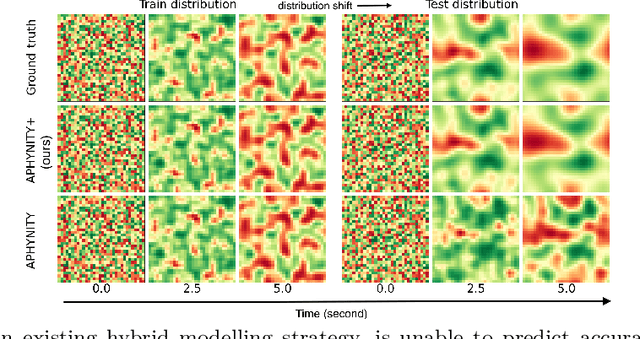
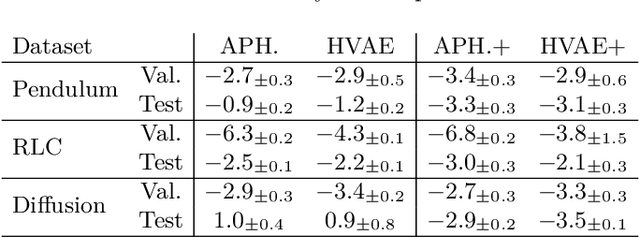
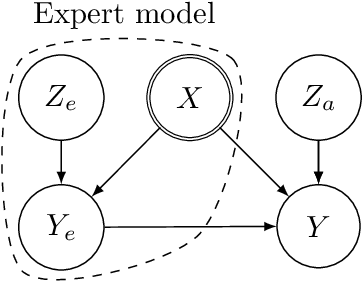
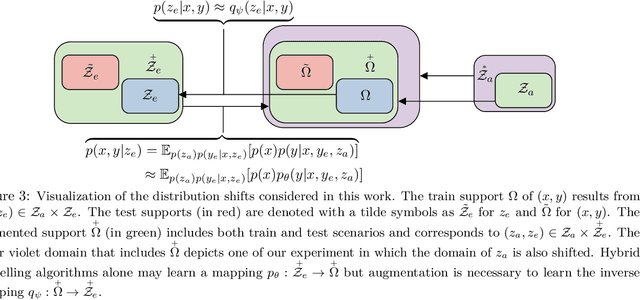
Hybrid modelling reduces the misspecification of expert models by combining them with machine learning (ML) components learned from data. Like for many ML algorithms, hybrid model performance guarantees are limited to the training distribution. Leveraging the insight that the expert model is usually valid even outside the training domain, we overcome this limitation by introducing a hybrid data augmentation strategy termed \textit{expert augmentation}. Based on a probabilistic formalization of hybrid modelling, we show why expert augmentation improves generalization. Finally, we validate the practical benefits of augmented hybrid models on a set of controlled experiments, modelling dynamical systems described by ordinary and partial differential equations.

Generalization of the Change of Variables Formula with Applications to Residual Flows

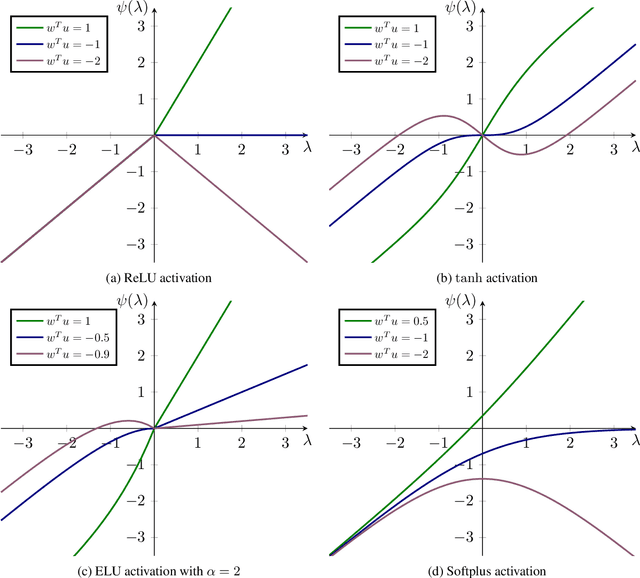
Normalizing flows leverage the Change of Variables Formula (CVF) to define flexible density models. Yet, the requirement of smooth transformations (diffeomorphisms) in the CVF poses a significant challenge in the construction of these models. To enlarge the design space of flows, we introduce $\mathcal{L}$-diffeomorphisms as generalized transformations which may violate these requirements on zero Lebesgue-measure sets. This relaxation allows e.g. the use of non-smooth activation functions such as ReLU. Finally, we apply the obtained results to planar, radial, and contractive residual flows.

Understanding and mitigating exploding inverses in invertible neural networks

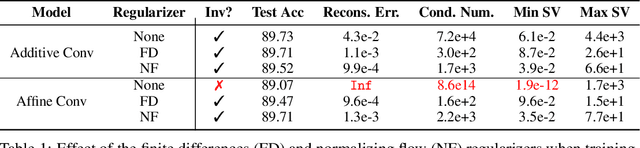
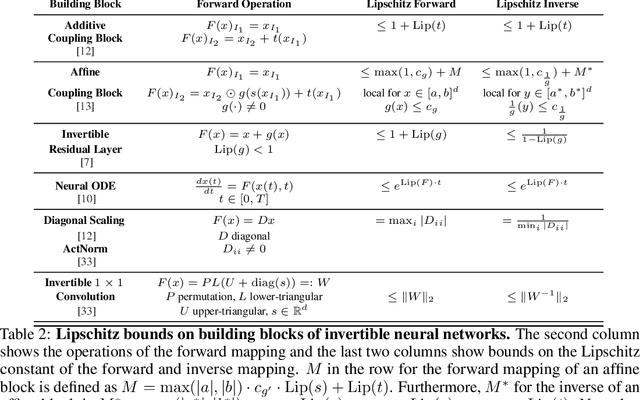
Invertible neural networks (INNs) have been used to design generative models, implement memory-saving gradient computation, and solve inverse problems. In this work, we show that commonly-used INN architectures suffer from exploding inverses and are thus prone to becoming numerically non-invertible. Across a wide range of INN use-cases, we reveal failures including the non-applicability of the change-of-variables formula on in- and out-of-distribution (OOD) data, incorrect gradients for memory-saving backprop, and the inability to sample from normalizing flow models. We further derive bi-Lipschitz properties of atomic building blocks of common architectures. These insights into the stability of INNs then provide ways forward to remedy these failures. For tasks where local invertibility is sufficient, like memory-saving backprop, we propose a flexible and efficient regularizer. For problems where global invertibility is necessary, such as applying normalizing flows on OOD data, we show the importance of designing stable INN building blocks.

Fundamental Tradeoffs between Invariance and Sensitivity to Adversarial Perturbations

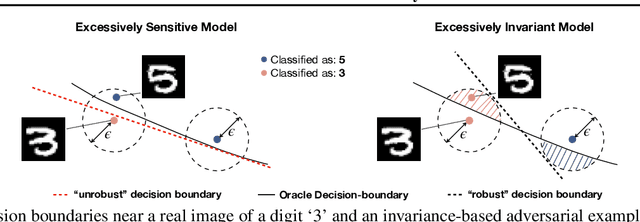
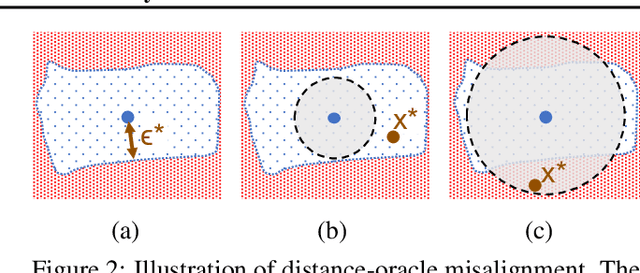
Adversarial examples are malicious inputs crafted to induce misclassification. Commonly studied sensitivity-based adversarial examples introduce semantically-small changes to an input that result in a different model prediction. This paper studies a complementary failure mode, invariance-based adversarial examples, that introduce minimal semantic changes that modify an input's true label yet preserve the model's prediction. We demonstrate fundamental tradeoffs between these two types of adversarial examples. We show that defenses against sensitivity-based attacks actively harm a model's accuracy on invariance-based attacks, and that new approaches are needed to resist both attack types. In particular, we break state-of-the-art adversarially-trained and certifiably-robust models by generating small perturbations that the models are (provably) robust to, yet that change an input's class according to human labelers. Finally, we formally show that the existence of excessively invariant classifiers arises from the presence of overly-robust predictive features in standard datasets.

Deep Relevance Regularization: Interpretable and Robust Tumor Typing of Imaging Mass Spectrometry Data

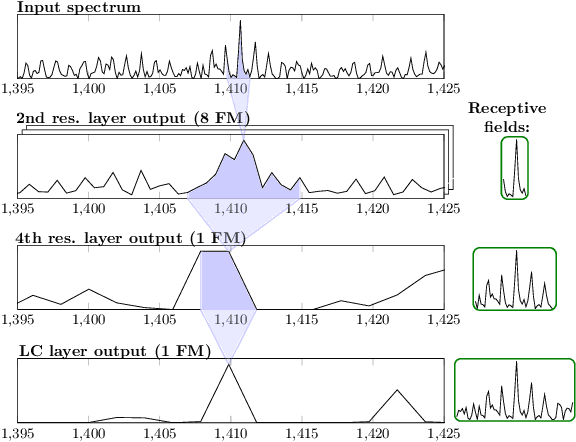
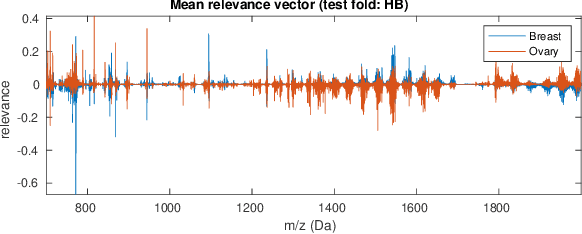
Neural networks have recently been established as a viable classification method for imaging mass spectrometry data for tumor typing. For multi-laboratory scenarios however, certain confounding factors may strongly impede their performance. In this work, we introduce Deep Relevance Regularization, a method of restricting what the neural network can focus on during classification, in order to improve the classification performance. We demonstrate how Deep Relevance Regularization robustifies neural networks against confounding factors on a challenging inter-lab dataset consisting of breast and ovarian carcinoma. We further show that this makes the relevance map -- a way of visualizing the discriminative parts of the mass spectrum -- sparser, thereby making the classifier easier to interpret

Residual Flows for Invertible Generative Modeling

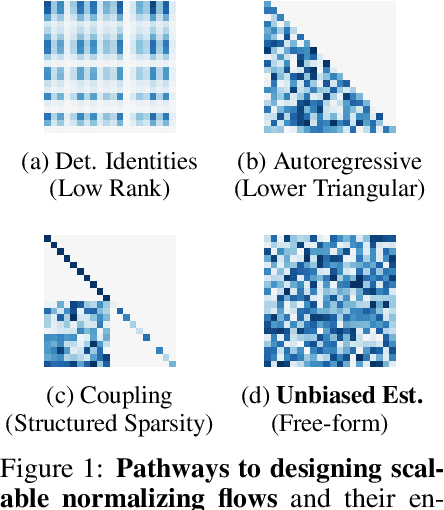
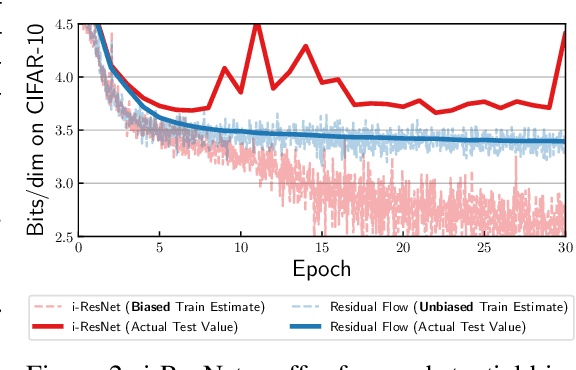
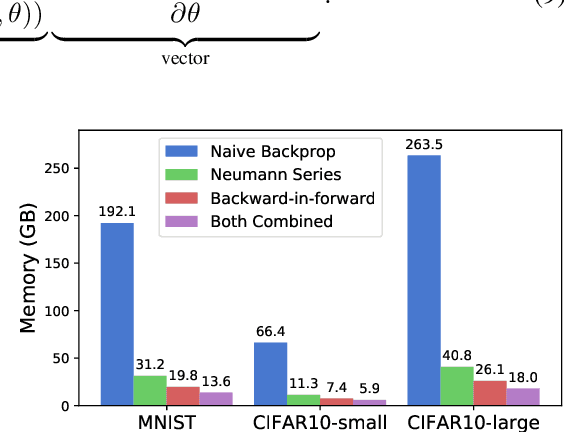
Flow-based generative models parameterize probability distributions through an invertible transformation and can be trained by maximum likelihood. Invertible residual networks provide a flexible family of transformations where only Lipschitz conditions rather than strict architectural constraints are needed for enforcing invertibility. However, prior work trained invertible residual networks for density estimation by relying on biased log-density estimates whose bias increased with the network's expressiveness. We give a tractable unbiased estimate of the log density, and reduce the memory required during training by a factor of ten. Furthermore, we improve invertible residual blocks by proposing the use of activation functions that avoid gradient saturation and generalizing the Lipschitz condition to induced mixed norms. The resulting approach, called Residual Flows, achieves state-of-the-art performance on density estimation amongst flow-based models, and outperforms networks that use coupling blocks at joint generative and discriminative modeling.

Invertible Residual Networks

Reversible deep networks provide useful theoretical guarantees and have proven to be a powerful class of functions in many applications. Usually, they rely on analytical inverses using dimension splitting, fundamentally constraining their structure compared to common architectures. Based on recent links between ordinary differential equations and deep networks, we provide a sufficient condition when standard ResNets are invertible. This condition allows unconstrained architectures for residual blocks, while only requiring an adaption to their regularization scheme. We numerically compute their inverse, which has O(1) memory cost and computational cost of 5-20 forward passes. Finally, we show that invertible ResNets perform on par with standard ResNets on classifying MNIST and CIFAR10 images.