Non-Uniform Diffusion Models

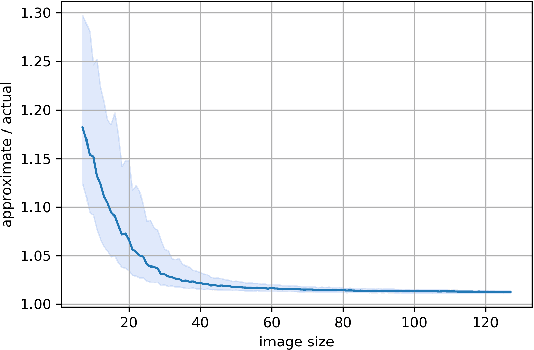
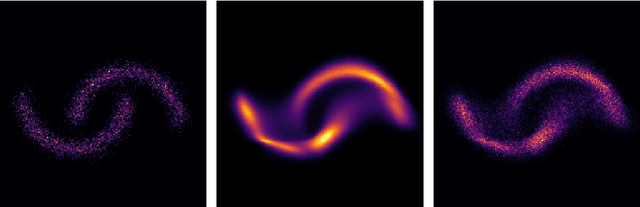
Diffusion models have emerged as one of the most promising frameworks for deep generative modeling. In this work, we explore the potential of non-uniform diffusion models. We show that non-uniform diffusion leads to multi-scale diffusion models which have similar structure to this of multi-scale normalizing flows. We experimentally find that in the same or less training time, the multi-scale diffusion model achieves better FID score than the standard uniform diffusion model. More importantly, it generates samples $4.4$ times faster in $128\times 128$ resolution. The speed-up is expected to be higher in higher resolutions where more scales are used. Moreover, we show that non-uniform diffusion leads to a novel estimator for the conditional score function which achieves on par performance with the state-of-the-art conditional denoising estimator. Our theoretical and experimental findings are accompanied by an open source library MSDiff which can facilitate further research of non-uniform diffusion models.

Conditional Image Generation with Score-Based Diffusion Models

Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling. In this work we conduct a systematic comparison and theoretical analysis of different approaches to learning conditional probability distributions with score-based diffusion models. In particular, we prove results which provide a theoretical justification for one of the most successful estimators of the conditional score. Moreover, we introduce a multi-speed diffusion framework, which leads to a new estimator for the conditional score, performing on par with previous state-of-the-art approaches. Our theoretical and experimental findings are accompanied by an open source library MSDiff which allows for application and further research of multi-speed diffusion models.

CAFLOW: Conditional Autoregressive Flows

We introduce CAFLOW, a new diverse image-to-image translation model that simultaneously leverages the power of auto-regressive modeling and the modeling efficiency of conditional normalizing flows. We transform the conditioning image into a sequence of latent encodings using a multi-scale normalizing flow and repeat the process for the conditioned image. We model the conditional distribution of the latent encodings by modeling the auto-regressive distributions with an efficient multi-scale normalizing flow, where each conditioning factor affects image synthesis at its respective resolution scale. Our proposed framework performs well on a range of image-to-image translation tasks. It outperforms former designs of conditional flows because of its expressive auto-regressive structure.

Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)

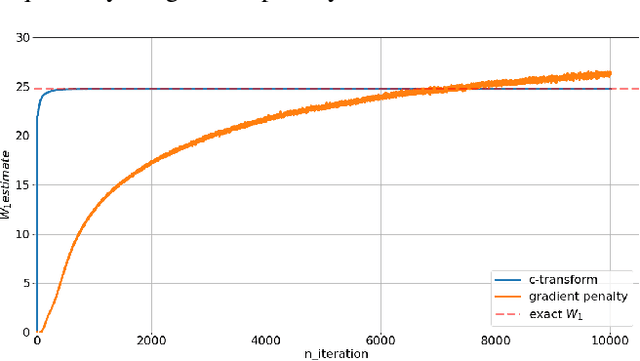
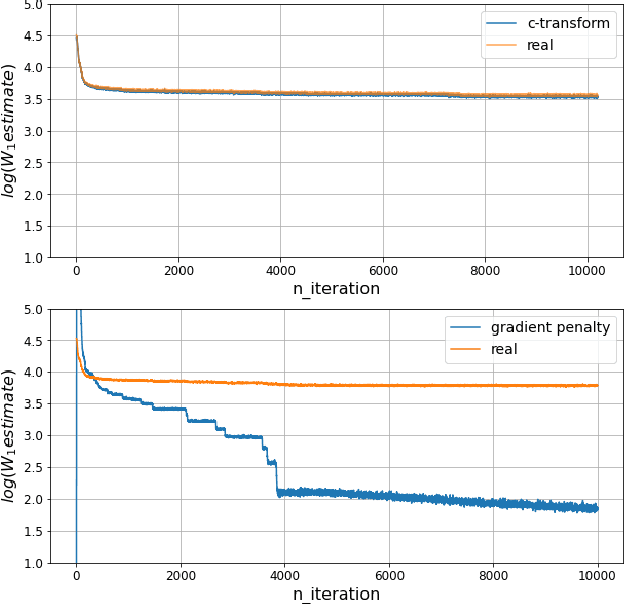
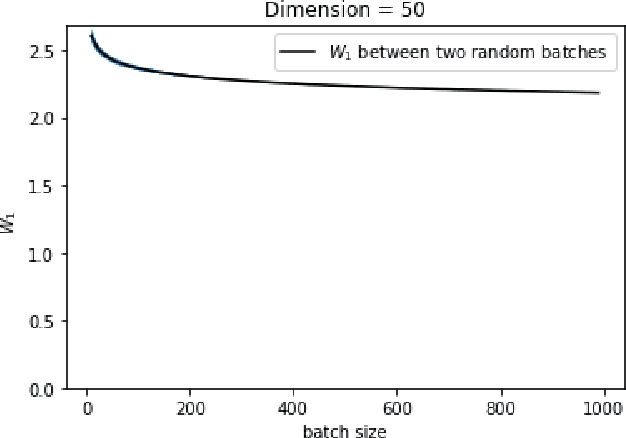
Wasserstein GANs are based on the idea of minimising the Wasserstein distance between a real and a generated distribution. We provide an in-depth mathematical analysis of differences between the theoretical setup and the reality of training Wasserstein GANs. In this work, we gather both theoretical and empirical evidence that the WGAN loss is not a meaningful approximation of the Wasserstein distance. Moreover, we argue that the Wasserstein distance is not even a desirable loss function for deep generative models, and conclude that the success of Wasserstein GANs can in truth be attributed to a failure to approximate the Wasserstein distance.

Equivariant neural networks for inverse problems

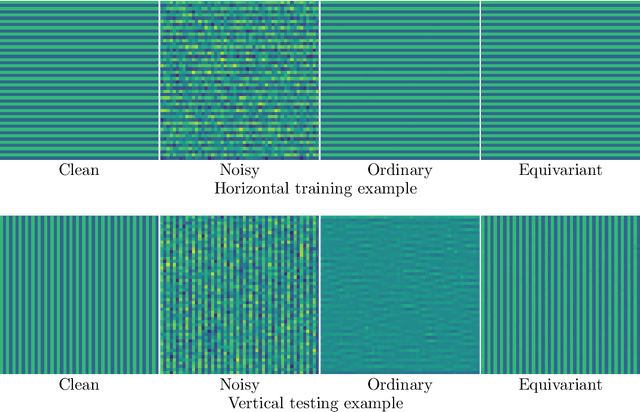
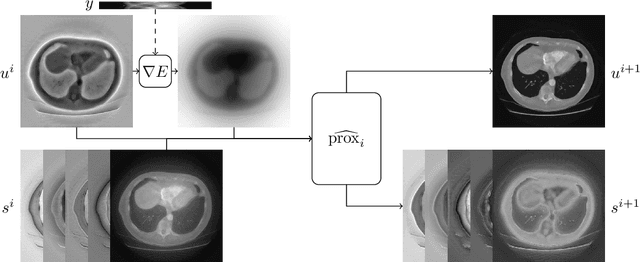
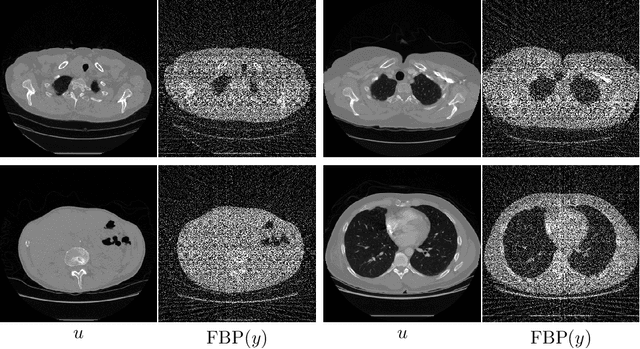
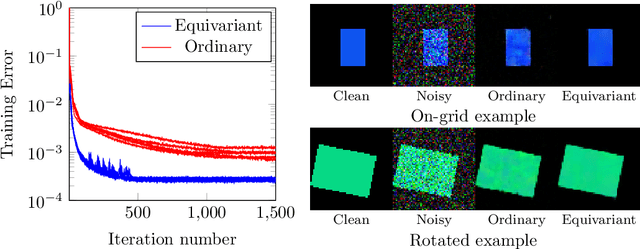
In recent years the use of convolutional layers to encode an inductive bias (translational equivariance) in neural networks has proven to be a very fruitful idea. The successes of this approach have motivated a line of research into incorporating other symmetries into deep learning methods, in the form of group equivariant convolutional neural networks. Much of this work has been focused on roto-translational symmetry of $\mathbf R^d$, but other examples are the scaling symmetry of $\mathbf R^d$ and rotational symmetry of the sphere. In this work, we demonstrate that group equivariant convolutional operations can naturally be incorporated into learned reconstruction methods for inverse problems that are motivated by the variational regularisation approach. Indeed, if the regularisation functional is invariant under a group symmetry, the corresponding proximal operator will satisfy an equivariance property with respect to the same group symmetry. As a result of this observation, we design learned iterative methods in which the proximal operators are modelled as group equivariant convolutional neural networks. We use roto-translationally equivariant operations in the proposed methodology and apply it to the problems of low-dose computerised tomography reconstruction and subsampled magnetic resonance imaging reconstruction. The proposed methodology is demonstrated to improve the reconstruction quality of a learned reconstruction method with a little extra computational cost at training time but without any extra cost at test time.

Depthwise Separable Convolutions Allow for Fast and Memory-Efficient Spectral Normalization

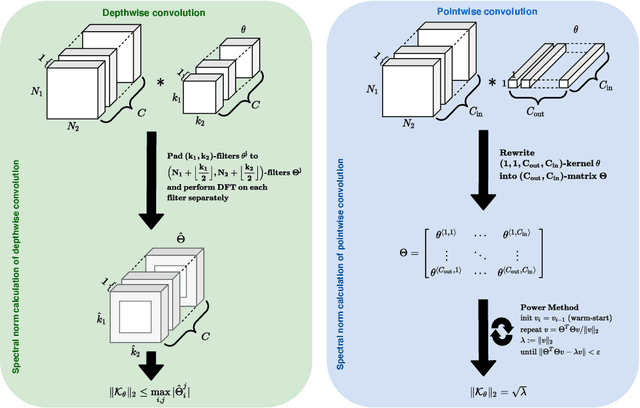
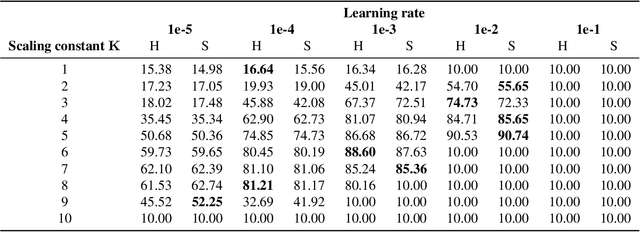
An increasing number of models require the control of the spectral norm of convolutional layers of a neural network. While there is an abundance of methods for estimating and enforcing upper bounds on those during training, they are typically costly in either memory or time. In this work, we introduce a very simple method for spectral normalization of depthwise separable convolutions, which introduces negligible computational and memory overhead. We demonstrate the effectiveness of our method on image classification tasks using standard architectures like MobileNetV2.

Machine learning for COVID-19 detection and prognostication using chest radiographs and CT scans: a systematic methodological review

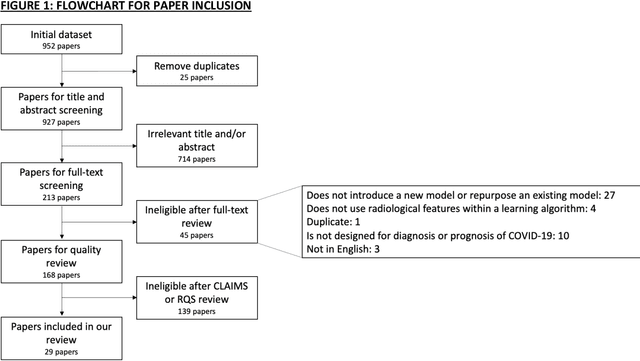
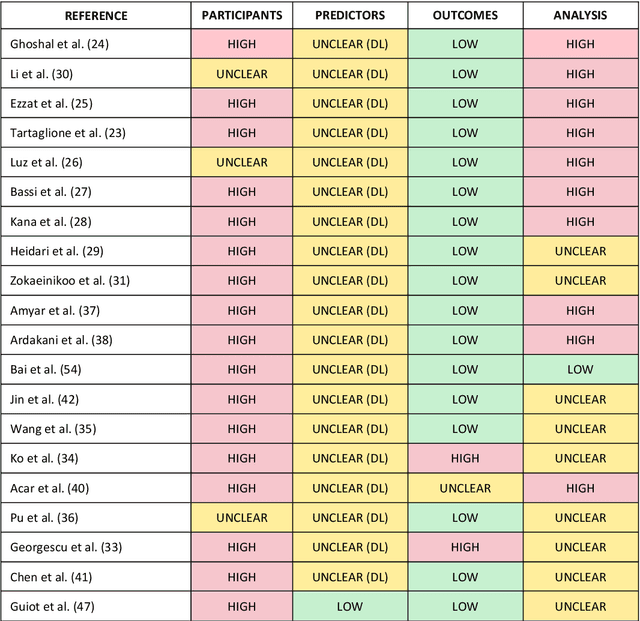
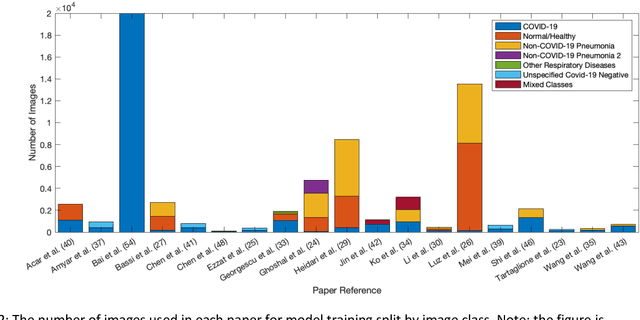
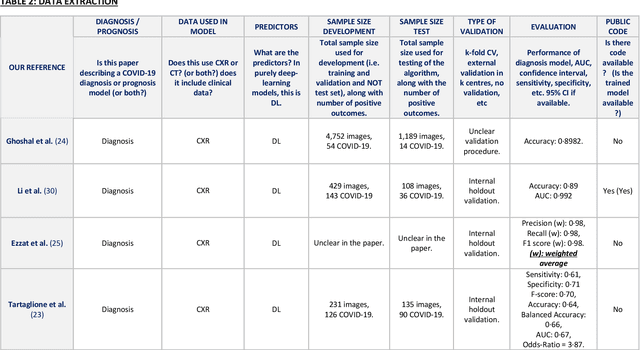
Background: Machine learning methods offer great potential for fast and accurate detection and prognostication of COVID-19 from standard-of-care chest radiographs (CXR) and computed tomography (CT) images. In this systematic review we critically evaluate the machine learning methodologies employed in the rapidly growing literature. Methods: In this systematic review we reviewed EMBASE via OVID, MEDLINE via PubMed, bioRxiv, medRxiv and arXiv for published papers and preprints uploaded from Jan 1, 2020 to June 24, 2020. Studies which consider machine learning models for the diagnosis or prognosis of COVID-19 from CXR or CT images were included. A methodology quality review of each paper was performed against established benchmarks to ensure the review focusses only on high-quality reproducible papers. This study is registered with PROSPERO [CRD42020188887]. Interpretation: Our review finds that none of the developed models discussed are of potential clinical use due to methodological flaws and underlying biases. This is a major weakness, given the urgency with which validated COVID-19 models are needed. Typically, we find that the documentation of a model's development is not sufficient to make the results reproducible and therefore of 168 candidate papers only 29 are deemed to be reproducible and subsequently considered in this review. We therefore encourage authors to use established machine learning checklists to ensure sufficient documentation is made available, and to follow the PROBAST (prediction model risk of bias assessment tool) framework to determine the underlying biases in their model development process and to mitigate these where possible. This is key to safe clinical implementation which is urgently needed.

iUNets: Fully invertible U-Nets with Learnable Up- and Downsampling

U-Nets have been established as a standard architecture for image-to-image learning problems such as segmentation and inverse problems in imaging. For large-scale data, as it for example appears in 3D medical imaging, the U-Net however has prohibitive memory requirements. Here, we present a new fully-invertible U-Net-based architecture called the iUNet, which employs novel learnable and invertible up- and downsampling operations, thereby making the use of memory-efficient backpropagation possible. This allows us to train deeper and larger networks in practice, under the same GPU memory restrictions. Due to its invertibility, the iUNet can furthermore be used for constructing normalizing flows.

Structure preserving deep learning

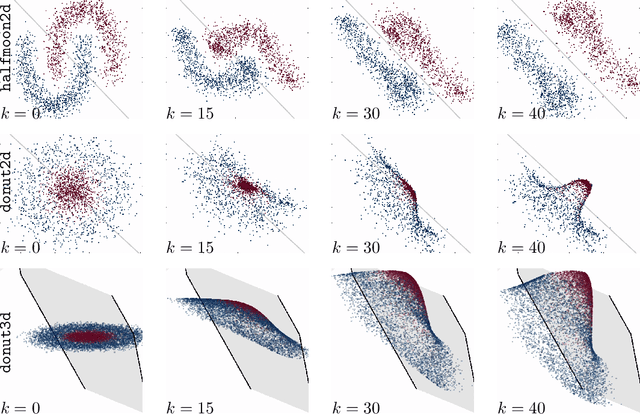
Over the past few years, deep learning has risen to the foreground as a topic of massive interest, mainly as a result of successes obtained in solving large-scale image processing tasks. There are multiple challenging mathematical problems involved in applying deep learning: most deep learning methods require the solution of hard optimisation problems, and a good understanding of the tradeoff between computational effort, amount of data and model complexity is required to successfully design a deep learning approach for a given problem. A large amount of progress made in deep learning has been based on heuristic explorations, but there is a growing effort to mathematically understand the structure in existing deep learning methods and to systematically design new deep learning methods to preserve certain types of structure in deep learning. In this article, we review a number of these directions: some deep neural networks can be understood as discretisations of dynamical systems, neural networks can be designed to have desirable properties such as invertibility or group equivariance, and new algorithmic frameworks based on conformal Hamiltonian systems and Riemannian manifolds to solve the optimisation problems have been proposed. We conclude our review of each of these topics by discussing some open problems that we consider to be interesting directions for future research.

Deep Relevance Regularization: Interpretable and Robust Tumor Typing of Imaging Mass Spectrometry Data

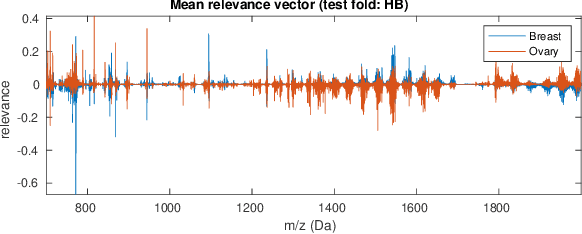
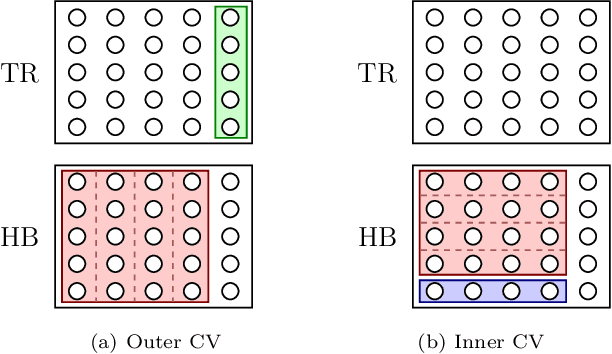
Neural networks have recently been established as a viable classification method for imaging mass spectrometry data for tumor typing. For multi-laboratory scenarios however, certain confounding factors may strongly impede their performance. In this work, we introduce Deep Relevance Regularization, a method of restricting what the neural network can focus on during classification, in order to improve the classification performance. We demonstrate how Deep Relevance Regularization robustifies neural networks against confounding factors on a challenging inter-lab dataset consisting of breast and ovarian carcinoma. We further show that this makes the relevance map -- a way of visualizing the discriminative parts of the mass spectrum -- sparser, thereby making the classifier easier to interpret