Parallel-in-Time Solutions with Random Projection Neural Networks

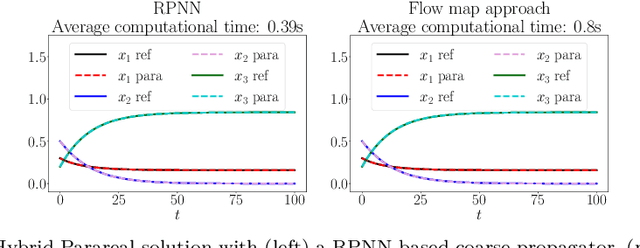
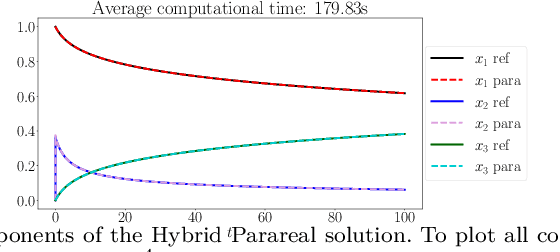
This paper considers one of the fundamental parallel-in-time methods for the solution of ordinary differential equations, Parareal, and extends it by adopting a neural network as a coarse propagator. We provide a theoretical analysis of the convergence properties of the proposed algorithm and show its effectiveness for several examples, including Lorenz and Burgers' equations. In our numerical simulations, we further specialize the underpinning neural architecture to Random Projection Neural Networks (RPNNs), a 2-layer neural network where the first layer weights are drawn at random rather than optimized. This restriction substantially increases the efficiency of fitting RPNN's weights in comparison to a standard feedforward network without negatively impacting the accuracy, as demonstrated in the SIR system example.

Equidistribution-based training of Free Knot Splines and ReLU Neural Networks

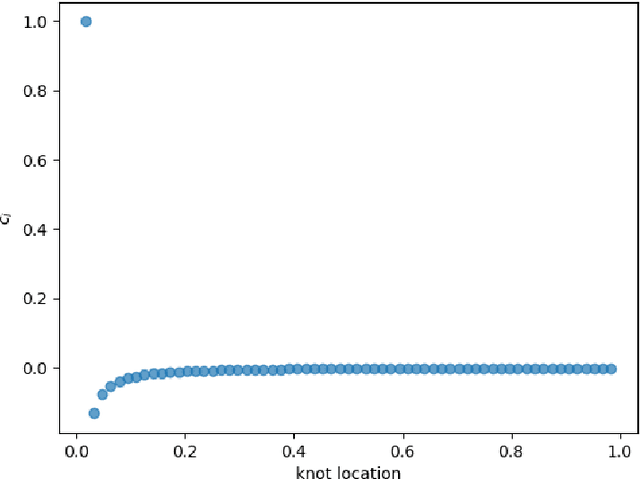
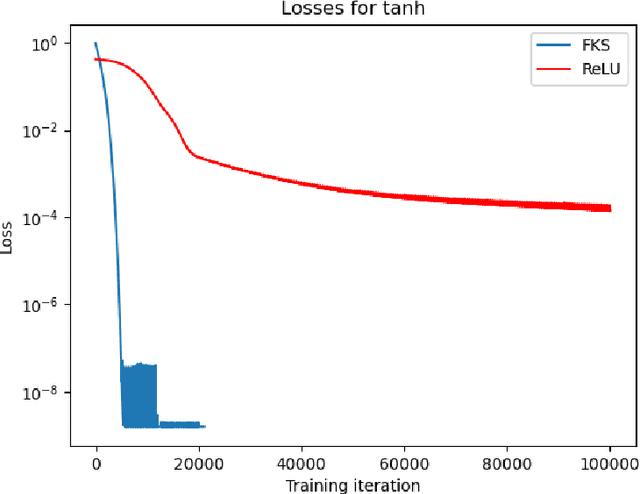
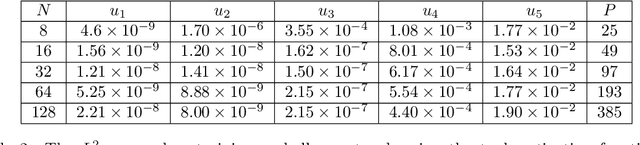
We consider the problem of one-dimensional function approximation using shallow neural networks (NN) with a rectified linear unit (ReLU) activation function and compare their training with traditional methods such as univariate Free Knot Splines (FKS). ReLU NNs and FKS span the same function space, and thus have the same theoretical expressivity. In the case of ReLU NNs, we show that their ill-conditioning degrades rapidly as the width of the network increases. This often leads to significantly poorer approximation in contrast to the FKS representation, which remains well-conditioned as the number of knots increases. We leverage the theory of optimal piecewise linear interpolants to improve the training procedure for a ReLU NN. Using the equidistribution principle, we propose a two-level procedure for training the FKS by first solving the nonlinear problem of finding the optimal knot locations of the interpolating FKS. Determining the optimal knots then acts as a good starting point for training the weights of the FKS. The training of the FKS gives insights into how we can train a ReLU NN effectively to give an equally accurate approximation. More precisely, we combine the training of the ReLU NN with an equidistribution based loss to find the breakpoints of the ReLU functions, combined with preconditioning the ReLU NN approximation (to take an FKS form) to find the scalings of the ReLU functions, leads to a well-conditioned and reliable method of finding an accurate ReLU NN approximation to a target function. We test this method on a series or regular, singular, and rapidly varying target functions and obtain good results realising the expressivity of the network in this case.

Closing the ODE-SDE gap in score-based diffusion models through the Fokker-Planck equation

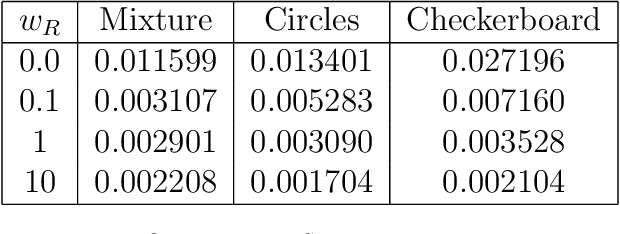
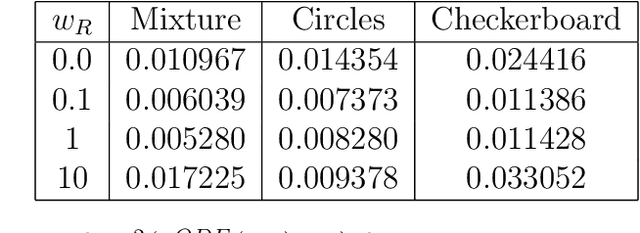
Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling, due to their state-of-the art performance in many generation tasks while relying on mathematical foundations such as stochastic differential equations (SDEs) and ordinary differential equations (ODEs). Empirically, it has been reported that ODE based samples are inferior to SDE based samples. In this paper we rigorously describe the range of dynamics and approximations that arise when training score-based diffusion models, including the true SDE dynamics, the neural approximations, the various approximate particle dynamics that result, as well as their associated Fokker--Planck equations and the neural network approximations of these Fokker--Planck equations. We systematically analyse the difference between the ODE and SDE dynamics of score-based diffusion models, and link it to an associated Fokker--Planck equation. We derive a theoretical upper bound on the Wasserstein 2-distance between the ODE- and SDE-induced distributions in terms of a Fokker--Planck residual. We also show numerically that conventional score-based diffusion models can exhibit significant differences between ODE- and SDE-induced distributions which we demonstrate using explicit comparisons. Moreover, we show numerically that reducing the Fokker--Planck residual by adding it as an additional regularisation term leads to closing the gap between ODE- and SDE-induced distributions. Our experiments suggest that this regularisation can improve the distribution generated by the ODE, however that this can come at the cost of degraded SDE sample quality.

Models for information propagation on graphs

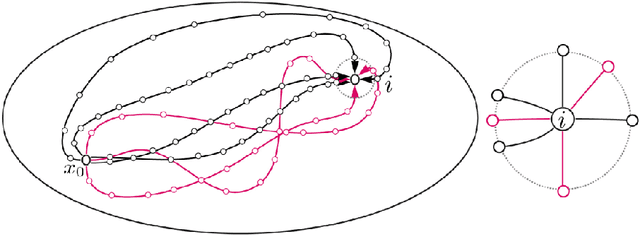
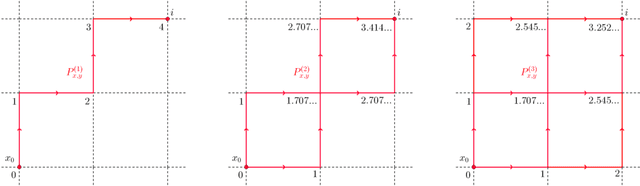
In this work we propose and unify classes of different models for information propagation over graphs. In a first class, propagation is modeled as a wave which emanates from a set of known nodes at an initial time, to all other unknown nodes at later times with an ordering determined by the time at which the information wave front reaches nodes. A second class of models is based on the notion of a travel time along paths between nodes. The time of information propagation from an initial known set of nodes to a node is defined as the minimum of a generalized travel time over subsets of all admissible paths. A final class is given by imposing a local equation of an eikonal form at each unknown node, with boundary conditions at the known nodes. The solution value of the local equation at a node is coupled the neighbouring nodes with smaller solution values. We provide precise formulations of the model classes in this graph setting, and prove equivalences between them. Motivated by the connection between first arrival time model and the eikonal equation in the continuum setting, we demonstrate that for graphs in the particular form of grids in Euclidean space mean field limits under grid refinement of certain graph models lead to Hamilton-Jacobi PDEs. For a specific parameter setting, we demonstrate that the solution on the grid approximates the Euclidean distance.

Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)

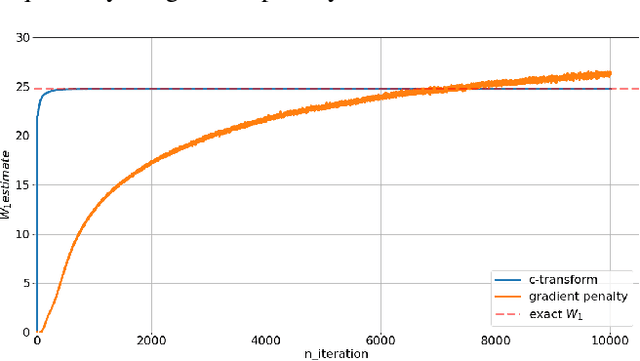
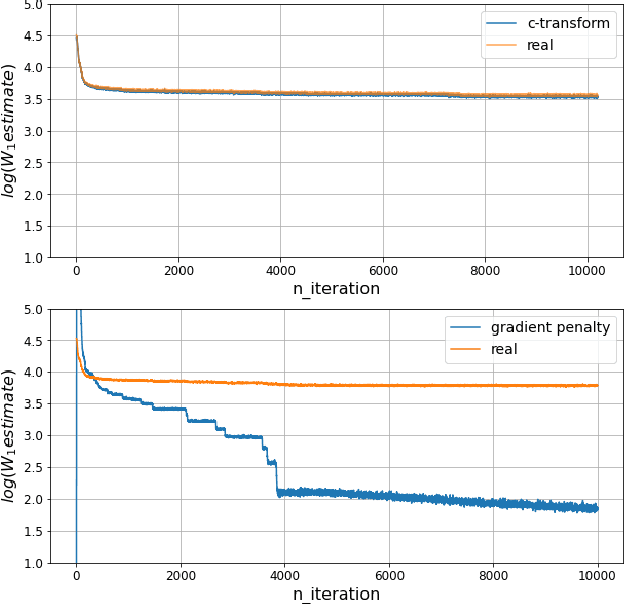
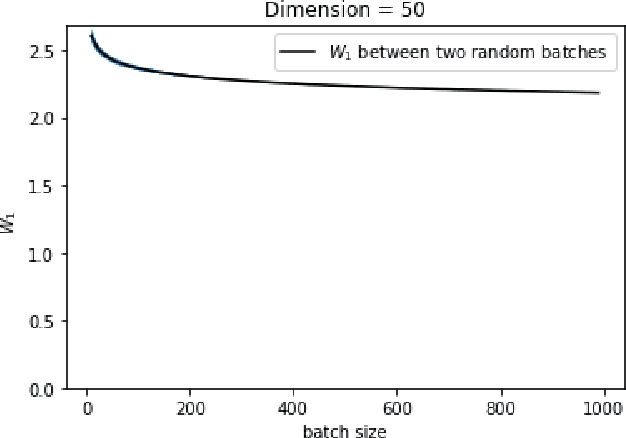
Wasserstein GANs are based on the idea of minimising the Wasserstein distance between a real and a generated distribution. We provide an in-depth mathematical analysis of differences between the theoretical setup and the reality of training Wasserstein GANs. In this work, we gather both theoretical and empirical evidence that the WGAN loss is not a meaningful approximation of the Wasserstein distance. Moreover, we argue that the Wasserstein distance is not even a desirable loss function for deep generative models, and conclude that the success of Wasserstein GANs can in truth be attributed to a failure to approximate the Wasserstein distance.

On anisotropic diffusion equations for label propagation

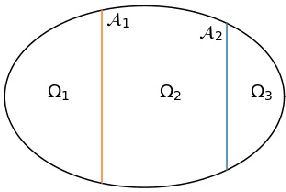
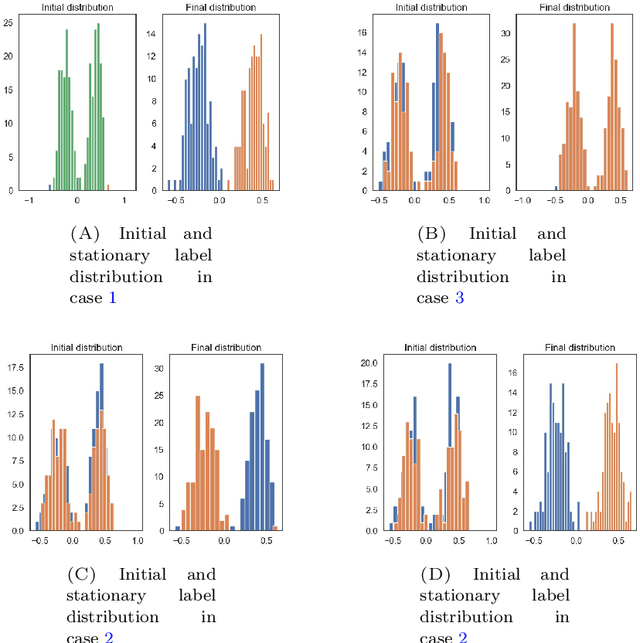
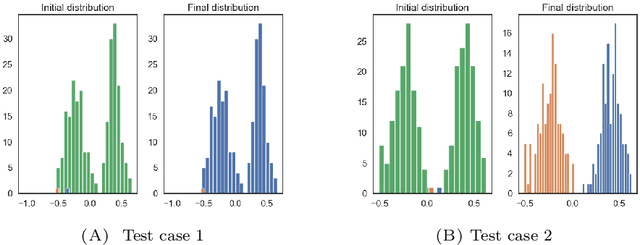
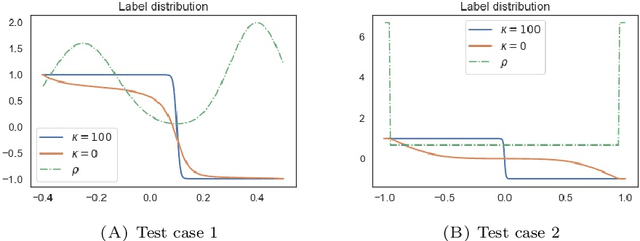
In many problems in data classification one wishes to assign labels to points in a point cloud with a certain number of them being already correctly labeled. In this paper, we propose a microscopic ODE approach, in which information about correct labels is propagated to neighboring points. Its dynamics are based on alignment mechanisms, which are often used in collective and consensus models. We derive the respective continuum description, which corresponds to an anisotropic diffusion equation with reaction term. Solutions of the continuum model inherit interesting properties of the underlying point cloud. We discuss these analytic properties and exemplify the results with micro- and macroscopic simulations.

A Deterministic Approach to Avoid Saddle Points

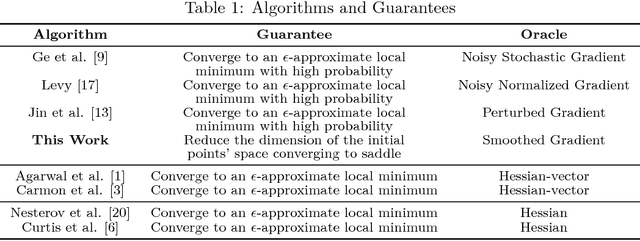
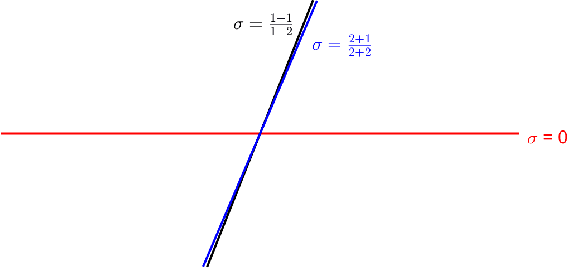
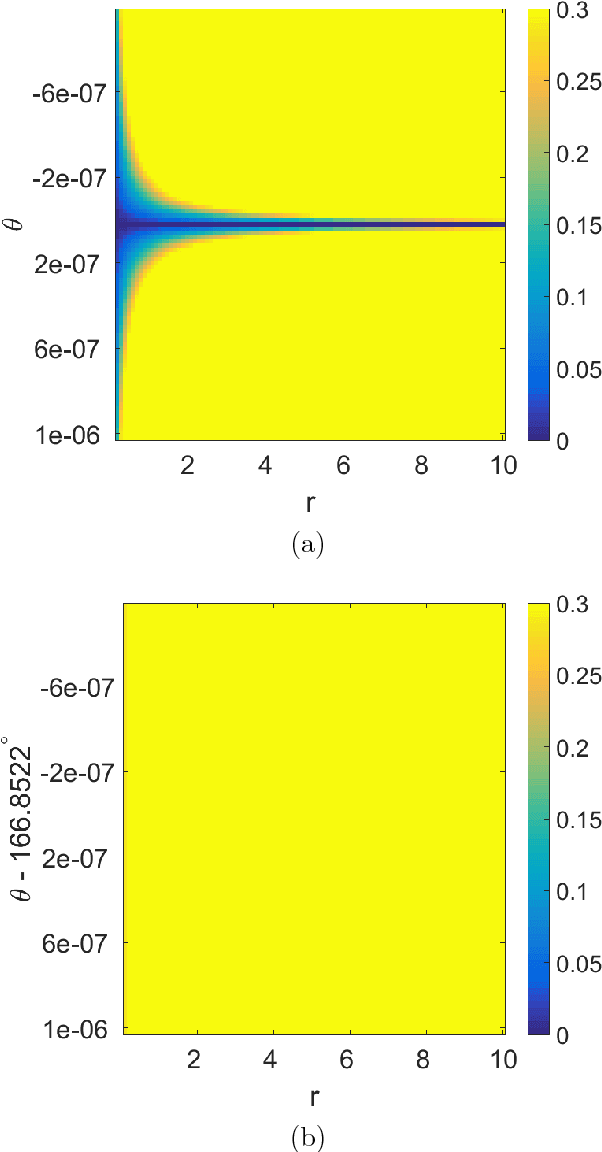
Loss functions with a large number of saddle points are one of the main obstacles to training many modern machine learning models. Gradient descent (GD) is a fundamental algorithm for machine learning and converges to a saddle point for certain initial data. We call the region formed by these initial values the "attraction region." For quadratic functions, GD converges to a saddle point if the initial data is in a subspace of up to n-1 dimensions. In this paper, we prove that a small modification of the recently proposed Laplacian smoothing gradient descent (LSGD) [Osher, et al., arXiv:1806.06317] contributes to avoiding saddle points without sacrificing the convergence rate of GD. In particular, we show that the dimension of the LSGD's attraction region is at most floor((n-1)/2) for a class of quadratic functions which is significantly smaller than GD's (n-1)-dimensional attraction region.