A Deterministic Approach to Avoid Saddle Points
Paper and Code
Jan 21, 2019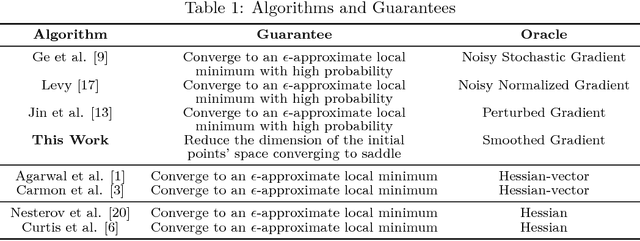
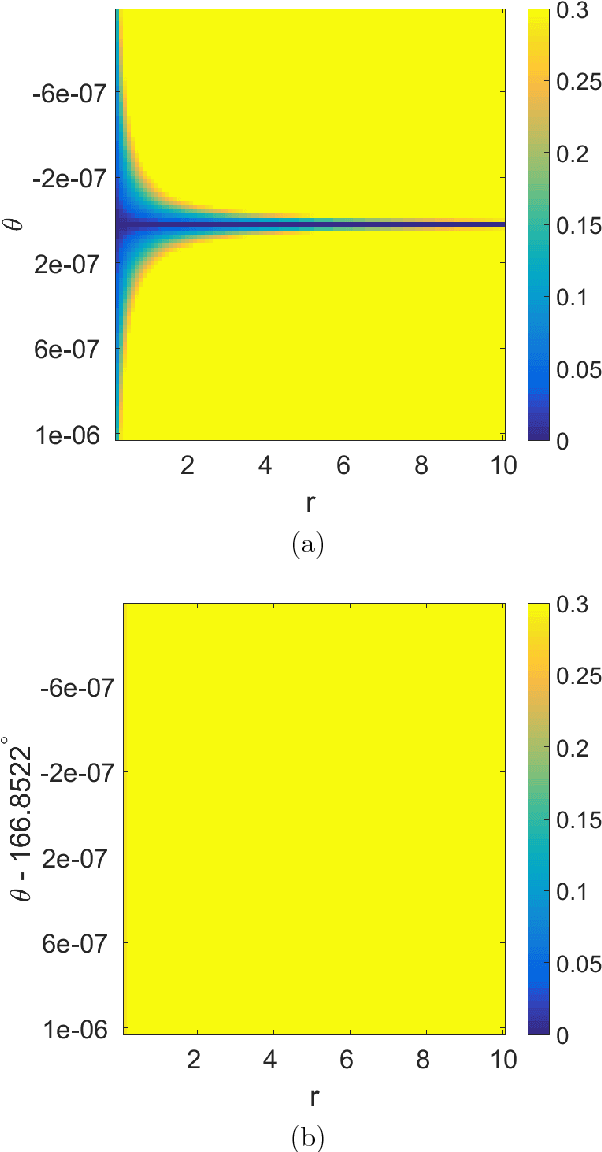
Loss functions with a large number of saddle points are one of the main obstacles to training many modern machine learning models. Gradient descent (GD) is a fundamental algorithm for machine learning and converges to a saddle point for certain initial data. We call the region formed by these initial values the "attraction region." For quadratic functions, GD converges to a saddle point if the initial data is in a subspace of up to n-1 dimensions. In this paper, we prove that a small modification of the recently proposed Laplacian smoothing gradient descent (LSGD) [Osher, et al., arXiv:1806.06317] contributes to avoiding saddle points without sacrificing the convergence rate of GD. In particular, we show that the dimension of the LSGD's attraction region is at most floor((n-1)/2) for a class of quadratic functions which is significantly smaller than GD's (n-1)-dimensional attraction region.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge