Models for information propagation on graphs
Paper and Code
Jan 19, 2022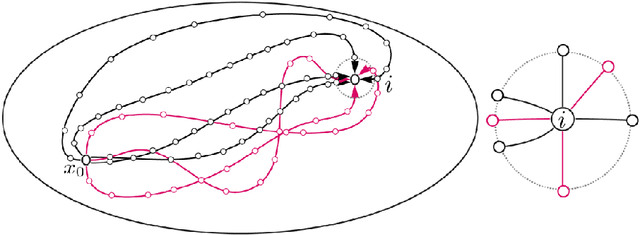

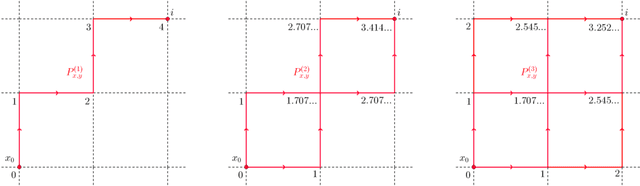

In this work we propose and unify classes of different models for information propagation over graphs. In a first class, propagation is modeled as a wave which emanates from a set of known nodes at an initial time, to all other unknown nodes at later times with an ordering determined by the time at which the information wave front reaches nodes. A second class of models is based on the notion of a travel time along paths between nodes. The time of information propagation from an initial known set of nodes to a node is defined as the minimum of a generalized travel time over subsets of all admissible paths. A final class is given by imposing a local equation of an eikonal form at each unknown node, with boundary conditions at the known nodes. The solution value of the local equation at a node is coupled the neighbouring nodes with smaller solution values. We provide precise formulations of the model classes in this graph setting, and prove equivalences between them. Motivated by the connection between first arrival time model and the eikonal equation in the continuum setting, we demonstrate that for graphs in the particular form of grids in Euclidean space mean field limits under grid refinement of certain graph models lead to Hamilton-Jacobi PDEs. For a specific parameter setting, we demonstrate that the solution on the grid approximates the Euclidean distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge