Hyperparameter Optimization for Randomized Algorithms: A Case Study for Random Features

Randomized algorithms exploit stochasticity to reduce computational complexity. One important example is random feature regression (RFR) that accelerates Gaussian process regression (GPR). RFR approximates an unknown function with a random neural network whose hidden weights and biases are sampled from a probability distribution. Only the final output layer is fit to data. In randomized algorithms like RFR, the hyperparameters that characterize the sampling distribution greatly impact performance, yet are not directly accessible from samples. This makes optimization of hyperparameters via standard (gradient-based) optimization tools inapplicable. Inspired by Bayesian ideas from GPR, this paper introduces a random objective function that is tailored for hyperparameter tuning of vector-valued random features. The objective is minimized with ensemble Kalman inversion (EKI). EKI is a gradient-free particle-based optimizer that is scalable to high-dimensions and robust to randomness in objective functions. A numerical study showcases the new black-box methodology to learn hyperparameter distributions in several problems that are sensitive to the hyperparameter selection: two global sensitivity analyses, integrating a chaotic dynamical system, and solving a Bayesian inverse problem from atmospheric dynamics. The success of the proposed EKI-based algorithm for RFR suggests its potential for automated optimization of hyperparameters arising in other randomized algorithms.

Toward Routing River Water in Land Surface Models with Recurrent Neural Networks

Machine learning is playing an increasing role in hydrology, supplementing or replacing physics-based models. One notable example is the use of recurrent neural networks (RNNs) for forecasting streamflow given observed precipitation and geographic characteristics. Training of such a model over the continental United States has demonstrated that a single set of model parameters can be used across independent catchments, and that RNNs can outperform physics-based models. In this work, we take a next step and study the performance of RNNs for river routing in land surface models (LSMs). Instead of observed precipitation, the LSM-RNN uses instantaneous runoff calculated from physics-based models as an input. We train the model with data from river basins spanning the globe and test it in streamflow hindcasts. The model demonstrates skill at generalization across basins (predicting streamflow in unseen catchments) and across time (predicting streamflow during years not used in training). We compare the predictions from the LSM-RNN to an existing physics-based model calibrated with a similar dataset and find that the LSM-RNN outperforms the physics-based model. Our results give further evidence that RNNs are effective for global streamflow prediction from runoff inputs and motivate the development of complete routing models that can capture nested sub-basis connections.

Models for information propagation on graphs

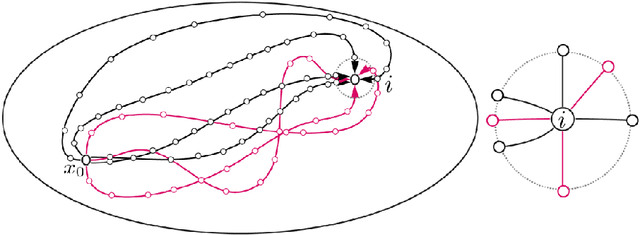
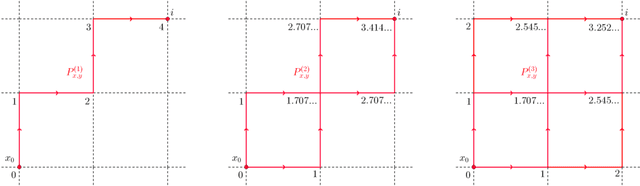
In this work we propose and unify classes of different models for information propagation over graphs. In a first class, propagation is modeled as a wave which emanates from a set of known nodes at an initial time, to all other unknown nodes at later times with an ordering determined by the time at which the information wave front reaches nodes. A second class of models is based on the notion of a travel time along paths between nodes. The time of information propagation from an initial known set of nodes to a node is defined as the minimum of a generalized travel time over subsets of all admissible paths. A final class is given by imposing a local equation of an eikonal form at each unknown node, with boundary conditions at the known nodes. The solution value of the local equation at a node is coupled the neighbouring nodes with smaller solution values. We provide precise formulations of the model classes in this graph setting, and prove equivalences between them. Motivated by the connection between first arrival time model and the eikonal equation in the continuum setting, we demonstrate that for graphs in the particular form of grids in Euclidean space mean field limits under grid refinement of certain graph models lead to Hamilton-Jacobi PDEs. For a specific parameter setting, we demonstrate that the solution on the grid approximates the Euclidean distance.