Equidistribution-based training of Free Knot Splines and ReLU Neural Networks
Paper and Code
Jul 02, 2024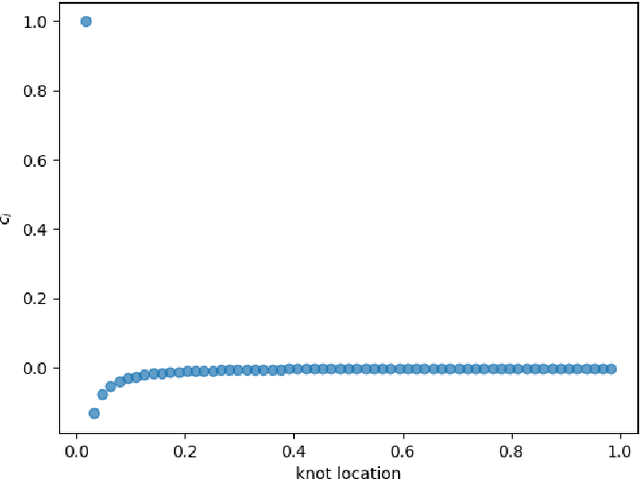

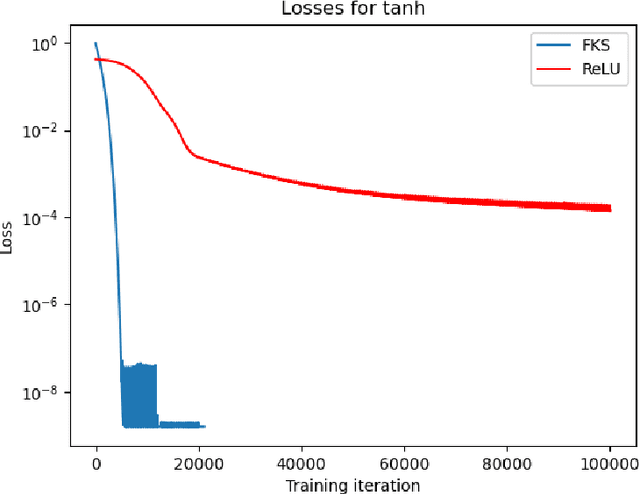
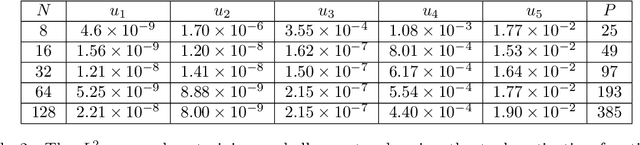
We consider the problem of one-dimensional function approximation using shallow neural networks (NN) with a rectified linear unit (ReLU) activation function and compare their training with traditional methods such as univariate Free Knot Splines (FKS). ReLU NNs and FKS span the same function space, and thus have the same theoretical expressivity. In the case of ReLU NNs, we show that their ill-conditioning degrades rapidly as the width of the network increases. This often leads to significantly poorer approximation in contrast to the FKS representation, which remains well-conditioned as the number of knots increases. We leverage the theory of optimal piecewise linear interpolants to improve the training procedure for a ReLU NN. Using the equidistribution principle, we propose a two-level procedure for training the FKS by first solving the nonlinear problem of finding the optimal knot locations of the interpolating FKS. Determining the optimal knots then acts as a good starting point for training the weights of the FKS. The training of the FKS gives insights into how we can train a ReLU NN effectively to give an equally accurate approximation. More precisely, we combine the training of the ReLU NN with an equidistribution based loss to find the breakpoints of the ReLU functions, combined with preconditioning the ReLU NN approximation (to take an FKS form) to find the scalings of the ReLU functions, leads to a well-conditioned and reliable method of finding an accurate ReLU NN approximation to a target function. We test this method on a series or regular, singular, and rapidly varying target functions and obtain good results realising the expressivity of the network in this case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge