G-Adaptive mesh refinement -- leveraging graph neural networks and differentiable finite element solvers

We present a novel, and effective, approach to the long-standing problem of mesh adaptivity in finite element methods (FEM). FE solvers are powerful tools for solving partial differential equations (PDEs), but their cost and accuracy are critically dependent on the choice of mesh points. To keep computational costs low, mesh relocation (r-adaptivity) seeks to optimise the position of a fixed number of mesh points to obtain the best FE solution accuracy. Classical approaches to this problem require the solution of a separate nonlinear "meshing" PDE to find the mesh point locations. This incurs significant cost at remeshing and relies on certain a-priori assumptions and guiding heuristics for optimal mesh point location. Recent machine learning approaches to r-adaptivity have mainly focused on the construction of fast surrogates for such classical methods. Our new approach combines a graph neural network (GNN) powered architecture, with training based on direct minimisation of the FE solution error with respect to the mesh point locations. The GNN employs graph neural diffusion (GRAND), closely aligning the mesh solution space to that of classical meshing methodologies, thus replacing heuristics with a learnable strategy, and providing a strong inductive bias. This allows for rapid and robust training and results in an extremely efficient and effective GNN approach to online r-adaptivity. This method outperforms classical and prior ML approaches to r-adaptive meshing on the test problems we consider, in particular achieving lower FE solution error, whilst retaining the significant speed-up over classical methods observed in prior ML work.

Equidistribution-based training of Free Knot Splines and ReLU Neural Networks

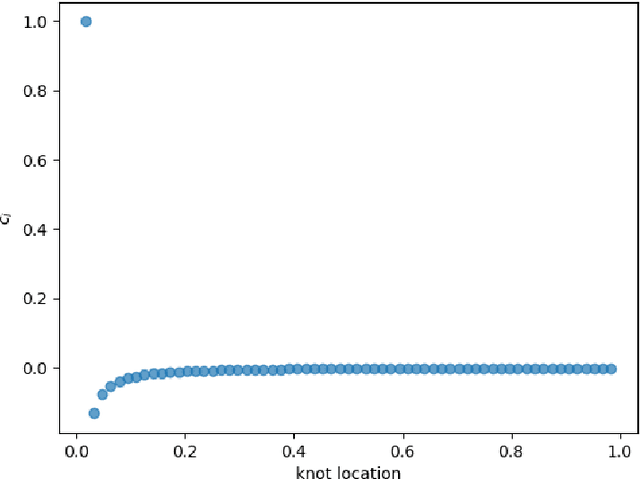
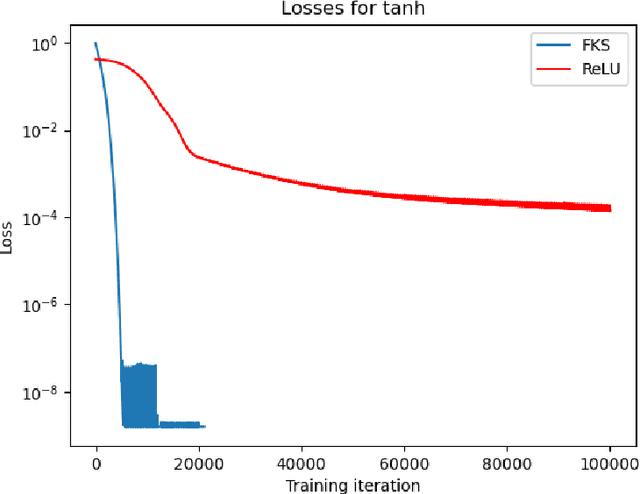
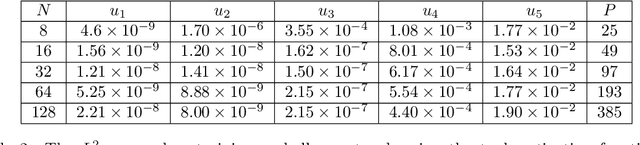
We consider the problem of one-dimensional function approximation using shallow neural networks (NN) with a rectified linear unit (ReLU) activation function and compare their training with traditional methods such as univariate Free Knot Splines (FKS). ReLU NNs and FKS span the same function space, and thus have the same theoretical expressivity. In the case of ReLU NNs, we show that their ill-conditioning degrades rapidly as the width of the network increases. This often leads to significantly poorer approximation in contrast to the FKS representation, which remains well-conditioned as the number of knots increases. We leverage the theory of optimal piecewise linear interpolants to improve the training procedure for a ReLU NN. Using the equidistribution principle, we propose a two-level procedure for training the FKS by first solving the nonlinear problem of finding the optimal knot locations of the interpolating FKS. Determining the optimal knots then acts as a good starting point for training the weights of the FKS. The training of the FKS gives insights into how we can train a ReLU NN effectively to give an equally accurate approximation. More precisely, we combine the training of the ReLU NN with an equidistribution based loss to find the breakpoints of the ReLU functions, combined with preconditioning the ReLU NN approximation (to take an FKS form) to find the scalings of the ReLU functions, leads to a well-conditioned and reliable method of finding an accurate ReLU NN approximation to a target function. We test this method on a series or regular, singular, and rapidly varying target functions and obtain good results realising the expressivity of the network in this case.

Closing the ODE-SDE gap in score-based diffusion models through the Fokker-Planck equation

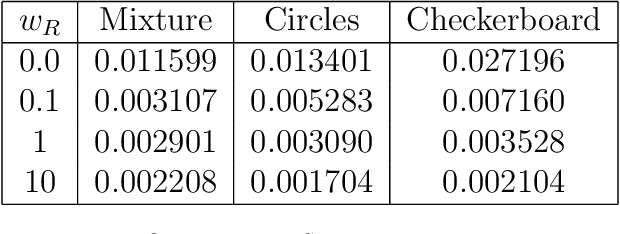
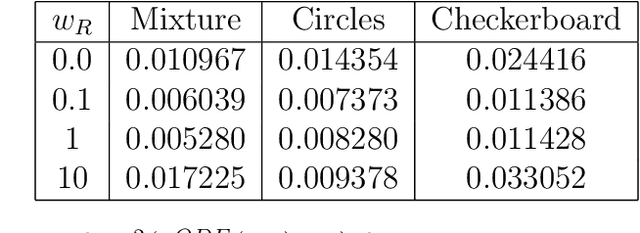
Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling, due to their state-of-the art performance in many generation tasks while relying on mathematical foundations such as stochastic differential equations (SDEs) and ordinary differential equations (ODEs). Empirically, it has been reported that ODE based samples are inferior to SDE based samples. In this paper we rigorously describe the range of dynamics and approximations that arise when training score-based diffusion models, including the true SDE dynamics, the neural approximations, the various approximate particle dynamics that result, as well as their associated Fokker--Planck equations and the neural network approximations of these Fokker--Planck equations. We systematically analyse the difference between the ODE and SDE dynamics of score-based diffusion models, and link it to an associated Fokker--Planck equation. We derive a theoretical upper bound on the Wasserstein 2-distance between the ODE- and SDE-induced distributions in terms of a Fokker--Planck residual. We also show numerically that conventional score-based diffusion models can exhibit significant differences between ODE- and SDE-induced distributions which we demonstrate using explicit comparisons. Moreover, we show numerically that reducing the Fokker--Planck residual by adding it as an additional regularisation term leads to closing the gap between ODE- and SDE-induced distributions. Our experiments suggest that this regularisation can improve the distribution generated by the ODE, however that this can come at the cost of degraded SDE sample quality.

Deep surrogate accelerated delayed-acceptance HMC for Bayesian inference of spatio-temporal heat fluxes in rotating disc systems

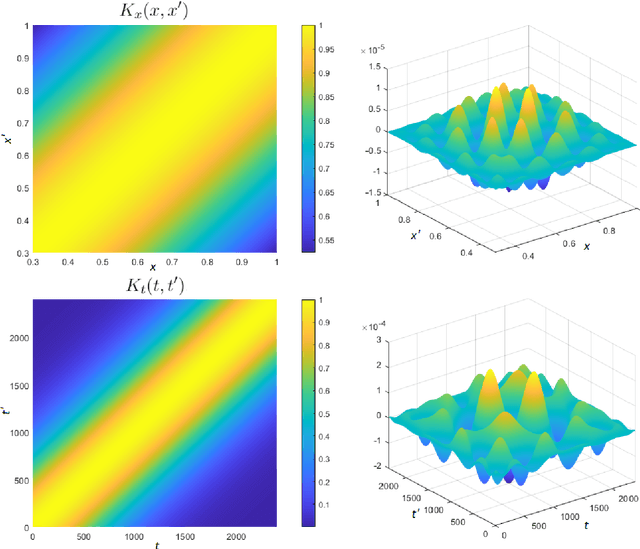
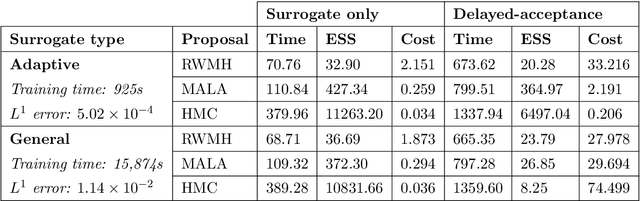
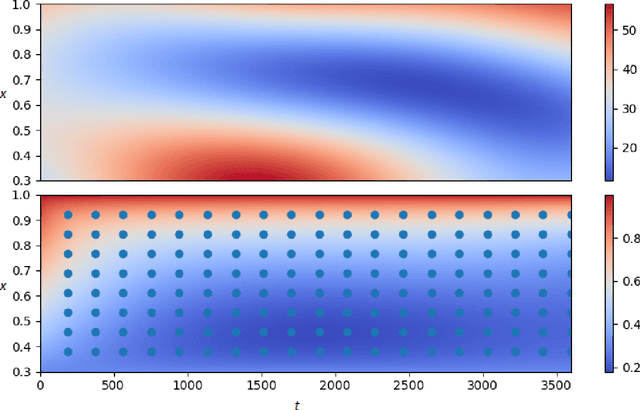
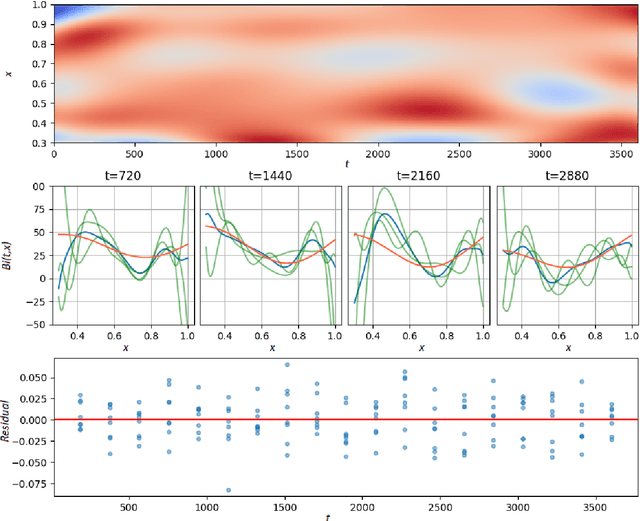
We study the Bayesian inverse problem of inferring the Biot number, a spatio-temporal heat-flux parameter in a PDE model. This is an ill-posed problem where standard optimisation yields unphysical inferences. We introduce a training scheme that uses temperature data to adaptively train a neural-network surrogate to simulate the parametric forward model. This approach approximates forward and inverse solution together, by simultaneously identifying an approximate posterior distribution over the Biot number, and weighting the forward training loss according to this approximation. Utilising random Chebyshev series, we outline how to approximate an arbitrary Gaussian process prior, and using the surrogate we apply Hamiltonian Monte Carlo (HMC) to efficiently sample from the corresponding posterior distribution. We derive convergence of the surrogate posterior to the true posterior distribution in the Hellinger metric as our adaptive loss function approaches zero. Furthermore, we describe how this surrogate-accelerated HMC approach can be combined with a traditional PDE solver in a delayed-acceptance scheme to a-priori control the posterior accuracy, thus overcoming a major limitation of deep learning-based surrogate approaches, which do not achieve guaranteed accuracy a-priori due to their non-convex training. Biot number calculations are involved turbo-machinery design, which is safety critical and highly regulated, therefore it is important that our results have such mathematical guarantees. Our approach achieves fast mixing in high-dimensional parameter spaces, whilst retaining the convergence guarantees of a traditional PDE solver, and without the burden of evaluating this solver for proposals that are likely to be rejected. Numerical results compare the accuracy and efficiency of the adaptive and general training regimes, as well as various Markov chain Monte Carlo proposals strategies.

A deep surrogate approach to efficient Bayesian inversion in PDE and integral equation models

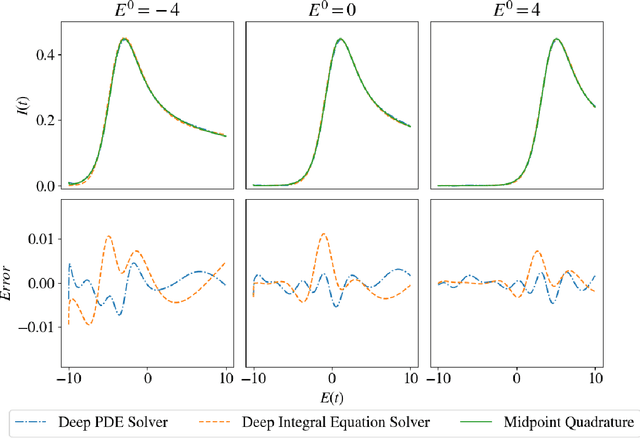
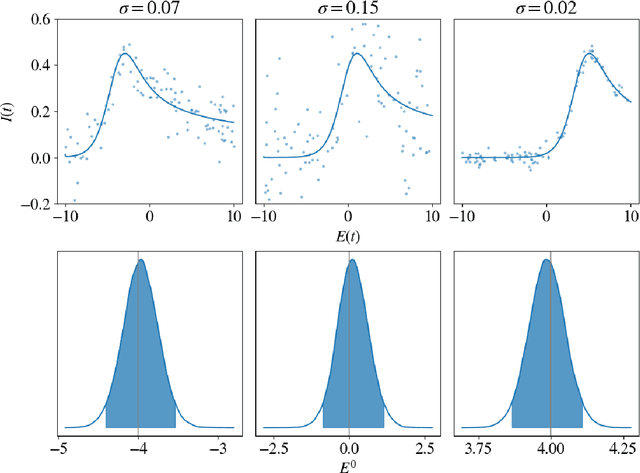
We propose a novel deep learning approach to efficiently perform Bayesian inference in partial differential equation (PDE) and integral equation models over potentially high-dimensional parameter spaces. The contributions of this paper are two-fold; the first is the introduction of a neural network approach to approximating the solutions of Fredholm and Volterra integral equations of the first and second kind. The second is the description of a deep surrogate model which allows for efficient sampling from a Bayesian posterior distribution in which the likelihood depends on the solutions of PDEs or integral equations. For the latter, our method relies on the approximation of parametric solutions by neural networks. This deep learning approach allows for parametric solutions to be approximated accurately in significantly higher dimensions than is possible using classical techniques. These solutions are very cheap to evaluate, making Bayesian inference over large parameter spaces tractable for these models using Markov chain Monte Carlo. We demonstrate this method using two real-world examples; these include Bayesian inference in the PDE and integral equation case for an example from electrochemistry, and Bayesian inference of a function-valued heat-transfer parameter with applications in aviation.