A deep surrogate approach to efficient Bayesian inversion in PDE and integral equation models

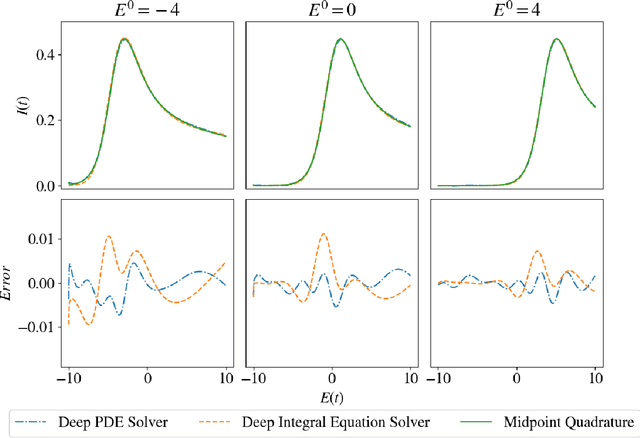
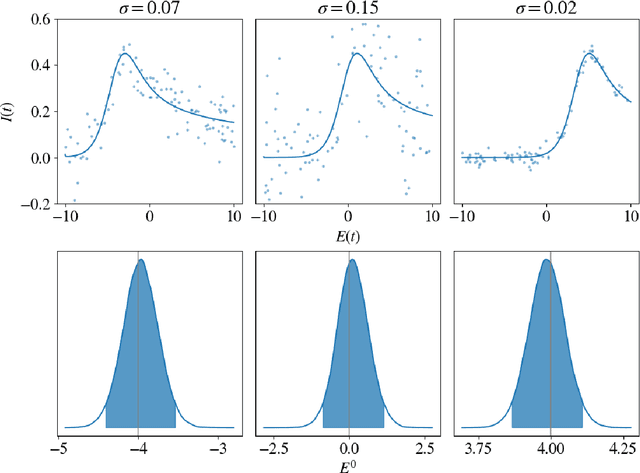
We propose a novel deep learning approach to efficiently perform Bayesian inference in partial differential equation (PDE) and integral equation models over potentially high-dimensional parameter spaces. The contributions of this paper are two-fold; the first is the introduction of a neural network approach to approximating the solutions of Fredholm and Volterra integral equations of the first and second kind. The second is the description of a deep surrogate model which allows for efficient sampling from a Bayesian posterior distribution in which the likelihood depends on the solutions of PDEs or integral equations. For the latter, our method relies on the approximation of parametric solutions by neural networks. This deep learning approach allows for parametric solutions to be approximated accurately in significantly higher dimensions than is possible using classical techniques. These solutions are very cheap to evaluate, making Bayesian inference over large parameter spaces tractable for these models using Markov chain Monte Carlo. We demonstrate this method using two real-world examples; these include Bayesian inference in the PDE and integral equation case for an example from electrochemistry, and Bayesian inference of a function-valued heat-transfer parameter with applications in aviation.