Gaussian Process Diffeomorphic Statistical Shape Modelling Outperforms Angle-Based Methods for Assessment of Hip Dysplasia

Dysplasia is a recognised risk factor for osteoarthritis (OA) of the hip, early diagnosis of dysplasia is important to provide opportunities for surgical interventions aimed at reducing the risk of hip OA. We have developed a pipeline for semi-automated classification of dysplasia using volumetric CT scans of patients' hips and a minimal set of clinically annotated landmarks, combining the framework of the Gaussian Process Latent Variable Model with diffeomorphism to create a statistical shape model, which we termed the Gaussian Process Diffeomorphic Statistical Shape Model (GPDSSM). We used 192 CT scans, 100 for model training and 92 for testing. The GPDSSM effectively distinguishes dysplastic samples from controls while also highlighting regions of the underlying surface that show dysplastic variations. As well as improving classification accuracy compared to angle-based methods (AUC 96.2% vs 91.2%), the GPDSSM can save time for clinicians by removing the need to manually measure angles and interpreting 2D scans for possible markers of dysplasia.

ARC-Flow : Articulated, Resolution-Agnostic, Correspondence-Free Matching and Interpolation of 3D Shapes Under Flow Fields

This work presents a unified framework for the unsupervised prediction of physically plausible interpolations between two 3D articulated shapes and the automatic estimation of dense correspondence between them. Interpolation is modelled as a diffeomorphic transformation using a smooth, time-varying flow field governed by Neural Ordinary Differential Equations (ODEs). This ensures topological consistency and non-intersecting trajectories while accommodating hard constraints, such as volume preservation, and soft constraints, \eg physical priors. Correspondence is recovered using an efficient Varifold formulation, that is effective on high-fidelity surfaces with differing parameterisations. By providing a simple skeleton for the source shape only, we impose physically motivated constraints on the deformation field and resolve symmetric ambiguities. This is achieved without relying on skinning weights or any prior knowledge of the skeleton's target pose configuration. Qualitative and quantitative results demonstrate competitive or superior performance over existing state-of-the-art approaches in both shape correspondence and interpolation tasks across standard datasets.

Compressed online Sinkhorn

The use of optimal transport (OT) distances, and in particular entropic-regularised OT distances, is an increasingly popular evaluation metric in many areas of machine learning and data science. Their use has largely been driven by the availability of efficient algorithms such as the Sinkhorn algorithm. One of the drawbacks of the Sinkhorn algorithm for large-scale data processing is that it is a two-phase method, where one first draws a large stream of data from the probability distributions, before applying the Sinkhorn algorithm to the discrete probability measures. More recently, there have been several works developing stochastic versions of Sinkhorn that directly handle continuous streams of data. In this work, we revisit the recently introduced online Sinkhorn algorithm of [Mensch and Peyr\'e, 2020]. Our contributions are twofold: We improve the convergence analysis for the online Sinkhorn algorithm, the new rate that we obtain is faster than the previous rate under certain parameter choices. We also present numerical results to verify the sharpness of our result. Secondly, we propose the compressed online Sinkhorn algorithm which combines measure compression techniques with the online Sinkhorn algorithm. We provide numerical experiments to show practical numerical gains, as well as theoretical guarantees on the efficiency of our approach.

Deep surrogate accelerated delayed-acceptance HMC for Bayesian inference of spatio-temporal heat fluxes in rotating disc systems

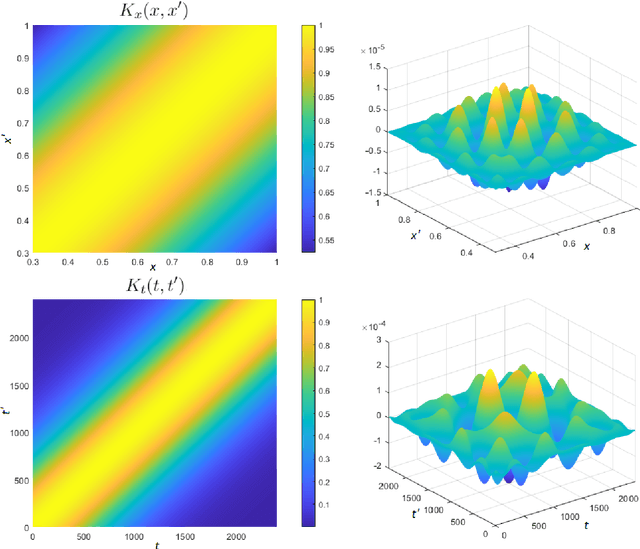
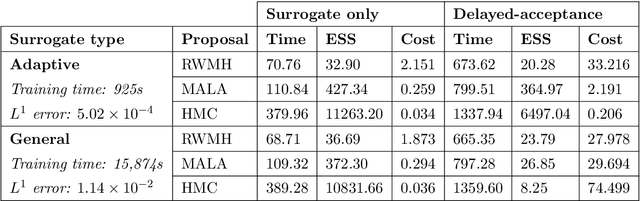
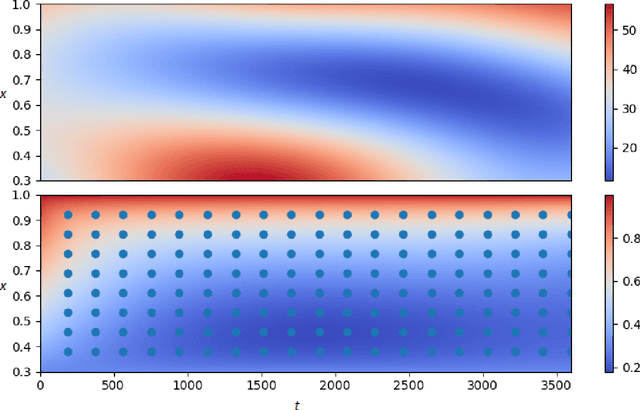
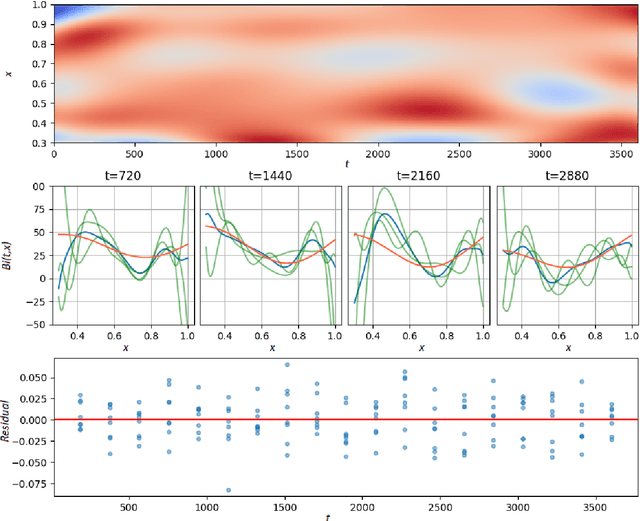
We study the Bayesian inverse problem of inferring the Biot number, a spatio-temporal heat-flux parameter in a PDE model. This is an ill-posed problem where standard optimisation yields unphysical inferences. We introduce a training scheme that uses temperature data to adaptively train a neural-network surrogate to simulate the parametric forward model. This approach approximates forward and inverse solution together, by simultaneously identifying an approximate posterior distribution over the Biot number, and weighting the forward training loss according to this approximation. Utilising random Chebyshev series, we outline how to approximate an arbitrary Gaussian process prior, and using the surrogate we apply Hamiltonian Monte Carlo (HMC) to efficiently sample from the corresponding posterior distribution. We derive convergence of the surrogate posterior to the true posterior distribution in the Hellinger metric as our adaptive loss function approaches zero. Furthermore, we describe how this surrogate-accelerated HMC approach can be combined with a traditional PDE solver in a delayed-acceptance scheme to a-priori control the posterior accuracy, thus overcoming a major limitation of deep learning-based surrogate approaches, which do not achieve guaranteed accuracy a-priori due to their non-convex training. Biot number calculations are involved turbo-machinery design, which is safety critical and highly regulated, therefore it is important that our results have such mathematical guarantees. Our approach achieves fast mixing in high-dimensional parameter spaces, whilst retaining the convergence guarantees of a traditional PDE solver, and without the burden of evaluating this solver for proposals that are likely to be rejected. Numerical results compare the accuracy and efficiency of the adaptive and general training regimes, as well as various Markov chain Monte Carlo proposals strategies.

A deep surrogate approach to efficient Bayesian inversion in PDE and integral equation models

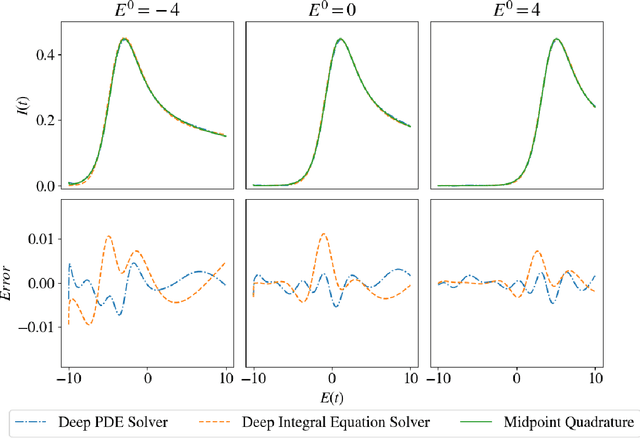
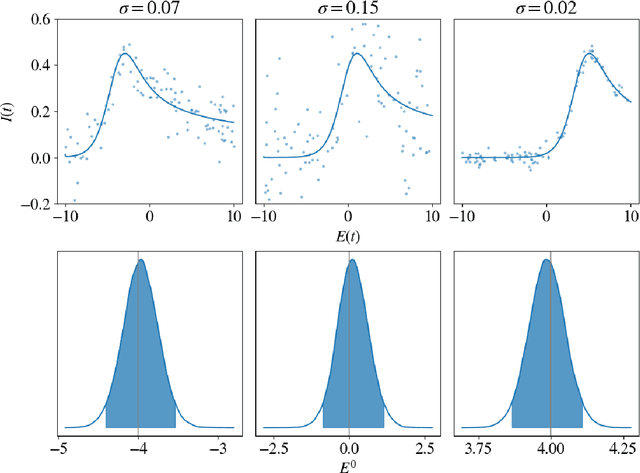
We propose a novel deep learning approach to efficiently perform Bayesian inference in partial differential equation (PDE) and integral equation models over potentially high-dimensional parameter spaces. The contributions of this paper are two-fold; the first is the introduction of a neural network approach to approximating the solutions of Fredholm and Volterra integral equations of the first and second kind. The second is the description of a deep surrogate model which allows for efficient sampling from a Bayesian posterior distribution in which the likelihood depends on the solutions of PDEs or integral equations. For the latter, our method relies on the approximation of parametric solutions by neural networks. This deep learning approach allows for parametric solutions to be approximated accurately in significantly higher dimensions than is possible using classical techniques. These solutions are very cheap to evaluate, making Bayesian inference over large parameter spaces tractable for these models using Markov chain Monte Carlo. We demonstrate this method using two real-world examples; these include Bayesian inference in the PDE and integral equation case for an example from electrochemistry, and Bayesian inference of a function-valued heat-transfer parameter with applications in aviation.