Compressed online Sinkhorn

The use of optimal transport (OT) distances, and in particular entropic-regularised OT distances, is an increasingly popular evaluation metric in many areas of machine learning and data science. Their use has largely been driven by the availability of efficient algorithms such as the Sinkhorn algorithm. One of the drawbacks of the Sinkhorn algorithm for large-scale data processing is that it is a two-phase method, where one first draws a large stream of data from the probability distributions, before applying the Sinkhorn algorithm to the discrete probability measures. More recently, there have been several works developing stochastic versions of Sinkhorn that directly handle continuous streams of data. In this work, we revisit the recently introduced online Sinkhorn algorithm of [Mensch and Peyr\'e, 2020]. Our contributions are twofold: We improve the convergence analysis for the online Sinkhorn algorithm, the new rate that we obtain is faster than the previous rate under certain parameter choices. We also present numerical results to verify the sharpness of our result. Secondly, we propose the compressed online Sinkhorn algorithm which combines measure compression techniques with the online Sinkhorn algorithm. We provide numerical experiments to show practical numerical gains, as well as theoretical guarantees on the efficiency of our approach.

Smooth over-parameterized solvers for non-smooth structured optimization

Non-smooth optimization is a core ingredient of many imaging or machine learning pipelines. Non-smoothness encodes structural constraints on the solutions, such as sparsity, group sparsity, low-rank and sharp edges. It is also the basis for the definition of robust loss functions and scale-free functionals such as square-root Lasso. Standard approaches to deal with non-smoothness leverage either proximal splitting or coordinate descent. These approaches are effective but usually require parameter tuning, preconditioning or some sort of support pruning. In this work, we advocate and study a different route, which operates a non-convex but smooth over-parametrization of the underlying non-smooth optimization problems. This generalizes quadratic variational forms that are at the heart of the popular Iterative Reweighted Least Squares (IRLS). Our main theoretical contribution connects gradient descent on this reformulation to a mirror descent flow with a varying Hessian metric. This analysis is crucial to derive convergence bounds that are dimension-free. This explains the efficiency of the method when using small grid sizes in imaging. Our main algorithmic contribution is to apply the Variable Projection (VarPro) method which defines a new formulation by explicitly minimizing over part of the variables. This leads to a better conditioning of the minimized functional and improves the convergence of simple but very efficient gradient-based methods, for instance quasi-Newton solvers. We exemplify the use of this new solver for the resolution of regularized regression problems for inverse problems and supervised learning, including total variation prior and non-convex regularizers.

Smooth Bilevel Programming for Sparse Regularization

Iteratively reweighted least square (IRLS) is a popular approach to solve sparsity-enforcing regression problems in machine learning. State of the art approaches are more efficient but typically rely on specific coordinate pruning schemes. In this work, we show how a surprisingly simple reparametrization of IRLS, coupled with a bilevel resolution (instead of an alternating scheme) is able to achieve top performances on a wide range of sparsity (such as Lasso, group Lasso and trace norm regularizations), regularization strength (including hard constraints), and design matrices (ranging from correlated designs to differential operators). Similarly to IRLS, our method only involves linear systems resolutions, but in sharp contrast, corresponds to the minimization of a smooth function. Despite being non-convex, we show that there is no spurious minima and that saddle points are "ridable", so that there always exists a descent direction. We thus advocate for the use of a BFGS quasi-Newton solver, which makes our approach simple, robust and efficient. We perform a numerical benchmark of the convergence speed of our algorithm against state of the art solvers for Lasso, group Lasso, trace norm and linearly constrained problems. These results highlight the versatility of our approach, removing the need to use different solvers depending on the specificity of the ML problem under study.

Screening for Sparse Online Learning

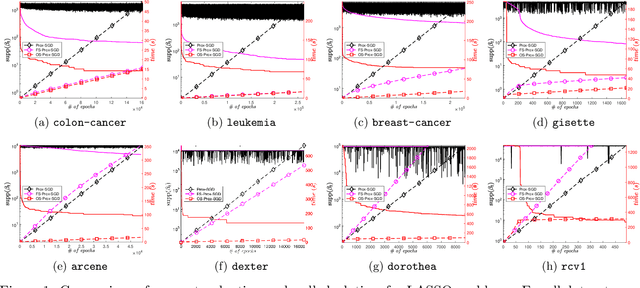
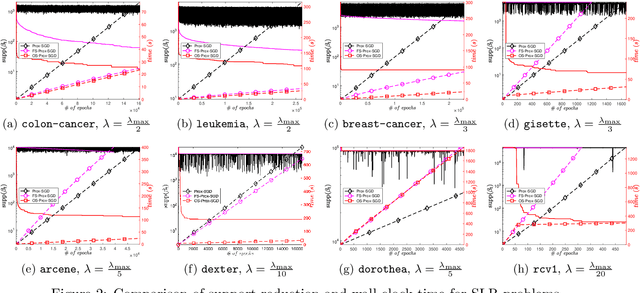
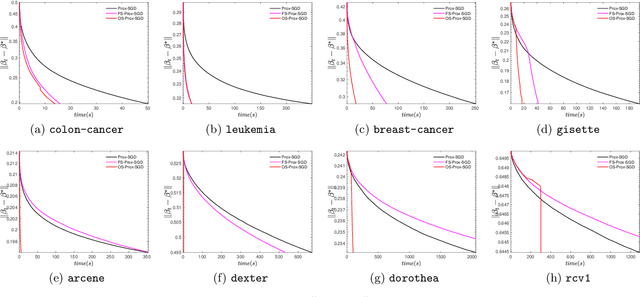
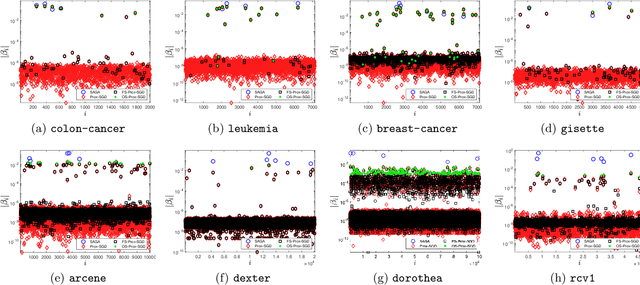
Sparsity promoting regularizers are widely used to impose low-complexity structure (e.g. l1-norm for sparsity) to the regression coefficients of supervised learning. In the realm of deterministic optimization, the sequence generated by iterative algorithms (such as proximal gradient descent) exhibit "finite activity identification", namely, they can identify the low-complexity structure in a finite number of iterations. However, most online algorithms (such as proximal stochastic gradient descent) do not have the property owing to the vanishing step-size and non-vanishing variance. In this paper, by combining with a screening rule, we show how to eliminate useless features of the iterates generated by online algorithms, and thereby enforce finite activity identification. One consequence is that when combined with any convergent online algorithm, sparsity properties imposed by the regularizer can be exploited for computational gains. Numerically, significant acceleration can be obtained.

An off-the-grid approach to multi-compartment magnetic resonance fingerprinting

We propose a novel numerical approach to separate multiple tissue compartments in image voxels and to estimate quantitatively their nuclear magnetic resonance (NMR) properties and mixture fractions, given magnetic resonance fingerprinting (MRF) measurements. The number of tissues, their types or quantitative properties are not a-priori known, but the image is assumed to be composed of sparse compartments with linearly mixed Bloch magnetisation responses within voxels. Fine-grid discretisation of the multi-dimensional NMR properties creates large and highly coherent MRF dictionaries that can challenge scalability and precision of the numerical methods for (discrete) sparse approximation. To overcome these issues, we propose an off-the-grid approach equipped with an extended notion of the sparse group lasso regularisation for sparse approximation using continuous (non-discretised) Bloch response models. Further, the nonlinear and non-analytical Bloch responses are approximated by a neural network, enabling efficient back-propagation of the gradients through the proposed algorithm. Tested on simulated and in-vivo healthy brain MRF data, we demonstrate effectiveness of the proposed scheme compared to the baseline multicompartment MRF methods.

Degrees of freedom for off-the-grid sparse estimation

A central question in modern machine learning and imaging sciences is to quantify the number of effective parameters of vastly over-parameterized models. The degrees of freedom is a mathematically convenient way to define this number of parameters. Its computation and properties are well understood when dealing with discretized linear models, possibly regularized using sparsity. In this paper, we argue that this way of thinking is plagued when dealing with models having very large parameter spaces. In this case it makes more sense to consider "off-the-grid" approaches, using a continuous parameter space. This type of approach is the one favoured when training multi-layer perceptrons, and is also becoming popular to solve super-resolution problems in imaging. Training these off-the-grid models with a sparsity inducing prior can be achieved by solving a convex optimization problem over the space of measures, which is often called the Beurling Lasso (Blasso), and is the continuous counterpart of the celebrated Lasso parameter selection method. In previous works, the degrees of freedom for the Lasso was shown to coincide with the size of the smallest solution support. Our main contribution is a proof of a continuous counterpart to this result for the Blasso. Our findings suggest that discretized methods actually vastly over-estimate the number of intrinsic continuous degrees of freedom. Our second contribution is a detailed study of the case of sampling Fourier coefficients in 1D, which corresponds to a super-resolution problem. We show that our formula for the degrees of freedom is valid outside of a set of measure zero of observations, which in turn justifies its use to compute an unbiased estimator of the prediction risk using the Stein Unbiased Risk Estimator (SURE).

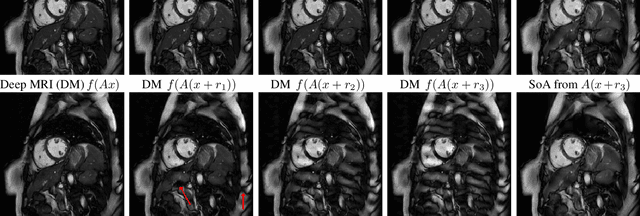
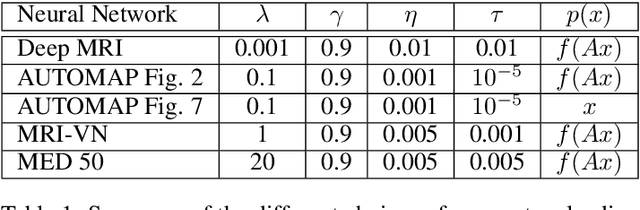
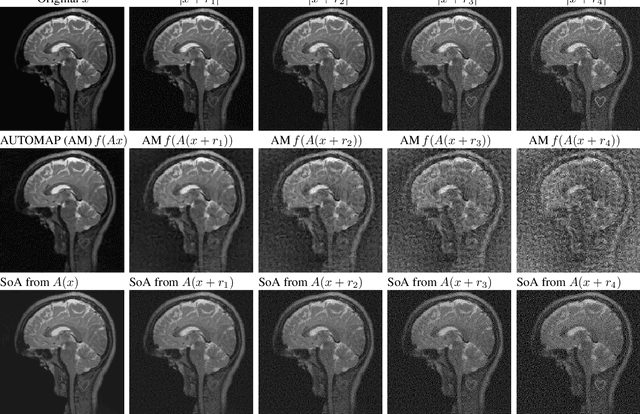
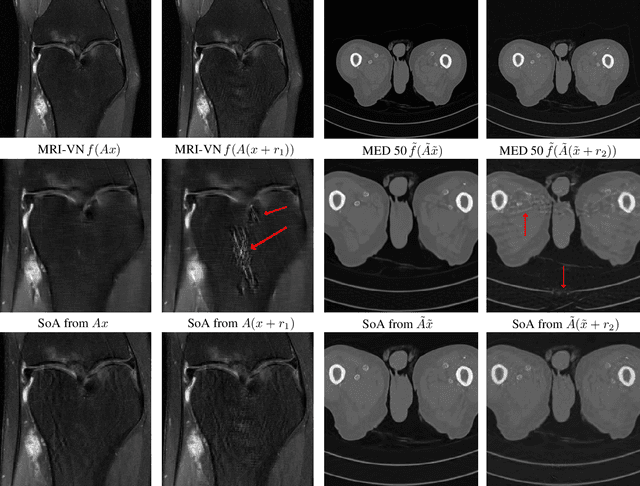
On instabilities of deep learning in image reconstruction - Does AI come at a cost?

Deep learning, due to its unprecedented success in tasks such as image classification, has emerged as a new tool in image reconstruction with potential to change the field. In this paper we demonstrate a crucial phenomenon: deep learning typically yields unstablemethods for image reconstruction. The instabilities usually occur in several forms: (1) tiny, almost undetectable perturbations, both in the image and sampling domain, may result in severe artefacts in the reconstruction, (2) a small structural change, for example a tumour, may not be captured in the reconstructed image and (3) (a counterintuitive type of instability) more samples may yield poorer performance. Our new stability test with algorithms and easy to use software detects the instability phenomena. The test is aimed at researchers to test their networks for instabilities and for government agencies, such as the Food and Drug Administration (FDA), to secure safe use of deep learning methods.