Instance-wise Uncertainty for Class Imbalance in Semantic Segmentation

Semantic segmentation is a fundamental computer vision task with a vast number of applications. State of the art methods increasingly rely on deep learning models, known to incorrectly estimate uncertainty and being overconfident in predictions, especially in data not seen during training. This is particularly problematic in semantic segmentation due to inherent class imbalance. Popular uncertainty quantification approaches are task-agnostic and fail to leverage spatial pixel correlations in uncertainty estimates, crucial in this task. In this work, a novel training methodology specifically designed for semantic segmentation is presented. Training samples are weighted by instance-wise uncertainty masks computed by an ensemble. This is shown to increase performance on minority classes, boost model generalization and robustness to domain-shift when compared to using the inverse of class proportions or no class weights at all. This method addresses the challenges of class imbalance and uncertainty estimation in semantic segmentation, potentially enhancing model performance and reliability across various applications.

Beyond Heart Murmur Detection: Automatic Murmur Grading from Phonocardiogram

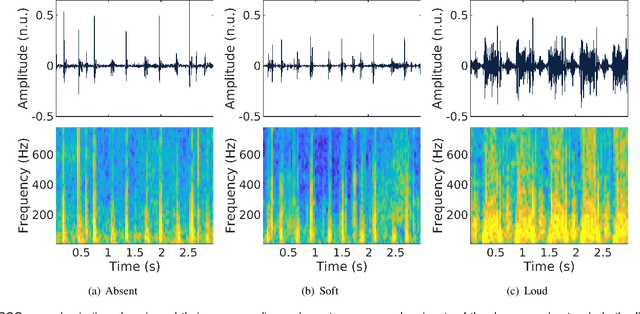
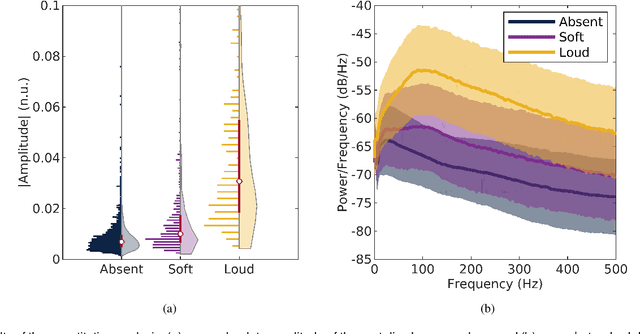
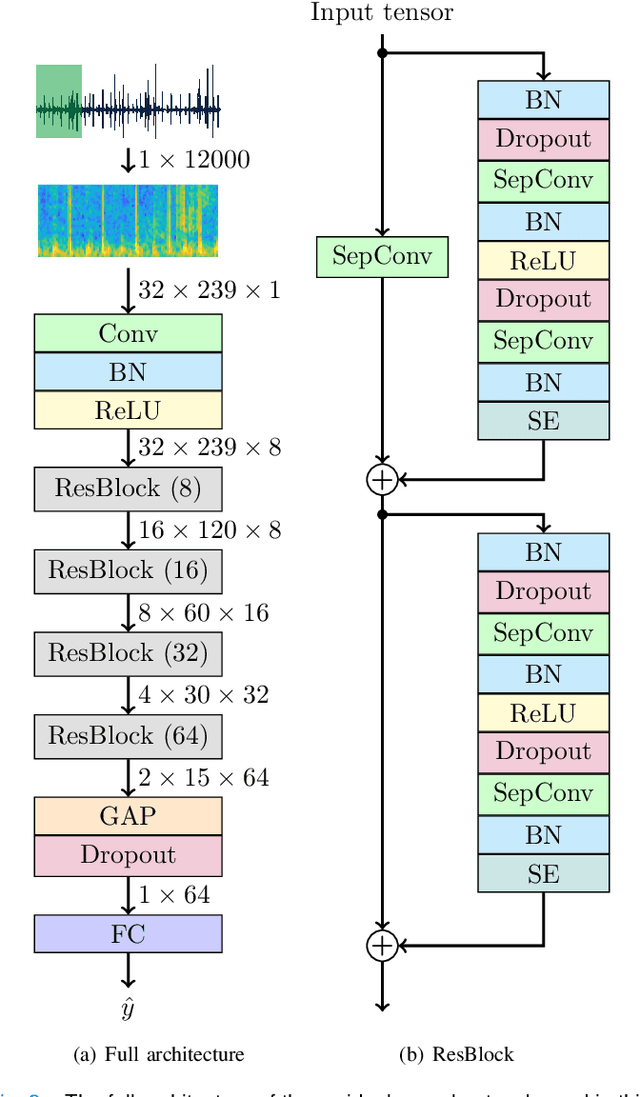
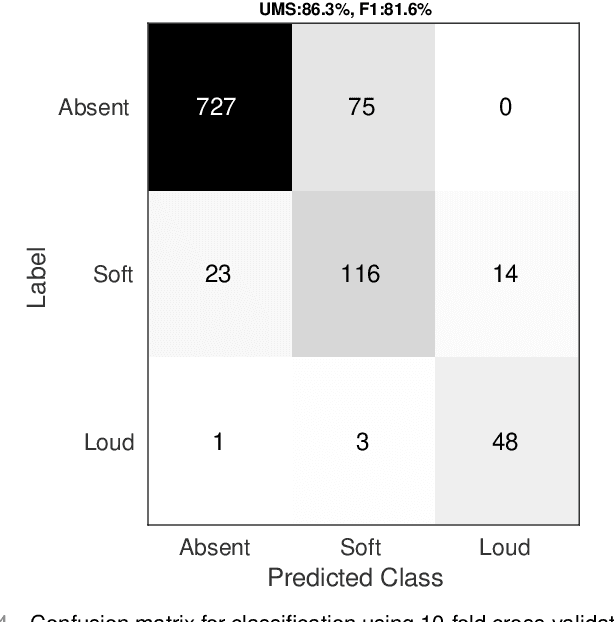
Objective: Murmurs are abnormal heart sounds, identified by experts through cardiac auscultation. The murmur grade, a quantitative measure of the murmur intensity, is strongly correlated with the patient's clinical condition. This work aims to estimate each patient's murmur grade (i.e., absent, soft, loud) from multiple auscultation location phonocardiograms (PCGs) of a large population of pediatric patients from a low-resource rural area. Methods: The Mel spectrogram representation of each PCG recording is given to an ensemble of 15 convolutional residual neural networks with channel-wise attention mechanisms to classify each PCG recording. The final murmur grade for each patient is derived based on the proposed decision rule and considering all estimated labels for available recordings. The proposed method is cross-validated on a dataset consisting of 3456 PCG recordings from 1007 patients using a stratified ten-fold cross-validation. Additionally, the method was tested on a hidden test set comprised of 1538 PCG recordings from 442 patients. Results: The overall cross-validation performances for patient-level murmur gradings are 86.3% and 81.6% in terms of the unweighted average of sensitivities and F1-scores, respectively. The sensitivities (and F1-scores) for absent, soft, and loud murmurs are 90.7% (93.6%), 75.8% (66.8%), and 92.3% (84.2%), respectively. On the test set, the algorithm achieves an unweighted average of sensitivities of 80.4% and an F1-score of 75.8%. Conclusions: This study provides a potential approach for algorithmic pre-screening in low-resource settings with relatively high expert screening costs. Significance: The proposed method represents a significant step beyond detection of murmurs, providing characterization of intensity which may provide a enhanced classification of clinical outcomes.

The CirCor DigiScope Dataset: From Murmur Detection to Murmur Classification

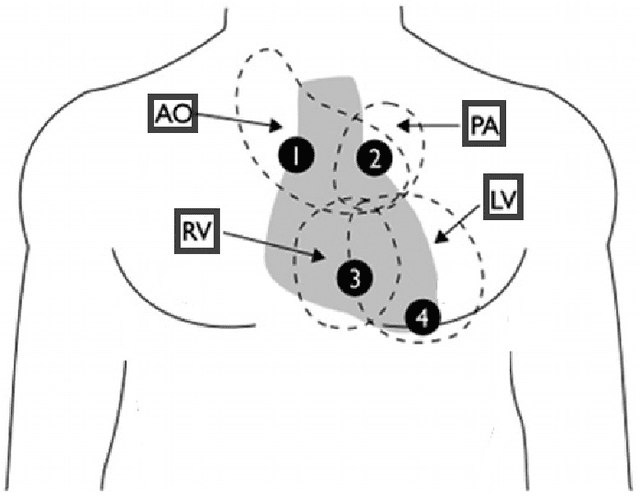
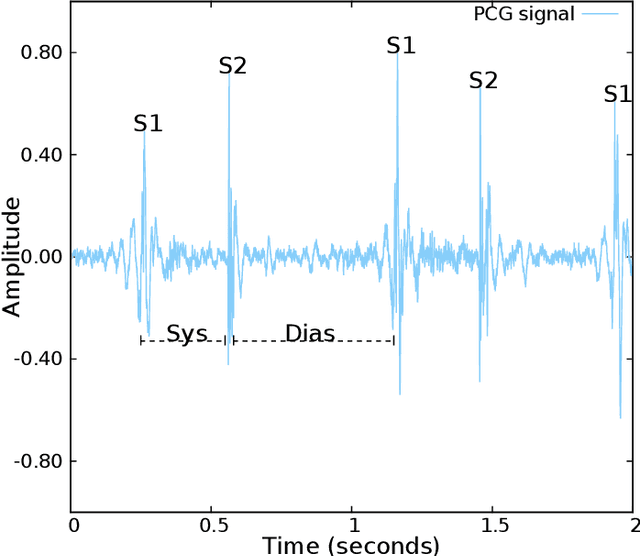
Cardiac auscultation is one of the most cost-effective techniques used to detect and identify many heart conditions. Computer-assisted decision systems based on auscultation can support physicians in their decisions. Unfortunately, the application of such systems in clinical trials is still minimal since most of them only aim to detect the presence of extra or abnormal waves in the phonocardiogram signal. This is mainly due to the lack of large publicly available datasets, where a more detailed description of such abnormal waves (e.g., cardiac murmurs) exists. As a result, current machine learning algorithms are unable to classify such waves. To pave the way to more effective research on healthcare recommendation systems based on auscultation, our team has prepared the currently largest pediatric heart sound dataset. A total of 5282 recordings have been collected from the four main auscultation locations of 1568 patients, in the process 215780 heart sounds have been manually annotated. Furthermore, and for the first time, each cardiac murmur has been manually annotated by an expert annotator according to its timing, shape, pitch, grading and quality. In addition, the auscultation locations where the murmur is present were identified as well as the auscultation location where the murmur is detected more intensively.

On instabilities of deep learning in image reconstruction - Does AI come at a cost?

Deep learning, due to its unprecedented success in tasks such as image classification, has emerged as a new tool in image reconstruction with potential to change the field. In this paper we demonstrate a crucial phenomenon: deep learning typically yields unstablemethods for image reconstruction. The instabilities usually occur in several forms: (1) tiny, almost undetectable perturbations, both in the image and sampling domain, may result in severe artefacts in the reconstruction, (2) a small structural change, for example a tumour, may not be captured in the reconstructed image and (3) (a counterintuitive type of instability) more samples may yield poorer performance. Our new stability test with algorithms and easy to use software detects the instability phenomena. The test is aimed at researchers to test their networks for instabilities and for government agencies, such as the Food and Drug Administration (FDA), to secure safe use of deep learning methods.

Bounds on the Number of Measurements for Reliable Compressive Classification

This paper studies the classification of high-dimensional Gaussian signals from low-dimensional noisy, linear measurements. In particular, it provides upper bounds (sufficient conditions) on the number of measurements required to drive the probability of misclassification to zero in the low-noise regime, both for random measurements and designed ones. Such bounds reveal two important operational regimes that are a function of the characteristics of the source: i) when the number of classes is less than or equal to the dimension of the space spanned by signals in each class, reliable classification is possible in the low-noise regime by using a one-vs-all measurement design; ii) when the dimension of the spaces spanned by signals in each class is lower than the number of classes, reliable classification is guaranteed in the low-noise regime by using a simple random measurement design. Simulation results both with synthetic and real data show that our analysis is sharp, in the sense that it is able to gauge the number of measurements required to drive the misclassification probability to zero in the low-noise regime.

Classification and Reconstruction of High-Dimensional Signals from Low-Dimensional Features in the Presence of Side Information

This paper offers a characterization of fundamental limits on the classification and reconstruction of high-dimensional signals from low-dimensional features, in the presence of side information. We consider a scenario where a decoder has access both to linear features of the signal of interest and to linear features of the side information signal; while the side information may be in a compressed form, the objective is recovery or classification of the primary signal, not the side information. The signal of interest and the side information are each assumed to have (distinct) latent discrete labels; conditioned on these two labels, the signal of interest and side information are drawn from a multivariate Gaussian distribution. With joint probabilities on the latent labels, the overall signal-(side information) representation is defined by a Gaussian mixture model. We then provide sharp sufficient and/or necessary conditions for these quantities to approach zero when the covariance matrices of the Gaussians are nearly low-rank. These conditions, which are reminiscent of the well-known Slepian-Wolf and Wyner-Ziv conditions, are a function of the number of linear features extracted from the signal of interest, the number of linear features extracted from the side information signal, and the geometry of these signals and their interplay. Moreover, on assuming that the signal of interest and the side information obey such an approximately low-rank model, we derive expansions of the reconstruction error as a function of the deviation from an exactly low-rank model; such expansions also allow identification of operational regimes where the impact of side information on signal reconstruction is most relevant. Our framework, which offers a principled mechanism to integrate side information in high-dimensional data problems, is also tested in the context of imaging applications.

Mismatch in the Classification of Linear Subspaces: Sufficient Conditions for Reliable Classification

This paper considers the classification of linear subspaces with mismatched classifiers. In particular, we assume a model where one observes signals in the presence of isotropic Gaussian noise and the distribution of the signals conditioned on a given class is Gaussian with a zero mean and a low-rank covariance matrix. We also assume that the classifier knows only a mismatched version of the parameters of input distribution in lieu of the true parameters. By constructing an asymptotic low-noise expansion of an upper bound to the error probability of such a mismatched classifier, we provide sufficient conditions for reliable classification in the low-noise regime that are able to sharply predict the absence of a classification error floor. Such conditions are a function of the geometry of the true signal distribution, the geometry of the mismatched signal distributions as well as the interplay between such geometries, namely, the principal angles and the overlap between the true and the mismatched signal subspaces. Numerical results demonstrate that our conditions for reliable classification can sharply predict the behavior of a mismatched classifier both with synthetic data and in a motion segmentation and a hand-written digit classification applications.