Galen Reeves
What happens when generative AI models train recursively on each others' generated outputs?
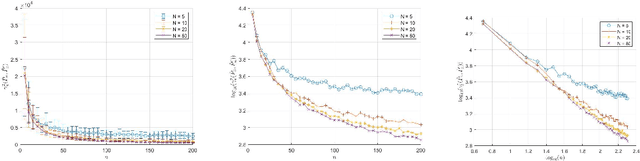
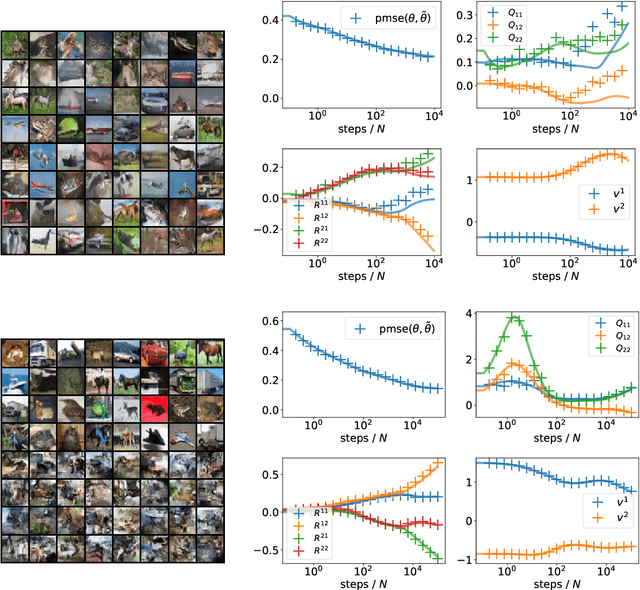
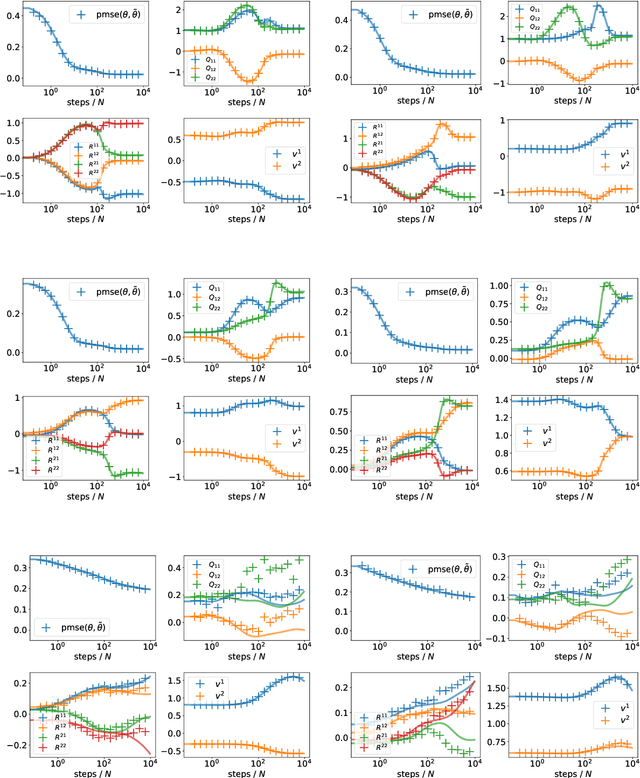
May 27, 2025Abstract:The internet is full of AI-generated content while also serving as a common source of training data for generative AI (genAI) models. This duality raises the possibility that future genAI models may be trained on other models' generated outputs. Prior work has studied consequences of models training on their own generated outputs, but limited work has considered what happens if models ingest content produced by other models. Given society's increasing dependence on genAI tools, understanding downstream effects of such data-mediated model interactions is critical. To this end, we provide empirical evidence for how data-mediated interactions might unfold in practice, develop a theoretical model for this interactive training process, and show experimentally possible long-term results of such interactions. We find that data-mediated interactions can benefit models by exposing them to novel concepts perhaps missed in original training data, but also can homogenize their performance on shared tasks.
Information-Theoretic Proofs for Diffusion Sampling
Feb 04, 2025Abstract:This paper provides an elementary, self-contained analysis of diffusion-based sampling methods for generative modeling. In contrast to existing approaches that rely on continuous-time processes and then discretize, our treatment works directly with discrete-time stochastic processes and yields precise non-asymptotic convergence guarantees under broad assumptions. The key insight is to couple the sampling process of interest with an idealized comparison process that has an explicit Gaussian-convolution structure. We then leverage simple identities from information theory, including the I-MMSE relationship, to bound the discrepancy (in terms of the Kullback-Leibler divergence) between these two discrete-time processes. In particular, we show that, if the diffusion step sizes are chosen sufficiently small and one can approximate certain conditional mean estimators well, then the sampling distribution is provably close to the target distribution. Our results also provide a transparent view on how to accelerate convergence by introducing additional randomness in each step to match higher order moments in the comparison process.
Approximate Message Passing for the Matrix Tensor Product Model
Jun 27, 2023Abstract:We propose and analyze an approximate message passing (AMP) algorithm for the matrix tensor product model, which is a generalization of the standard spiked matrix models that allows for multiple types of pairwise observations over a collection of latent variables. A key innovation for this algorithm is a method for optimally weighing and combining multiple estimates in each iteration. Building upon an AMP convergence theorem for non-separable functions, we prove a state evolution for non-separable functions that provides an asymptotically exact description of its performance in the high-dimensional limit. We leverage this state evolution result to provide necessary and sufficient conditions for recovery of the signal of interest. Such conditions depend on the singular values of a linear operator derived from an appropriate generalization of a signal-to-noise ratio for our model. Our results recover as special cases a number of recently proposed methods for contextual models (e.g., covariate assisted clustering) as well as inhomogeneous noise models.
k-Sliced Mutual Information: A Quantitative Study of Scalability with Dimension
Jun 17, 2022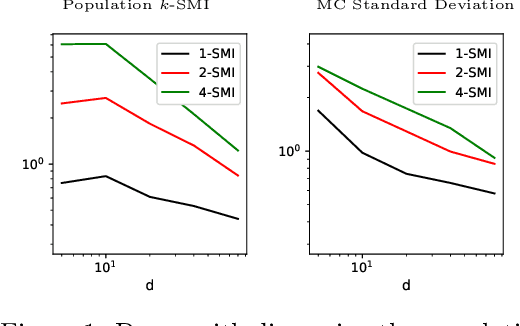

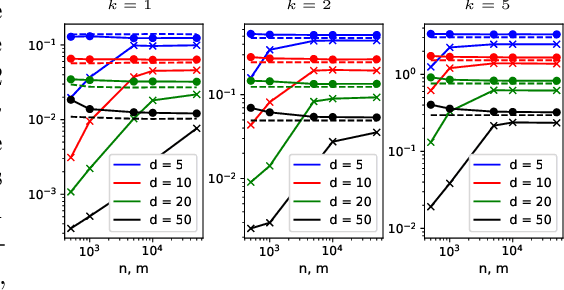

Abstract:Sliced mutual information (SMI) is defined as an average of mutual information (MI) terms between one-dimensional random projections of the random variables. It serves as a surrogate measure of dependence to classic MI that preserves many of its properties but is more scalable to high dimensions. However, a quantitative characterization of how SMI itself and estimation rates thereof depend on the ambient dimension, which is crucial to the understanding of scalability, remain obscure. This works extends the original SMI definition to $k$-SMI, which considers projections to $k$-dimensional subspaces, and provides a multifaceted account on its dependence on dimension. Using a new result on the continuity of differential entropy in the 2-Wasserstein metric, we derive sharp bounds on the error of Monte Carlo (MC)-based estimates of $k$-SMI, with explicit dependence on $k$ and the ambient dimension, revealing their interplay with the number of samples. We then combine the MC integrator with the neural estimation framework to provide an end-to-end $k$-SMI estimator, for which optimal convergence rates are established. We also explore asymptotics of the population $k$-SMI as dimension grows, providing Gaussian approximation results with a residual that decays under appropriate moment bounds. Our theory is validated with numerical experiments and is applied to sliced InfoGAN, which altogether provide a comprehensive quantitative account of the scalability question of $k$-SMI, including SMI as a special case when $k=1$.
Rank-one matrix estimation with groupwise heteroskedasticity
Jun 22, 2021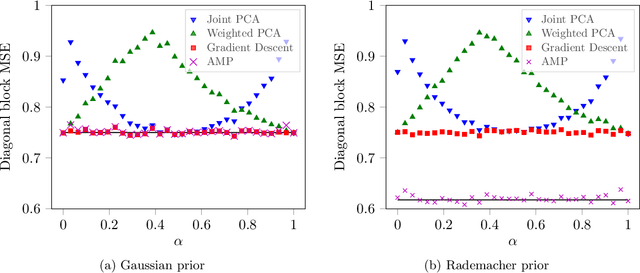
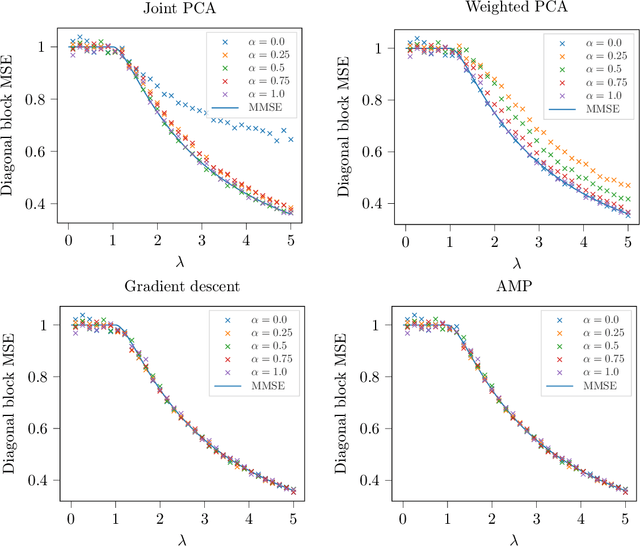
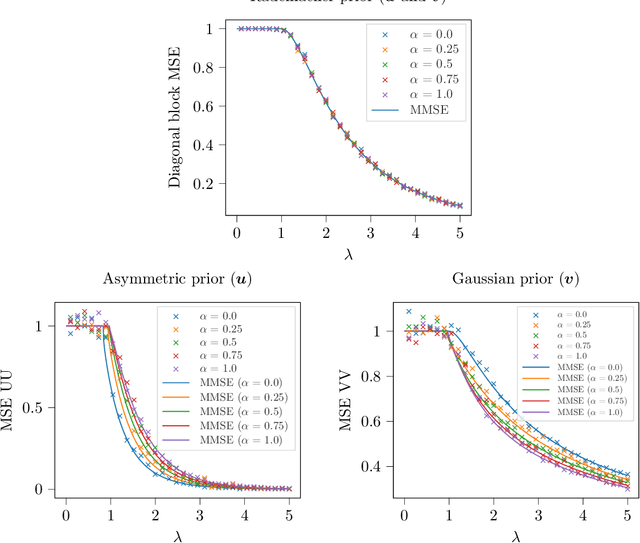
Abstract:We study the problem of estimating a rank-one matrix from Gaussian observations where different blocks of the matrix are observed under different noise levels. This problem is motivated by applications in clustering and community detection where latent variables can be partitioned into a fixed number of known groups (e.g., users and items) and the blocks of the matrix correspond to different types of pairwise interactions (e.g., user-user, user-item, or item-item interactions). In the setting where the number of blocks is fixed while the number of variables tends to infinity, we prove asymptotically exact formulas for the minimum mean-squared error in estimating both the matrix and the latent variables. These formulas describe the weak recovery thresholds for the problem and reveal invariance properties with respect to certain scalings of the noise variance. We also derive an approximate message passing algorithm and a gradient descent algorithm and show empirically that these algorithms achieve the information-theoretic limits in certain regimes.
Convergence of Gaussian-smoothed optimal transport distance with sub-gamma distributions and dependent samples
Feb 28, 2021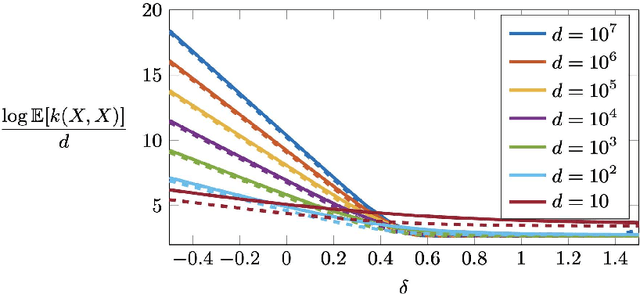
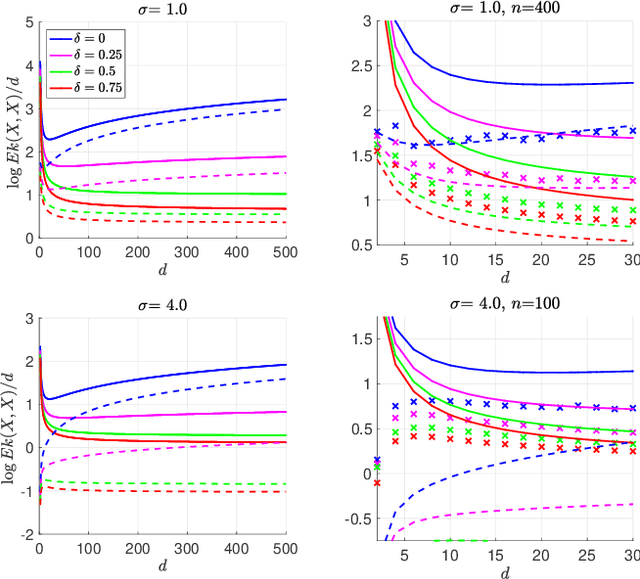
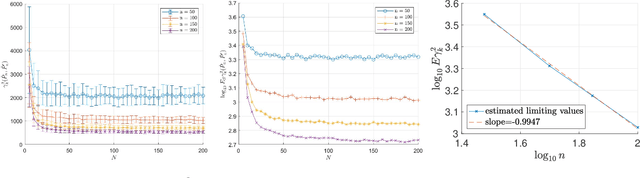
Abstract:The Gaussian-smoothed optimal transport (GOT) framework, recently proposed by Goldfeld et al., scales to high dimensions in estimation and provides an alternative to entropy regularization. This paper provides convergence guarantees for estimating the GOT distance under more general settings. For the Gaussian-smoothed $p$-Wasserstein distance in $d$ dimensions, our results require only the existence of a moment greater than $d + 2p$. For the special case of sub-gamma distributions, we quantify the dependence on the dimension $d$ and establish a phase transition with respect to the scale parameter. We also prove convergence for dependent samples, only requiring a condition on the pairwise dependence of the samples measured by the covariance of the feature map of a kernel space. A key step in our analysis is to show that the GOT distance is dominated by a family of kernel maximum mean discrepancy (MMD) distances with a kernel that depends on the cost function as well as the amount of Gaussian smoothing. This insight provides further interpretability for the GOT framework and also introduces a class of kernel MMD distances with desirable properties. The theoretical results are supported by numerical experiments.
The Gaussian equivalence of generative models for learning with two-layer neural networks
Jun 25, 2020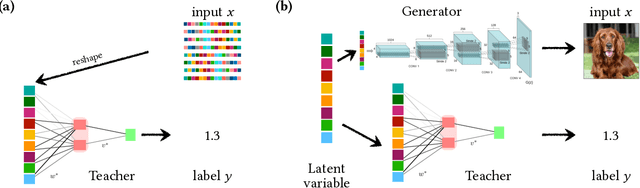

Abstract:Understanding the impact of data structure on learning in neural networks remains a key challenge for the theory of neural networks. Many theoretical works on neural networks do not explicitly model training data, or assume that inputs are drawn independently from some factorised probability distribution. Here, we go beyond the simple i.i.d. modelling paradigm by studying neural networks trained on data drawn from structured generative models. We make three contributions: First, we establish rigorous conditions under which a class of generative models shares key statistical properties with an appropriately chosen Gaussian feature model. Second, we use this Gaussian equivalence theorem (GET) to derive a closed set of equations that describe the dynamics of two-layer neural networks trained using one-pass stochastic gradient descent on data drawn from a large class of generators. We complement our theoretical results by experiments demonstrating how our theory applies to deep, pre-trained generative models.
Information-Theoretic Limits for the Matrix Tensor Product
May 22, 2020Abstract:This paper studies a high-dimensional inference problem involving the matrix tensor product of random matrices. This problem generalizes a number of contemporary data science problems including the spiked matrix models used in sparse principal component analysis and covariance estimation. It is shown that the information-theoretic limits can be described succinctly by formulas involving low-dimensional quantities. On the technical side, this paper introduces some new techniques for the analysis of high-dimensional matrix-valued signals. Specific contributions include a novel extension of the adaptive interpolation method that uses order-preserving positive semidefinite interpolation paths and a variance inequality based on continuous-time I-MMSE relations.
Information-theoretic limits of a multiview low-rank symmetric spiked matrix model
May 16, 2020Abstract:We consider a generalization of an important class of high-dimensional inference problems, namely spiked symmetric matrix models, often used as probabilistic models for principal component analysis. Such paradigmatic models have recently attracted a lot of attention from a number of communities due to their phenomenological richness with statistical-to-computational gaps, while remaining tractable. We rigorously establish the information-theoretic limits through the proof of single-letter formulas for the mutual information and minimum mean-square error. On a technical side we improve the recently introduced adaptive interpolation method, so that it can be used to study low-rank models (i.e., estimation problems of "tall matrices") in full generality, an important step towards the rigorous analysis of more complicated inference and learning models.
Gaussian Approximation of Quantization Error for Estimation from Compressed Data
Jan 09, 2020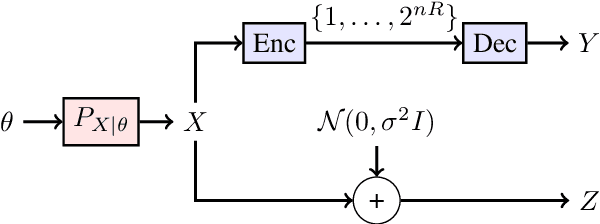


Abstract:We consider the distributional connection between the lossy compressed representation of a high-dimensional signal $X$ using a random spherical code and the observation of $X$ under an additive white Gaussian noise (AWGN). We show that the Wasserstein distance between a bitrate-$R$ compressed version of $X$ and its observation under an AWGN-channel of signal-to-noise ratio $2^{2R}-1$ is sub-linear in the problem dimension. We utilize this fact to connect the risk of an estimator based on an AWGN-corrupted version of $X$ to the risk attained by the same estimator when fed with its bitrate-$R$ quantized version. We demonstrate the usefulness of this connection by deriving various novel results for inference problems under compression constraints, including noisy source coding and limited-bitrate parameter estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge