Gaussian Approximation of Quantization Error for Estimation from Compressed Data
Paper and Code
Jan 09, 2020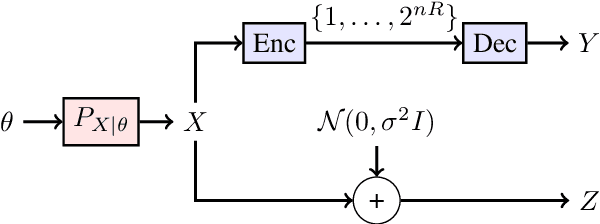


We consider the distributional connection between the lossy compressed representation of a high-dimensional signal $X$ using a random spherical code and the observation of $X$ under an additive white Gaussian noise (AWGN). We show that the Wasserstein distance between a bitrate-$R$ compressed version of $X$ and its observation under an AWGN-channel of signal-to-noise ratio $2^{2R}-1$ is sub-linear in the problem dimension. We utilize this fact to connect the risk of an estimator based on an AWGN-corrupted version of $X$ to the risk attained by the same estimator when fed with its bitrate-$R$ quantized version. We demonstrate the usefulness of this connection by deriving various novel results for inference problems under compression constraints, including noisy source coding and limited-bitrate parameter estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge