Data-Driven Neural Polar Codes for Unknown Channels With and Without Memory

In this work, a novel data-driven methodology for designing polar codes for channels with and without memory is proposed. The methodology is suitable for the case where the channel is given as a "black-box" and the designer has access to the channel for generating observations of its inputs and outputs, but does not have access to the explicit channel model. The proposed method leverages the structure of the successive cancellation (SC) decoder to devise a neural SC (NSC) decoder. The NSC decoder uses neural networks (NNs) to replace the core elements of the original SC decoder, the check-node, the bit-node and the soft decision. Along with the NSC, we devise additional NN that embeds the channel outputs into the input space of the SC decoder. The proposed method is supported by theoretical guarantees that include the consistency of the NSC. Also, the NSC has computational complexity that does not grow with the channel memory size. This sets its main advantage over successive cancellation trellis (SCT) decoder for finite state channels (FSCs) that has complexity of $O(|\mathcal{S}|^3 N\log N)$, where $|\mathcal{S}|$ denotes the number of channel states. We demonstrate the performance of the proposed algorithms on memoryless channels and on channels with memory. The empirical results are compared with the optimal polar decoder, given by the SC and SCT decoders. We further show that our algorithms are applicable for the case where there SC and SCT decoders are not applicable.

Physics-Based Deep Learning for Fiber-Optic Communication Systems

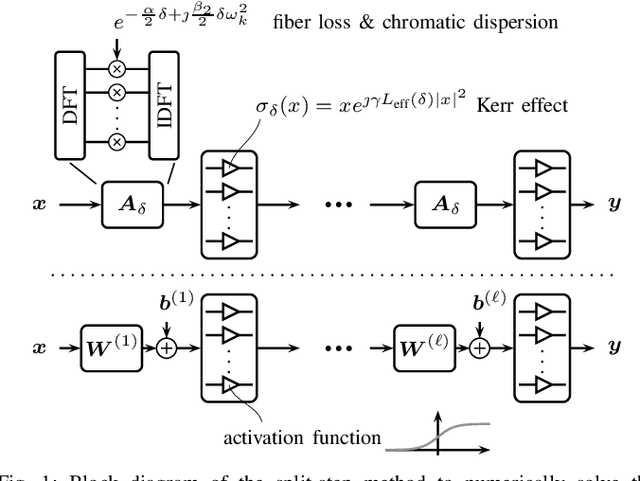
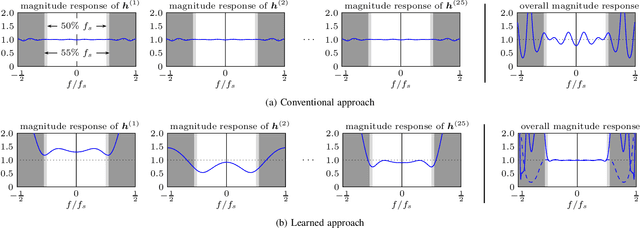
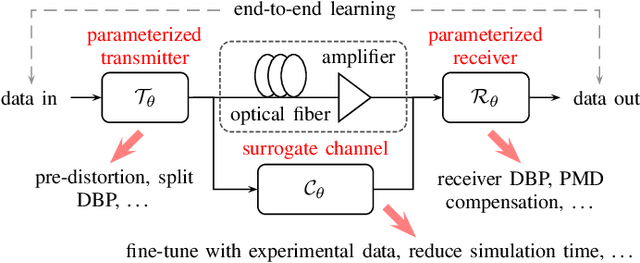
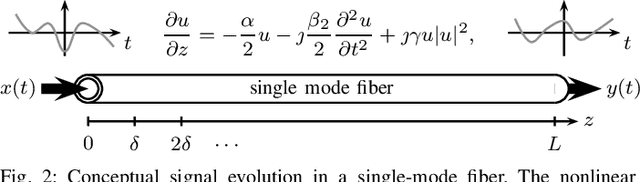
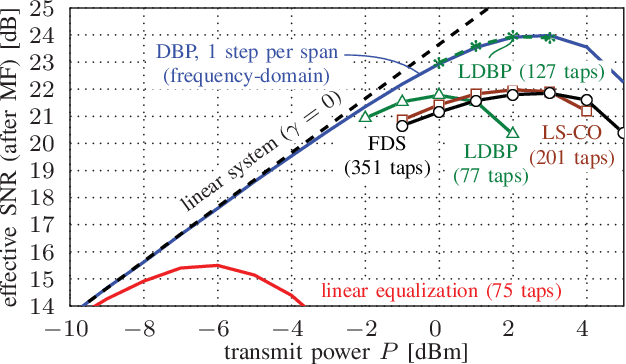
We propose a new machine-learning approach for fiber-optic communication systems whose signal propagation is governed by the nonlinear Schr\"odinger equation (NLSE). Our main observation is that the popular split-step method (SSM) for numerically solving the NLSE has essentially the same functional form as a deep multi-layer neural network; in both cases, one alternates linear steps and pointwise nonlinearities. We exploit this connection by parameterizing the SSM and viewing the linear steps as general linear functions, similar to the weight matrices in a neural network. The resulting physics-based machine-learning model has several advantages over "black-box" function approximators. For example, it allows us to examine and interpret the learned solutions in order to understand why they perform well. As an application, low-complexity nonlinear equalization is considered, where the task is to efficiently invert the NLSE. This is commonly referred to as digital backpropagation (DBP). Rather than employing neural networks, the proposed algorithm, dubbed learned DBP (LDBP), uses the physics-based model with trainable filters in each step and its complexity is reduced by progressively pruning filter taps during gradient descent. Our main finding is that the filters can be pruned to remarkably short lengths-as few as 3 taps/step-without sacrificing performance. As a result, the complexity can be reduced by orders of magnitude in comparison to prior work. By inspecting the filter responses, an additional theoretical justification for the learned parameter configurations is provided. Our work illustrates that combining data-driven optimization with existing domain knowledge can generate new insights into old communications problems.

Model-Based Machine Learning for Joint Digital Backpropagation and PMD Compensation

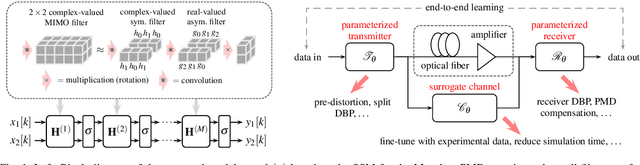
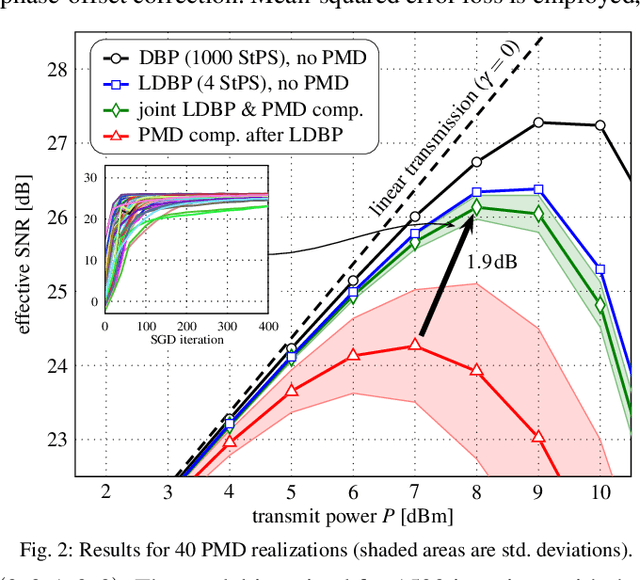
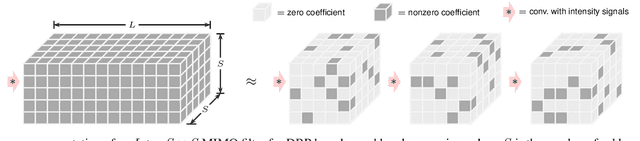
In this paper, we propose a model-based machine-learning approach for dual-polarization systems by parameterizing the split-step Fourier method for the Manakov-PMD equation. The resulting method combines hardware-friendly time-domain nonlinearity mitigation via the recently proposed learned digital backpropagation (LDBP) with distributed compensation of polarization-mode dispersion (PMD). We refer to the resulting approach as LDBP-PMD. We train LDBP-PMD on multiple PMD realizations and show that it converges within 1% of its peak dB performance after 428 training iterations on average, yielding a peak effective signal-to-noise ratio of only 0.30 dB below the PMD-free case. Similar to state-of-the-art lumped PMD compensation algorithms in practical systems, our approach does not assume any knowledge about the particular PMD realization along the link, nor any knowledge about the total accumulated PMD. This is a significant improvement compared to prior work on distributed PMD compensation, where knowledge about the accumulated PMD is typically assumed. We also compare different parameterization choices in terms of performance, complexity, and convergence behavior. Lastly, we demonstrate that the learned models can be successfully retrained after an abrupt change of the PMD realization along the fiber.

Pruning Neural Belief Propagation Decoders

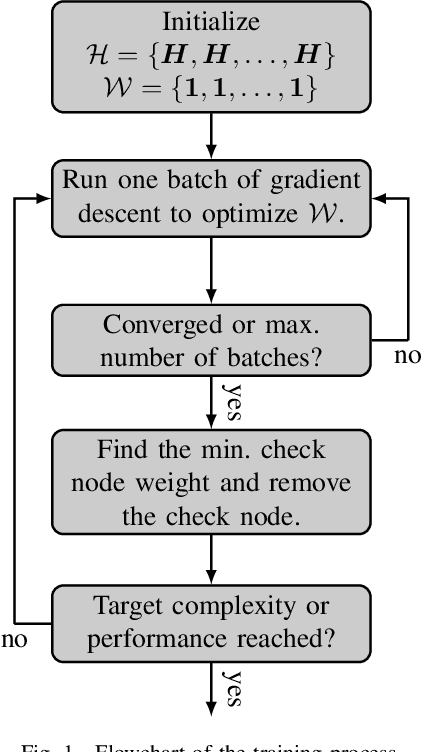
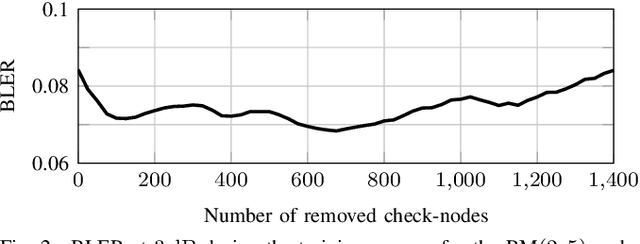
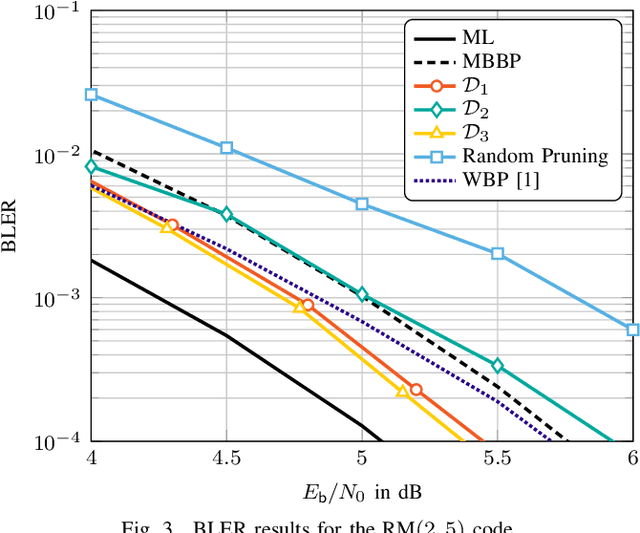
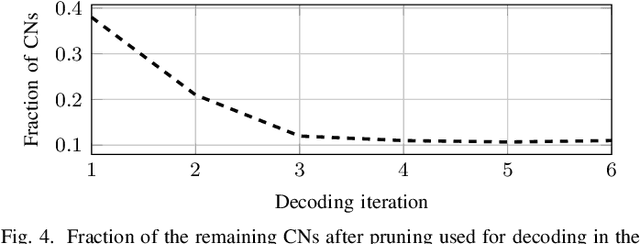
We consider near maximum-likelihood (ML) decoding of short linear block codes based on neural belief propagation (BP) decoding recently introduced by Nachmani et al.. While this method significantly outperforms conventional BP decoding, the underlying parity-check matrix may still limit the overall performance. In this paper, we introduce a method to tailor an overcomplete parity-check matrix to (neural) BP decoding using machine learning. We consider the weights in the Tanner graph as an indication of the importance of the connected check nodes (CNs) to decoding and use them to prune unimportant CNs. As the pruning is not tied over iterations, the final decoder uses a different parity-check matrix in each iteration. For Reed-Muller and short low-density parity-check codes, we achieve performance within 0.27 dB and 1.5 dB of the ML performance while reducing the complexity of the decoder.

Reinforcement Learning for Channel Coding: Learned Bit-Flipping Decoding

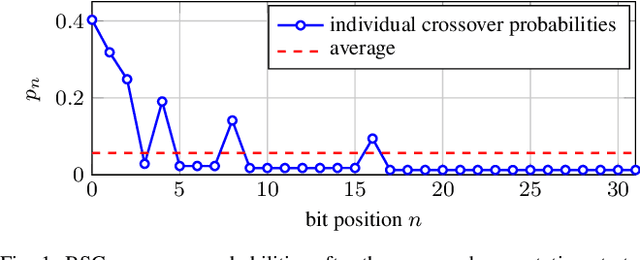
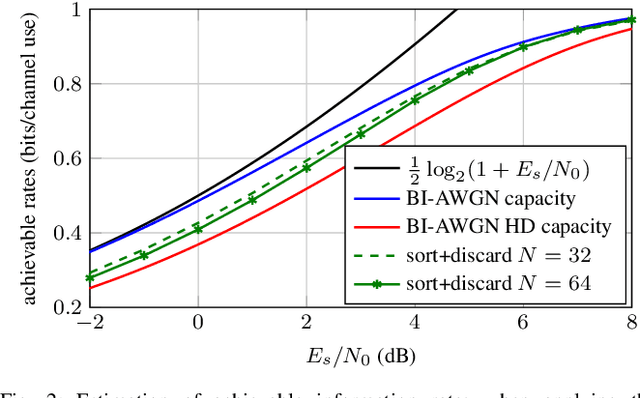
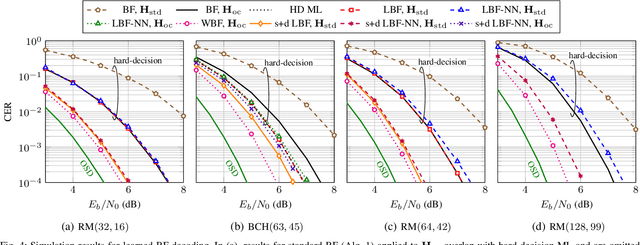
In this paper, we use reinforcement learning to find effective decoding strategies for binary linear codes. We start by reviewing several iterative decoding algorithms that involve a decision-making process at each step, including bit-flipping (BF) decoding, residual belief propagation, and anchor decoding. We then illustrate how such algorithms can be mapped to Markov decision processes allowing for data-driven learning of optimal decision strategies, rather than basing decisions on heuristics or intuition. As a case study, we consider BF decoding for both the binary symmetric and additive white Gaussian noise channel. Our results show that learned BF decoders can offer a range of performance--complexity trade-offs for the considered Reed--Muller and BCH codes, and achieve near-optimal performance in some cases. We also demonstrate learning convergence speed-ups when biasing the learning process towards correct decoding decisions, as opposed to relying only on random explorations and past knowledge.

Revisiting Multi-Step Nonlinearity Compensation with Machine Learning

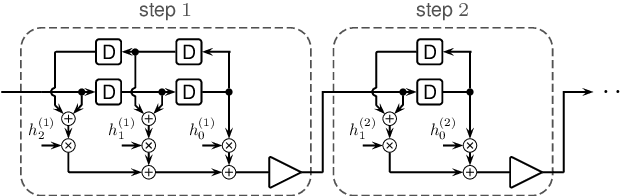
For the efficient compensation of fiber nonlinearity, one of the guiding principles appears to be: fewer steps are better and more efficient. We challenge this assumption and show that carefully designed multi-step approaches can lead to better performance-complexity trade-offs than their few-step counterparts.

Learned Belief-Propagation Decoding with Simple Scaling and SNR Adaptation

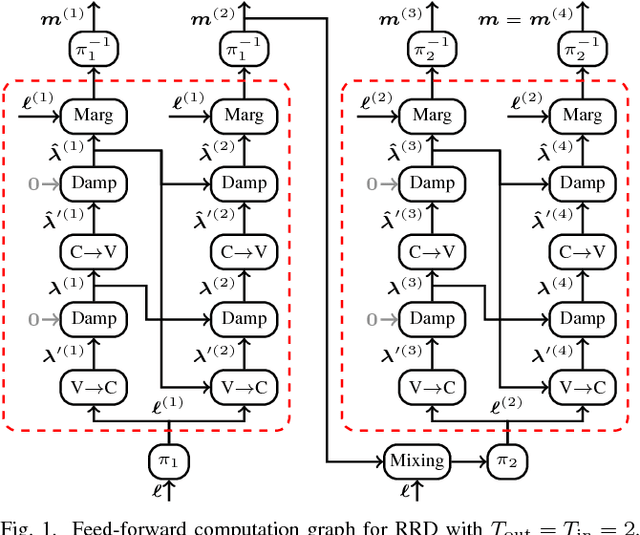
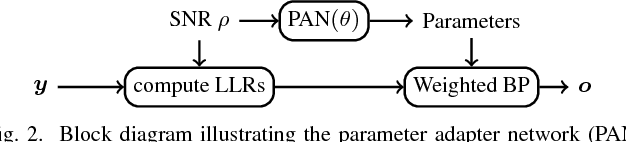
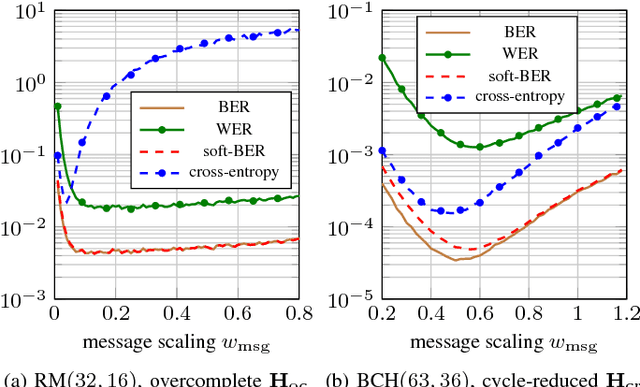
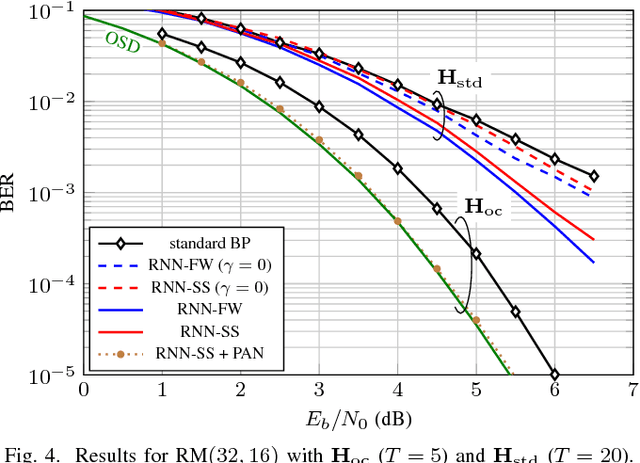
We consider the weighted belief-propagation (WBP) decoder recently proposed by Nachmani et al. where different weights are introduced for each Tanner graph edge and optimized using machine learning techniques. Our focus is on simple-scaling models that use the same weights across certain edges to reduce the storage and computational burden. The main contribution is to show that simple scaling with few parameters often achieves the same gain as the full parameterization. Moreover, several training improvements for WBP are proposed. For example, it is shown that minimizing average binary cross-entropy is suboptimal in general in terms of bit error rate (BER) and a new "soft-BER" loss is proposed which can lead to better performance. We also investigate parameter adapter networks (PANs) that learn the relation between the signal-to-noise ratio and the WBP parameters. As an example, for the (32,16) Reed-Muller code with a highly redundant parity-check matrix, training a PAN with soft-BER loss gives near-maximum-likelihood performance assuming simple scaling with only three parameters.

What Can Machine Learning Teach Us about Communications?

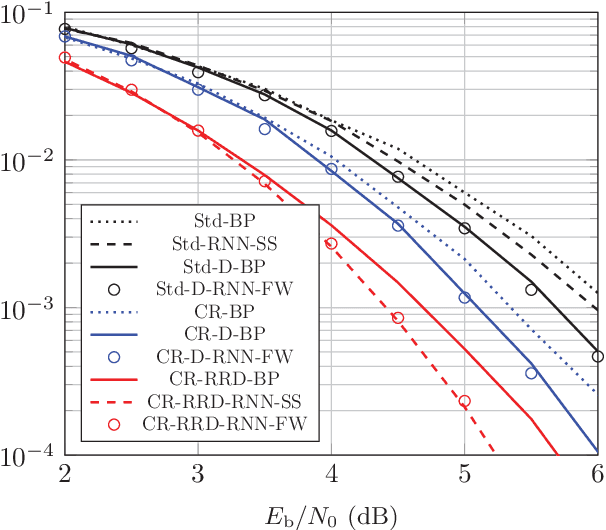
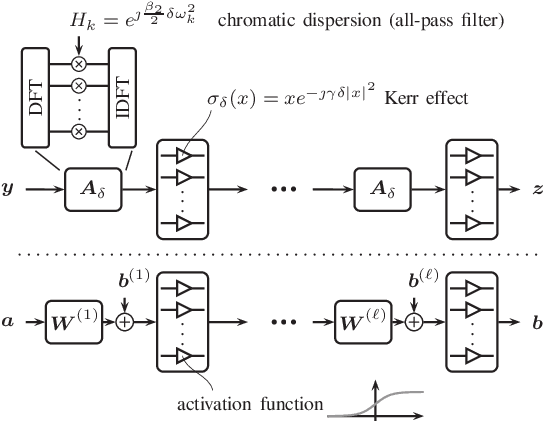
Rapid improvements in machine learning over the past decade are beginning to have far-reaching effects. For communications, engineers with limited domain expertise can now use off-the-shelf learning packages to design high-performance systems based on simulations. Prior to the current revolution in machine learning, the majority of communication engineers were quite aware that system parameters (such as filter coefficients) could be learned using stochastic gradient descent. It was not at all clear, however, that more complicated parts of the system architecture could be learned as well. In this paper, we discuss the application of machine-learning techniques to two communications problems and focus on what can be learned from the resulting systems. We were pleasantly surprised that the observed gains in one example have a simple explanation that only became clear in hindsight. In essence, deep learning discovered a simple and effective strategy that had not been considered earlier.

Wideband Time-Domain Digital Backpropagation via Subband Processing and Deep Learning

We propose a low-complexity sub-banded DSP architecture for digital backpropagation where the walk-off effect is compensated using simple delay elements. For a simulated 96-Gbaud signal and 2500 km optical link, our method achieves a 2.8 dB SNR improvement over linear equalization.

ASIC Implementation of Time-Domain Digital Backpropagation with Deep-Learned Chromatic Dispersion Filters

We consider time-domain digital backpropagation with chromatic dispersion filters jointly optimized and quantized using machine-learning techniques. Compared to the baseline implementations, we show improved BER performance and >40% power dissipation reductions in 28-nm CMOS.