Learned Belief-Propagation Decoding with Simple Scaling and SNR Adaptation
Paper and Code
Jan 24, 2019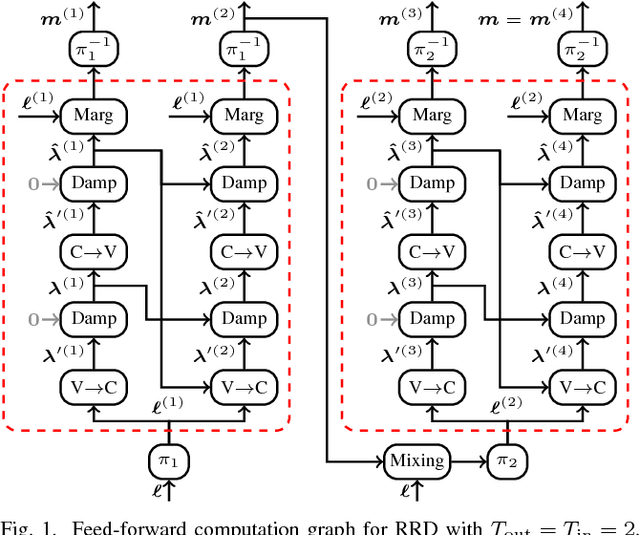
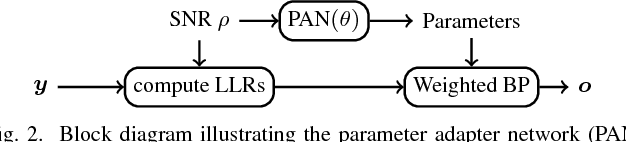
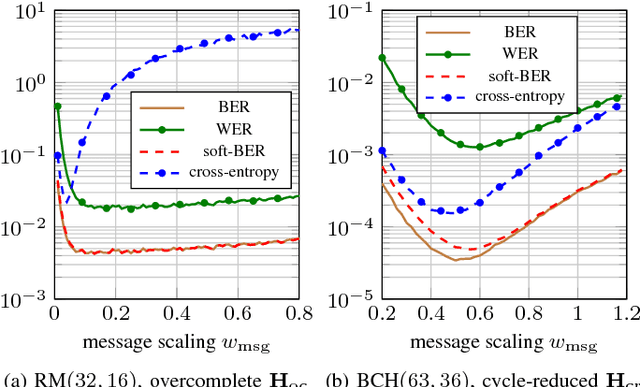
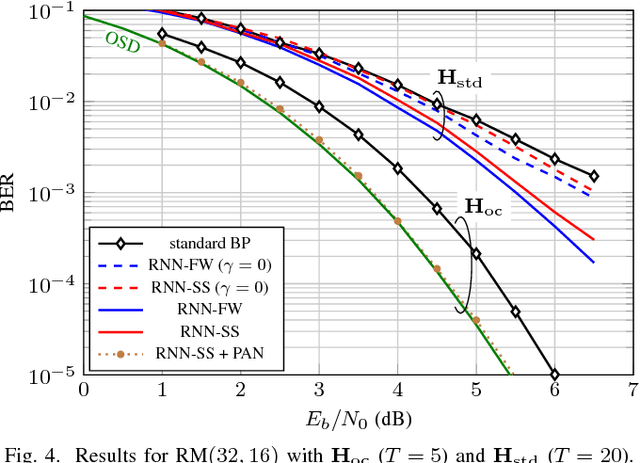
We consider the weighted belief-propagation (WBP) decoder recently proposed by Nachmani et al. where different weights are introduced for each Tanner graph edge and optimized using machine learning techniques. Our focus is on simple-scaling models that use the same weights across certain edges to reduce the storage and computational burden. The main contribution is to show that simple scaling with few parameters often achieves the same gain as the full parameterization. Moreover, several training improvements for WBP are proposed. For example, it is shown that minimizing average binary cross-entropy is suboptimal in general in terms of bit error rate (BER) and a new "soft-BER" loss is proposed which can lead to better performance. We also investigate parameter adapter networks (PANs) that learn the relation between the signal-to-noise ratio and the WBP parameters. As an example, for the (32,16) Reed-Muller code with a highly redundant parity-check matrix, training a PAN with soft-BER loss gives near-maximum-likelihood performance assuming simple scaling with only three parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge