Physics-Based Deep Learning for Fiber-Optic Communication Systems

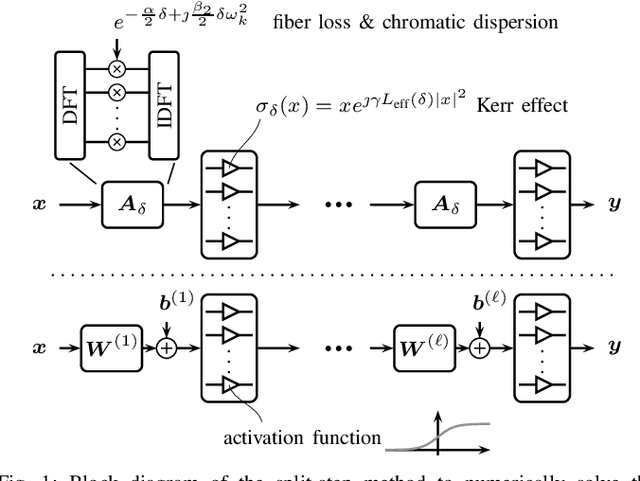
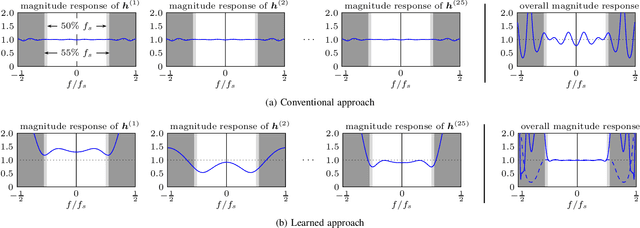
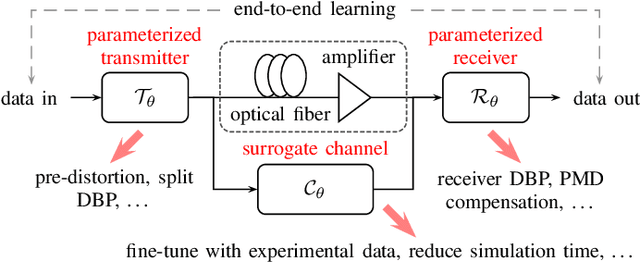
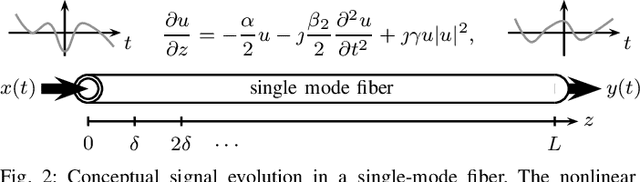
We propose a new machine-learning approach for fiber-optic communication systems whose signal propagation is governed by the nonlinear Schr\"odinger equation (NLSE). Our main observation is that the popular split-step method (SSM) for numerically solving the NLSE has essentially the same functional form as a deep multi-layer neural network; in both cases, one alternates linear steps and pointwise nonlinearities. We exploit this connection by parameterizing the SSM and viewing the linear steps as general linear functions, similar to the weight matrices in a neural network. The resulting physics-based machine-learning model has several advantages over "black-box" function approximators. For example, it allows us to examine and interpret the learned solutions in order to understand why they perform well. As an application, low-complexity nonlinear equalization is considered, where the task is to efficiently invert the NLSE. This is commonly referred to as digital backpropagation (DBP). Rather than employing neural networks, the proposed algorithm, dubbed learned DBP (LDBP), uses the physics-based model with trainable filters in each step and its complexity is reduced by progressively pruning filter taps during gradient descent. Our main finding is that the filters can be pruned to remarkably short lengths-as few as 3 taps/step-without sacrificing performance. As a result, the complexity can be reduced by orders of magnitude in comparison to prior work. By inspecting the filter responses, an additional theoretical justification for the learned parameter configurations is provided. Our work illustrates that combining data-driven optimization with existing domain knowledge can generate new insights into old communications problems.