Data-Driven Neural Polar Codes for Unknown Channels With and Without Memory

In this work, a novel data-driven methodology for designing polar codes for channels with and without memory is proposed. The methodology is suitable for the case where the channel is given as a "black-box" and the designer has access to the channel for generating observations of its inputs and outputs, but does not have access to the explicit channel model. The proposed method leverages the structure of the successive cancellation (SC) decoder to devise a neural SC (NSC) decoder. The NSC decoder uses neural networks (NNs) to replace the core elements of the original SC decoder, the check-node, the bit-node and the soft decision. Along with the NSC, we devise additional NN that embeds the channel outputs into the input space of the SC decoder. The proposed method is supported by theoretical guarantees that include the consistency of the NSC. Also, the NSC has computational complexity that does not grow with the channel memory size. This sets its main advantage over successive cancellation trellis (SCT) decoder for finite state channels (FSCs) that has complexity of $O(|\mathcal{S}|^3 N\log N)$, where $|\mathcal{S}|$ denotes the number of channel states. We demonstrate the performance of the proposed algorithms on memoryless channels and on channels with memory. The empirical results are compared with the optimal polar decoder, given by the SC and SCT decoders. We further show that our algorithms are applicable for the case where there SC and SCT decoders are not applicable.

Data-Driven Optimization of Directed Information over Discrete Alphabets

Directed information (DI) is a fundamental measure for the study and analysis of sequential stochastic models. In particular, when optimized over input distributions it characterizes the capacity of general communication channels. However, analytic computation of DI is typically intractable and existing optimization techniques over discrete input alphabets require knowledge of the channel model, which renders them inapplicable when only samples are available. To overcome these limitations, we propose a novel estimation-optimization framework for DI over discrete input spaces. We formulate DI optimization as a Markov decision process and leverage reinforcement learning techniques to optimize a deep generative model of the input process probability mass function (PMF). Combining this optimizer with the recently developed DI neural estimator, we obtain an end-to-end estimation-optimization algorithm which is applied to estimating the (feedforward and feedback) capacity of various discrete channels with memory. Furthermore, we demonstrate how to use the optimized PMF model to (i) obtain theoretical bounds on the feedback capacity of unifilar finite-state channels; and (ii) perform probabilistic shaping of constellations in the peak power-constrained additive white Gaussian noise channel.

Capacity of Continuous Channels with Memory via Directed Information Neural Estimator

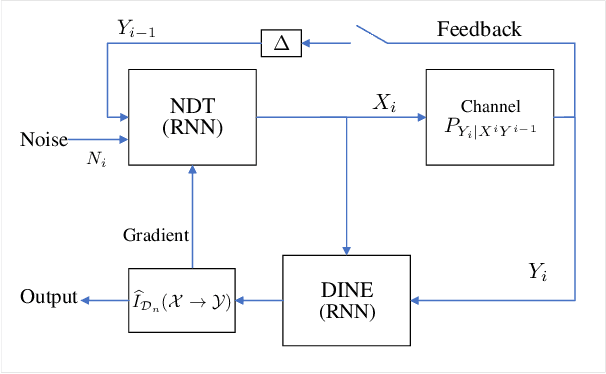
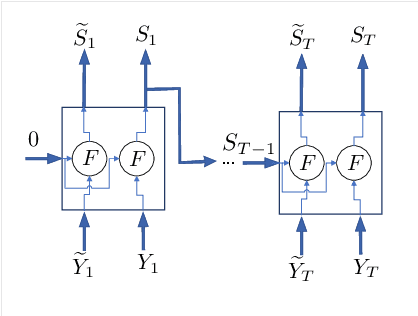
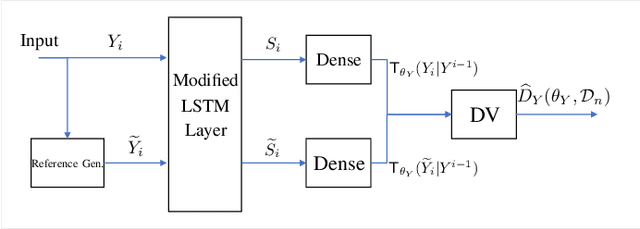
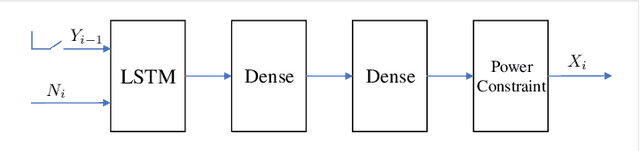
Calculating the capacity (with or without feedback) of channels with memory and continuous alphabets is a challenging task. It requires optimizing the directed information rate over all channel input distributions. The objective is a multi-letter expression, whose analytic solution is only known for a few specific cases. When no analytic solution is present or the channel model is unknown, there is no unified framework for calculating or even approximating capacity. This work proposes a novel capacity estimation algorithm that treats the channel as a `black-box', both when feedback is or is not present. The algorithm has two main ingredients: (i) a neural distribution transformer (NDT) model that shapes a noise variable into the channel input distribution, which we are able to sample, and (ii) the directed information neural estimator (DINE) that estimates the communication rate of the current NDT model. These models are trained by an alternating maximization procedure to both estimate the channel capacity and obtain an NDT for the optimal input distribution. The method is demonstrated on the moving average additive Gaussian noise channel, where it is shown that both the capacity and feedback capacity are estimated without knowledge of the channel transition kernel. The proposed estimation framework opens the door to a myriad of capacity approximation results for continuous alphabet channels that were inaccessible until now.

Computing the Feedback Capacity of Finite State Channels using Reinforcement Learning

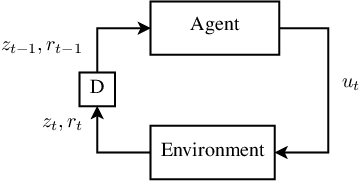
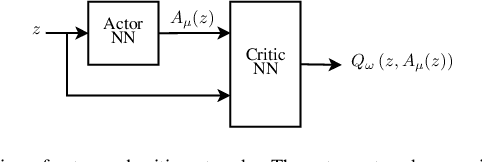
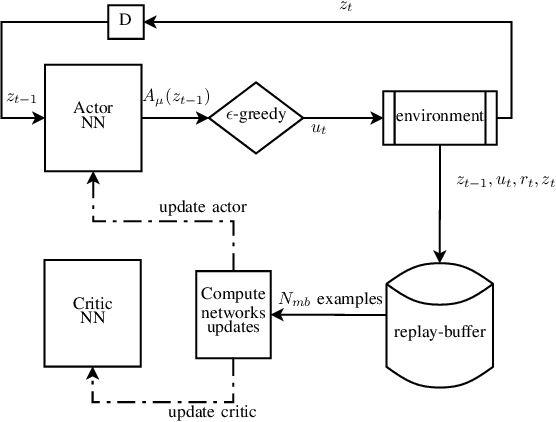
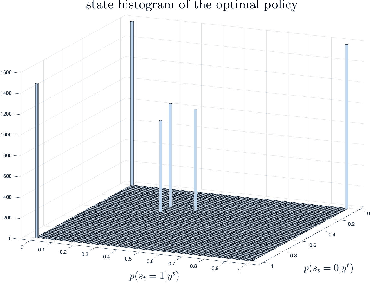
In this paper, we propose a novel method to compute the feedback capacity of channels with memory using reinforcement learning (RL). In RL, one seeks to maximize cumulative rewards collected in a sequential decision-making environment. This is done by collecting samples of the underlying environment and using them to learn the optimal decision rule. The main advantage of this approach is its computational efficiency, even in high dimensional problems. Hence, RL can be used to estimate numerically the feedback capacity of unifilar finite state channels (FSCs) with large alphabet size. The outcome of the RL algorithm sheds light on the properties of the optimal decision rule, which in our case, is the optimal input distribution of the channel. These insights can be converted into analytic, single-letter capacity expressions by solving corresponding lower and upper bounds. We demonstrate the efficiency of this method by analytically solving the feedback capacity of the well-known Ising channel with a ternary alphabet. We also provide a simple coding scheme that achieves the feedback capacity.

Gradual Learning of Recurrent Neural Networks

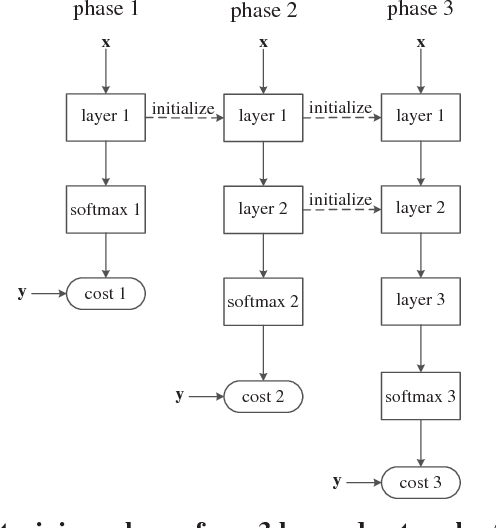
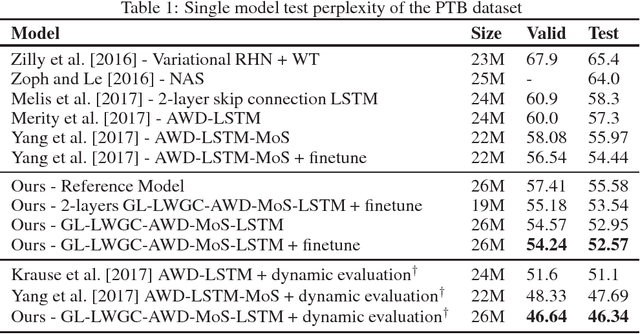
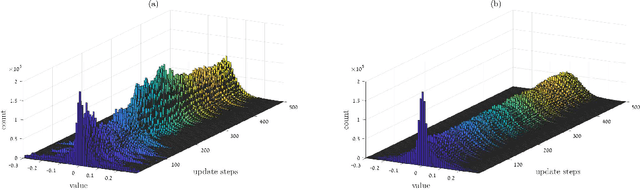
Recurrent Neural Networks (RNNs) achieve state-of-the-art results in many sequence-to-sequence modeling tasks. However, RNNs are difficult to train and tend to suffer from overfitting. Motivated by the Data Processing Inequality (DPI), we formulate the multi-layered network as a Markov chain, introducing a training method that comprises training the network gradually and using layer-wise gradient clipping. We found that applying our methods, combined with previously introduced regularization and optimization methods, resulted in improvements in state-of-the-art architectures operating in language modeling tasks.