Capacity of Continuous Channels with Memory via Directed Information Neural Estimator

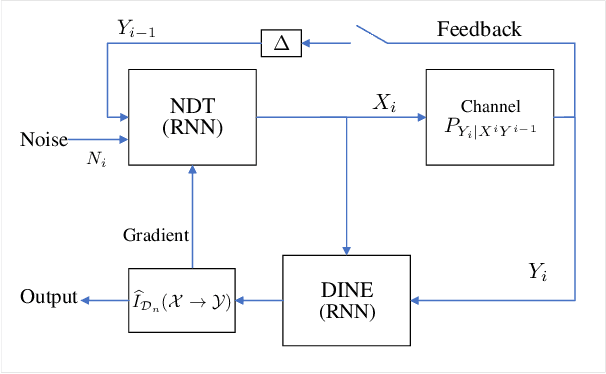
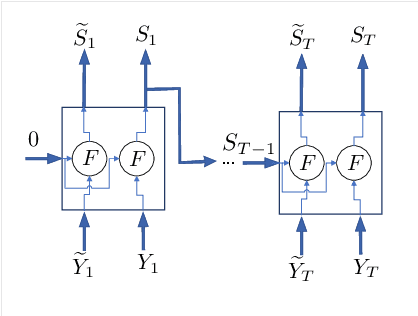
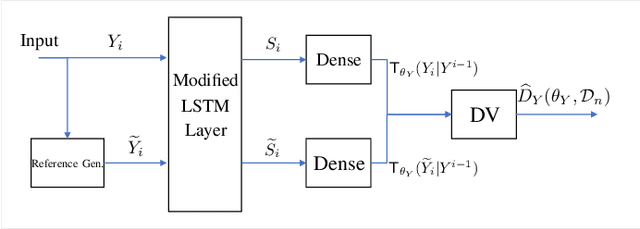
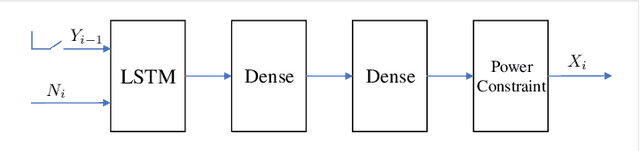
Calculating the capacity (with or without feedback) of channels with memory and continuous alphabets is a challenging task. It requires optimizing the directed information rate over all channel input distributions. The objective is a multi-letter expression, whose analytic solution is only known for a few specific cases. When no analytic solution is present or the channel model is unknown, there is no unified framework for calculating or even approximating capacity. This work proposes a novel capacity estimation algorithm that treats the channel as a `black-box', both when feedback is or is not present. The algorithm has two main ingredients: (i) a neural distribution transformer (NDT) model that shapes a noise variable into the channel input distribution, which we are able to sample, and (ii) the directed information neural estimator (DINE) that estimates the communication rate of the current NDT model. These models are trained by an alternating maximization procedure to both estimate the channel capacity and obtain an NDT for the optimal input distribution. The method is demonstrated on the moving average additive Gaussian noise channel, where it is shown that both the capacity and feedback capacity are estimated without knowledge of the channel transition kernel. The proposed estimation framework opens the door to a myriad of capacity approximation results for continuous alphabet channels that were inaccessible until now.

Computing the Feedback Capacity of Finite State Channels using Reinforcement Learning

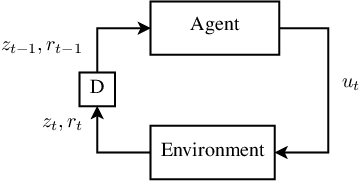
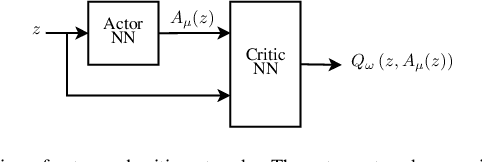
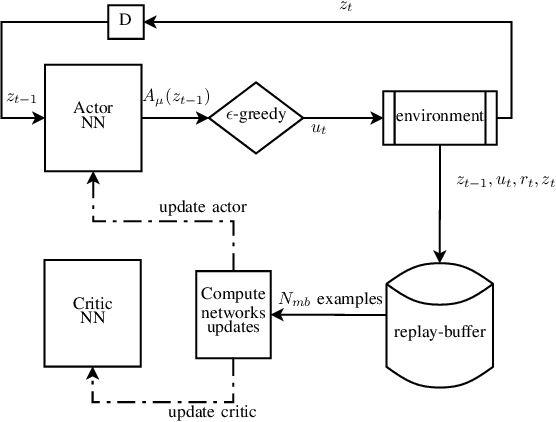
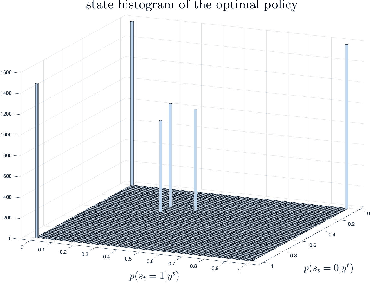
In this paper, we propose a novel method to compute the feedback capacity of channels with memory using reinforcement learning (RL). In RL, one seeks to maximize cumulative rewards collected in a sequential decision-making environment. This is done by collecting samples of the underlying environment and using them to learn the optimal decision rule. The main advantage of this approach is its computational efficiency, even in high dimensional problems. Hence, RL can be used to estimate numerically the feedback capacity of unifilar finite state channels (FSCs) with large alphabet size. The outcome of the RL algorithm sheds light on the properties of the optimal decision rule, which in our case, is the optimal input distribution of the channel. These insights can be converted into analytic, single-letter capacity expressions by solving corresponding lower and upper bounds. We demonstrate the efficiency of this method by analytically solving the feedback capacity of the well-known Ising channel with a ternary alphabet. We also provide a simple coding scheme that achieves the feedback capacity.