HeavyWater and SimplexWater: Watermarking Low-Entropy Text Distributions

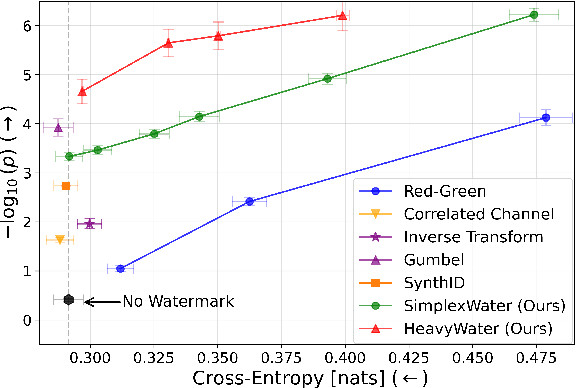
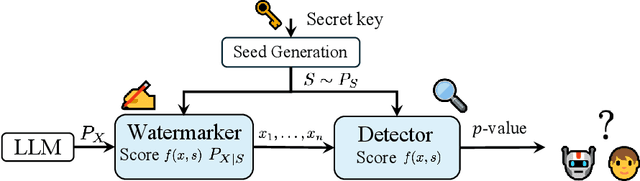
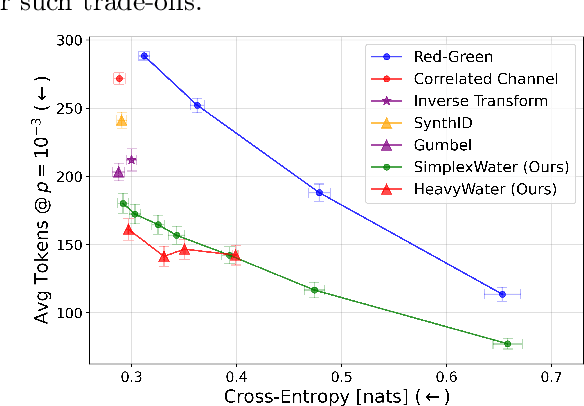
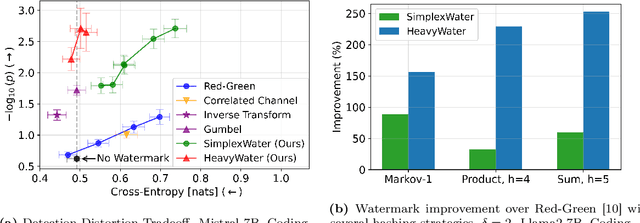
Large language model (LLM) watermarks enable authentication of text provenance, curb misuse of machine-generated text, and promote trust in AI systems. Current watermarks operate by changing the next-token predictions output by an LLM. The updated (i.e., watermarked) predictions depend on random side information produced, for example, by hashing previously generated tokens. LLM watermarking is particularly challenging in low-entropy generation tasks - such as coding - where next-token predictions are near-deterministic. In this paper, we propose an optimization framework for watermark design. Our goal is to understand how to most effectively use random side information in order to maximize the likelihood of watermark detection and minimize the distortion of generated text. Our analysis informs the design of two new watermarks: HeavyWater and SimplexWater. Both watermarks are tunable, gracefully trading-off between detection accuracy and text distortion. They can also be applied to any LLM and are agnostic to side information generation. We examine the performance of HeavyWater and SimplexWater through several benchmarks, demonstrating that they can achieve high watermark detection accuracy with minimal compromise of text generation quality, particularly in the low-entropy regime. Our theoretical analysis also reveals surprising new connections between LLM watermarking and coding theory. The code implementation can be found in https://github.com/DorTsur/HeavyWater_SimplexWater

Optimized Couplings for Watermarking Large Language Models

Large-language models (LLMs) are now able to produce text that is, in many cases, seemingly indistinguishable from human-generated content. This has fueled the development of watermarks that imprint a ``signal'' in LLM-generated text with minimal perturbation of an LLM's output. This paper provides an analysis of text watermarking in a one-shot setting. Through the lens of hypothesis testing with side information, we formulate and analyze the fundamental trade-off between watermark detection power and distortion in generated textual quality. We argue that a key component in watermark design is generating a coupling between the side information shared with the watermark detector and a random partition of the LLM vocabulary. Our analysis identifies the optimal coupling and randomization strategy under the worst-case LLM next-token distribution that satisfies a min-entropy constraint. We provide a closed-form expression of the resulting detection rate under the proposed scheme and quantify the cost in a max-min sense. Finally, we provide an array of numerical results, comparing the proposed scheme with the theoretical optimum and existing schemes, in both synthetic data and LLM watermarking. Our code is available at https://github.com/Carol-Long/CC_Watermark

Efficient Time Series Forecasting via Hyper-Complex Models and Frequency Aggregation

Time series forecasting is a long-standing problem in statistics and machine learning. One of the key challenges is processing sequences with long-range dependencies. To that end, a recent line of work applied the short-time Fourier transform (STFT), which partitions the sequence into multiple subsequences and applies a Fourier transform to each separately. We propose the Frequency Information Aggregation (FIA)-Net, which is based on a novel complex-valued MLP architecture that aggregates adjacent window information in the frequency domain. To further increase the receptive field of the FIA-Net, we treat the set of windows as hyper-complex (HC) valued vectors and employ HC algebra to efficiently combine information from all STFT windows altogether. Using the HC-MLP backbone allows for improved handling of sequences with long-term dependence. Furthermore, due to the nature of HC operations, the HC-MLP uses up to three times fewer parameters than the equivalent standard window aggregation method. We evaluate the FIA-Net on various time-series benchmarks and show that the proposed methodologies outperform existing state of the art methods in terms of both accuracy and efficiency. Our code is publicly available on https://anonymous.4open.science/r/research-1803/.

TREET: TRansfer Entropy Estimation via Transformer

Transfer entropy (TE) is a measurement in information theory that reveals the directional flow of information between processes, providing valuable insights for a wide range of real-world applications. This work proposes Transfer Entropy Estimation via Transformers (TREET), a novel transformer-based approach for estimating the TE for stationary processes. The proposed approach employs Donsker-Vardhan (DV) representation to TE and leverages the attention mechanism for the task of neural estimation. We propose a detailed theoretical and empirical study of the TREET, comparing it to existing methods. To increase its applicability, we design an estimated TE optimization scheme that is motivated by the functional representation lemma. Afterwards, we take advantage of the joint optimization scheme to optimize the capacity of communication channels with memory, which is a canonical optimization problem in information theory, and show the memory capabilities of our estimator. Finally, we apply TREET to real-world feature analysis. Our work, applied with state-of-the-art deep learning methods, opens a new door for communication problems which are yet to be solved.

Max-Sliced Mutual Information

Quantifying the dependence between high-dimensional random variables is central to statistical learning and inference. Two classical methods are canonical correlation analysis (CCA), which identifies maximally correlated projected versions of the original variables, and Shannon's mutual information, which is a universal dependence measure that also captures high-order dependencies. However, CCA only accounts for linear dependence, which may be insufficient for certain applications, while mutual information is often infeasible to compute/estimate in high dimensions. This work proposes a middle ground in the form of a scalable information-theoretic generalization of CCA, termed max-sliced mutual information (mSMI). mSMI equals the maximal mutual information between low-dimensional projections of the high-dimensional variables, which reduces back to CCA in the Gaussian case. It enjoys the best of both worlds: capturing intricate dependencies in the data while being amenable to fast computation and scalable estimation from samples. We show that mSMI retains favorable structural properties of Shannon's mutual information, like variational forms and identification of independence. We then study statistical estimation of mSMI, propose an efficiently computable neural estimator, and couple it with formal non-asymptotic error bounds. We present experiments that demonstrate the utility of mSMI for several tasks, encompassing independence testing, multi-view representation learning, algorithmic fairness, and generative modeling. We observe that mSMI consistently outperforms competing methods with little-to-no computational overhead.

Data-Driven Optimization of Directed Information over Discrete Alphabets

Directed information (DI) is a fundamental measure for the study and analysis of sequential stochastic models. In particular, when optimized over input distributions it characterizes the capacity of general communication channels. However, analytic computation of DI is typically intractable and existing optimization techniques over discrete input alphabets require knowledge of the channel model, which renders them inapplicable when only samples are available. To overcome these limitations, we propose a novel estimation-optimization framework for DI over discrete input spaces. We formulate DI optimization as a Markov decision process and leverage reinforcement learning techniques to optimize a deep generative model of the input process probability mass function (PMF). Combining this optimizer with the recently developed DI neural estimator, we obtain an end-to-end estimation-optimization algorithm which is applied to estimating the (feedforward and feedback) capacity of various discrete channels with memory. Furthermore, we demonstrate how to use the optimized PMF model to (i) obtain theoretical bounds on the feedback capacity of unifilar finite-state channels; and (ii) perform probabilistic shaping of constellations in the peak power-constrained additive white Gaussian noise channel.

Capacity of Continuous Channels with Memory via Directed Information Neural Estimator

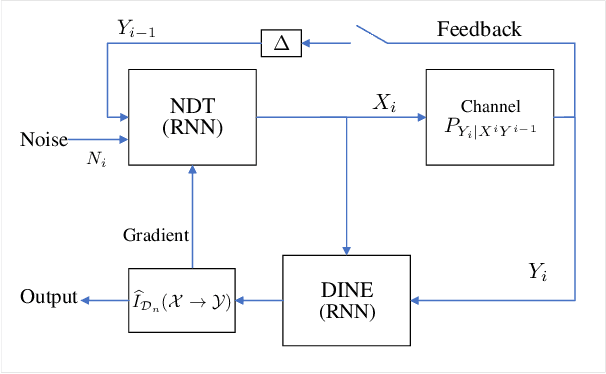
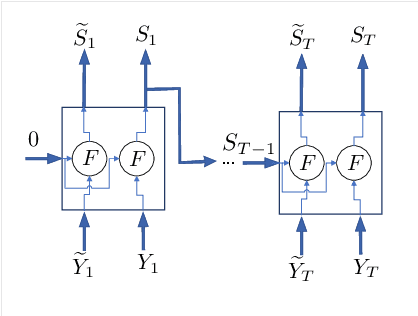
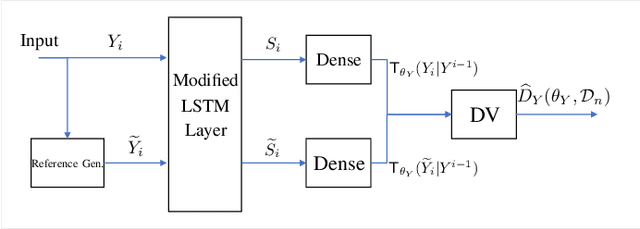
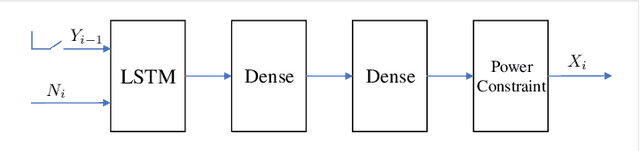
Calculating the capacity (with or without feedback) of channels with memory and continuous alphabets is a challenging task. It requires optimizing the directed information rate over all channel input distributions. The objective is a multi-letter expression, whose analytic solution is only known for a few specific cases. When no analytic solution is present or the channel model is unknown, there is no unified framework for calculating or even approximating capacity. This work proposes a novel capacity estimation algorithm that treats the channel as a `black-box', both when feedback is or is not present. The algorithm has two main ingredients: (i) a neural distribution transformer (NDT) model that shapes a noise variable into the channel input distribution, which we are able to sample, and (ii) the directed information neural estimator (DINE) that estimates the communication rate of the current NDT model. These models are trained by an alternating maximization procedure to both estimate the channel capacity and obtain an NDT for the optimal input distribution. The method is demonstrated on the moving average additive Gaussian noise channel, where it is shown that both the capacity and feedback capacity are estimated without knowledge of the channel transition kernel. The proposed estimation framework opens the door to a myriad of capacity approximation results for continuous alphabet channels that were inaccessible until now.