Claudio Mayrink Verdun
Inference-Time Reward Hacking in Large Language Models
Jun 24, 2025Abstract:A common paradigm to improve the performance of large language models is optimizing for a reward model. Reward models assign a numerical score to LLM outputs indicating, for example, which response would likely be preferred by a user or is most aligned with safety goals. However, reward models are never perfect. They inevitably function as proxies for complex desiderata such as correctness, helpfulness, and safety. By overoptimizing for a misspecified reward, we can subvert intended alignment goals and reduce overall performance -- a phenomenon commonly referred to as reward hacking. In this work, we characterize reward hacking in inference-time alignment and demonstrate when and how we can mitigate it by hedging on the proxy reward. We study this phenomenon under Best-of-$n$ (BoN) and Soft-Best-of-$n$ (SBoN), and we introduce Best-of-Poisson (BoP) that provides an efficient, near-exact approximation of the optimal reward-KL divergence policy at inference time. We show that the characteristic pattern of hacking as observed in practice (where the true reward first increases before declining) is an inevitable property of a broad class of inference-time mechanisms, including BoN and BoP. To counter this effect, hedging offers a tactical choice to avoid placing undue confidence in high but potentially misleading proxy reward signals. We introduce HedgeTune, an efficient algorithm to find the optimal inference-time parameter and avoid reward hacking. We demonstrate through experiments that hedging mitigates reward hacking and achieves superior distortion-reward tradeoffs with minimal computational overhead.
HeavyWater and SimplexWater: Watermarking Low-Entropy Text Distributions
Jun 06, 2025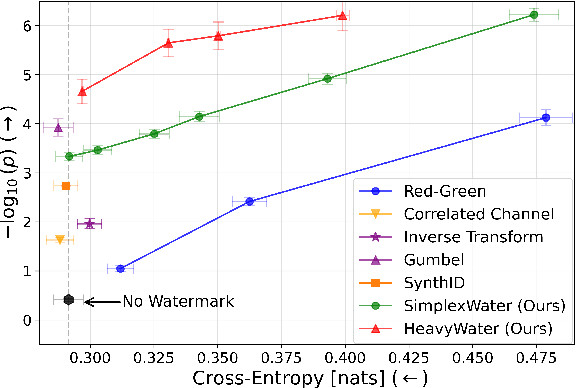
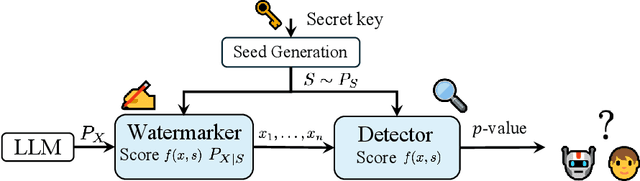
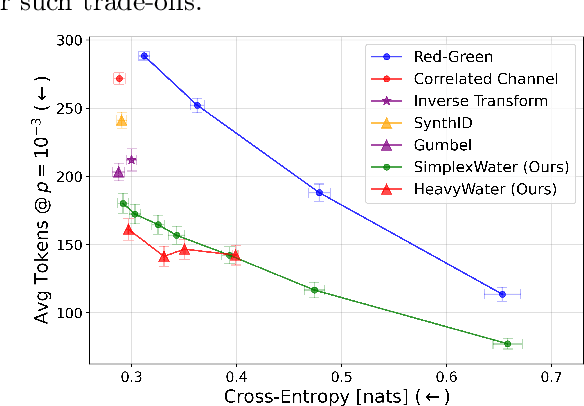
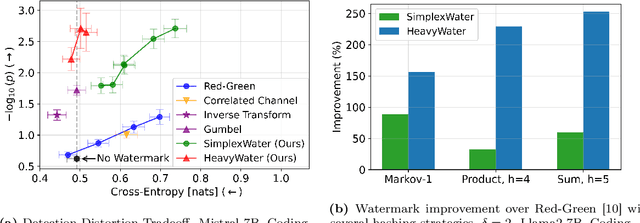
Abstract:Large language model (LLM) watermarks enable authentication of text provenance, curb misuse of machine-generated text, and promote trust in AI systems. Current watermarks operate by changing the next-token predictions output by an LLM. The updated (i.e., watermarked) predictions depend on random side information produced, for example, by hashing previously generated tokens. LLM watermarking is particularly challenging in low-entropy generation tasks - such as coding - where next-token predictions are near-deterministic. In this paper, we propose an optimization framework for watermark design. Our goal is to understand how to most effectively use random side information in order to maximize the likelihood of watermark detection and minimize the distortion of generated text. Our analysis informs the design of two new watermarks: HeavyWater and SimplexWater. Both watermarks are tunable, gracefully trading-off between detection accuracy and text distortion. They can also be applied to any LLM and are agnostic to side information generation. We examine the performance of HeavyWater and SimplexWater through several benchmarks, demonstrating that they can achieve high watermark detection accuracy with minimal compromise of text generation quality, particularly in the low-entropy regime. Our theoretical analysis also reveals surprising new connections between LLM watermarking and coding theory. The code implementation can be found in https://github.com/DorTsur/HeavyWater_SimplexWater
Multi-Group Proportional Representation for Text-to-Image Models
May 29, 2025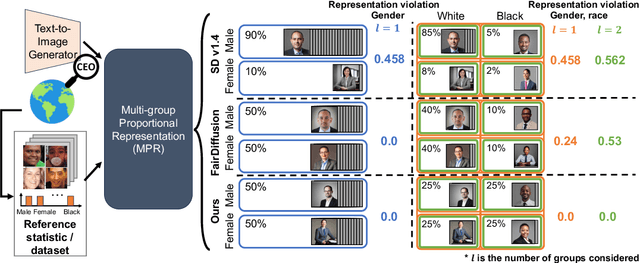
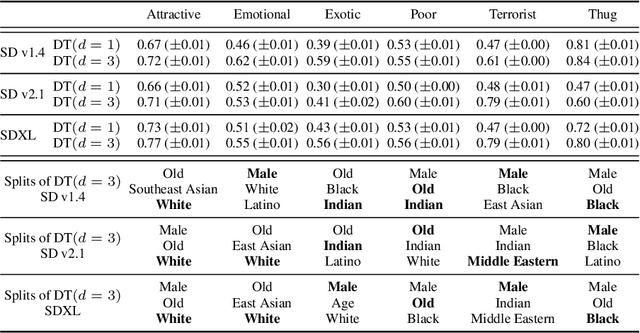
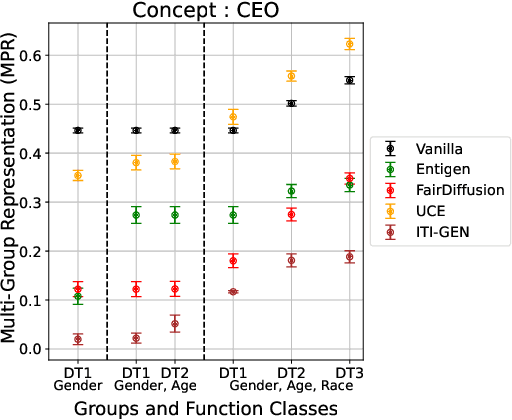
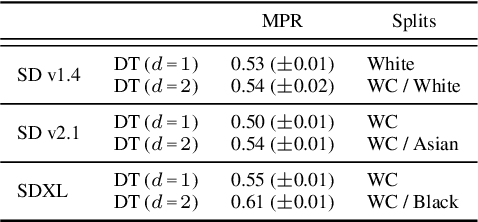
Abstract:Text-to-image (T2I) generative models can create vivid, realistic images from textual descriptions. As these models proliferate, they expose new concerns about their ability to represent diverse demographic groups, propagate stereotypes, and efface minority populations. Despite growing attention to the "safe" and "responsible" design of artificial intelligence (AI), there is no established methodology to systematically measure and control representational harms in image generation. This paper introduces a novel framework to measure the representation of intersectional groups in images generated by T2I models by applying the Multi-Group Proportional Representation (MPR) metric. MPR evaluates the worst-case deviation of representation statistics across given population groups in images produced by a generative model, allowing for flexible and context-specific measurements based on user requirements. We also develop an algorithm to optimize T2I models for this metric. Through experiments, we demonstrate that MPR can effectively measure representation statistics across multiple intersectional groups and, when used as a training objective, can guide models toward a more balanced generation across demographic groups while maintaining generation quality.
GradPCA: Leveraging NTK Alignment for Reliable Out-of-Distribution Detection
May 21, 2025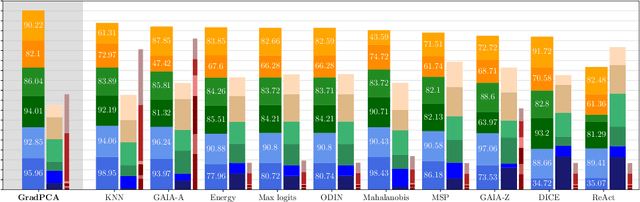
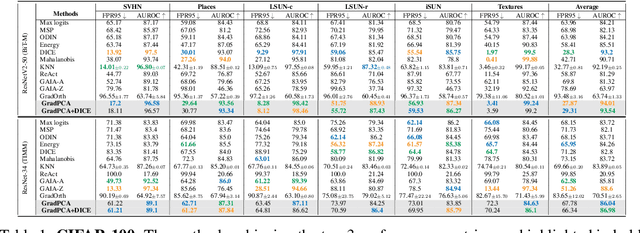

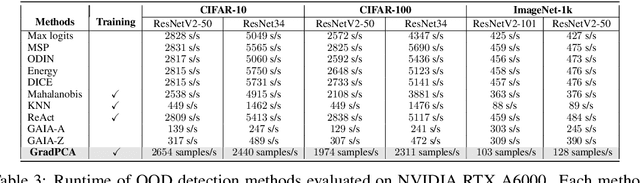
Abstract:We introduce GradPCA, an Out-of-Distribution (OOD) detection method that exploits the low-rank structure of neural network gradients induced by Neural Tangent Kernel (NTK) alignment. GradPCA applies Principal Component Analysis (PCA) to gradient class-means, achieving more consistent performance than existing methods across standard image classification benchmarks. We provide a theoretical perspective on spectral OOD detection in neural networks to support GradPCA, highlighting feature-space properties that enable effective detection and naturally emerge from NTK alignment. Our analysis further reveals that feature quality -- particularly the use of pretrained versus non-pretrained representations -- plays a crucial role in determining which detectors will succeed. Extensive experiments validate the strong performance of GradPCA, and our theoretical framework offers guidance for designing more principled spectral OOD detectors.
Optimized Couplings for Watermarking Large Language Models
May 13, 2025Abstract:Large-language models (LLMs) are now able to produce text that is, in many cases, seemingly indistinguishable from human-generated content. This has fueled the development of watermarks that imprint a ``signal'' in LLM-generated text with minimal perturbation of an LLM's output. This paper provides an analysis of text watermarking in a one-shot setting. Through the lens of hypothesis testing with side information, we formulate and analyze the fundamental trade-off between watermark detection power and distortion in generated textual quality. We argue that a key component in watermark design is generating a coupling between the side information shared with the watermark detector and a random partition of the LLM vocabulary. Our analysis identifies the optimal coupling and randomization strategy under the worst-case LLM next-token distribution that satisfies a min-entropy constraint. We provide a closed-form expression of the resulting detection rate under the proposed scheme and quantify the cost in a max-min sense. Finally, we provide an array of numerical results, comparing the proposed scheme with the theoretical optimum and existing schemes, in both synthetic data and LLM watermarking. Our code is available at https://github.com/Carol-Long/CC_Watermark
Soft Best-of-n Sampling for Model Alignment
May 06, 2025Abstract:Best-of-$n$ (BoN) sampling is a practical approach for aligning language model outputs with human preferences without expensive fine-tuning. BoN sampling is performed by generating $n$ responses to a prompt and then selecting the sample that maximizes a reward function. BoN yields high reward values in practice at a distortion cost, as measured by the KL-divergence between the sampled and original distribution. This distortion is coarsely controlled by varying the number of samples: larger $n$ yields a higher reward at a higher distortion cost. We introduce Soft Best-of-$n$ sampling, a generalization of BoN that allows for smooth interpolation between the original distribution and reward-maximizing distribution through a temperature parameter $\lambda$. We establish theoretical guarantees showing that Soft Best-of-$n$ sampling converges sharply to the optimal tilted distribution at a rate of $O(1/n)$ in KL and the expected (relative) reward. For sequences of discrete outputs, we analyze an additive reward model that reveals the fundamental limitations of blockwise sampling.
Measuring Progress in Dictionary Learning for Language Model Interpretability with Board Game Models
Jul 31, 2024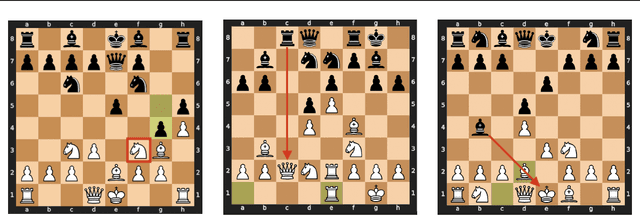
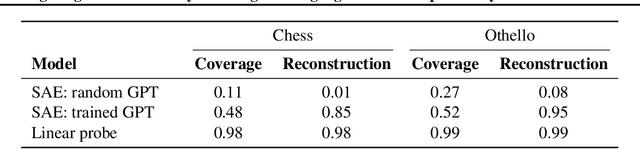
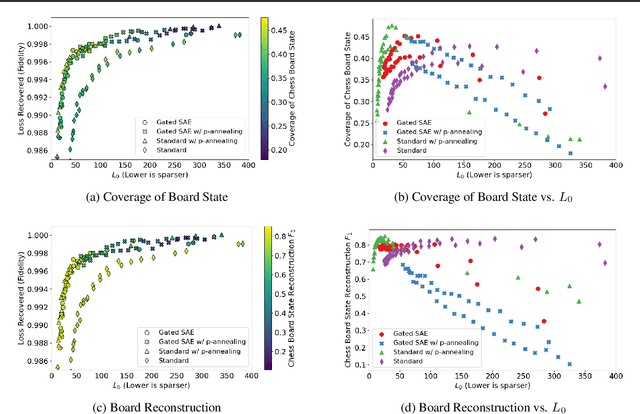
Abstract:What latent features are encoded in language model (LM) representations? Recent work on training sparse autoencoders (SAEs) to disentangle interpretable features in LM representations has shown significant promise. However, evaluating the quality of these SAEs is difficult because we lack a ground-truth collection of interpretable features that we expect good SAEs to recover. We thus propose to measure progress in interpretable dictionary learning by working in the setting of LMs trained on chess and Othello transcripts. These settings carry natural collections of interpretable features -- for example, "there is a knight on F3" -- which we leverage into $\textit{supervised}$ metrics for SAE quality. To guide progress in interpretable dictionary learning, we introduce a new SAE training technique, $\textit{p-annealing}$, which improves performance on prior unsupervised metrics as well as our new metrics.
Non-Asymptotic Uncertainty Quantification in High-Dimensional Learning
Jul 18, 2024
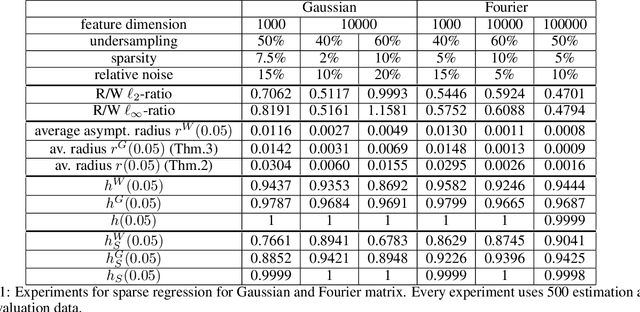

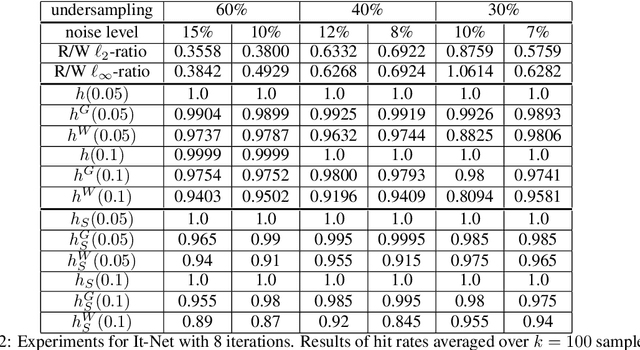
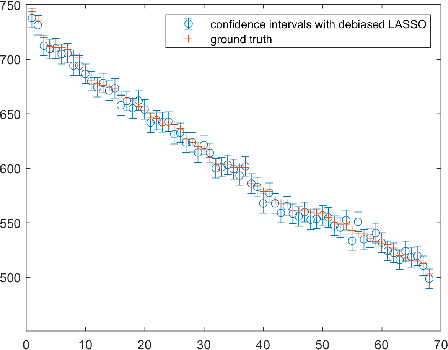
Abstract:Uncertainty quantification (UQ) is a crucial but challenging task in many high-dimensional regression or learning problems to increase the confidence of a given predictor. We develop a new data-driven approach for UQ in regression that applies both to classical regression approaches such as the LASSO as well as to neural networks. One of the most notable UQ techniques is the debiased LASSO, which modifies the LASSO to allow for the construction of asymptotic confidence intervals by decomposing the estimation error into a Gaussian and an asymptotically vanishing bias component. However, in real-world problems with finite-dimensional data, the bias term is often too significant to be neglected, resulting in overly narrow confidence intervals. Our work rigorously addresses this issue and derives a data-driven adjustment that corrects the confidence intervals for a large class of predictors by estimating the means and variances of the bias terms from training data, exploiting high-dimensional concentration phenomena. This gives rise to non-asymptotic confidence intervals, which can help avoid overestimating uncertainty in critical applications such as MRI diagnosis. Importantly, our analysis extends beyond sparse regression to data-driven predictors like neural networks, enhancing the reliability of model-based deep learning. Our findings bridge the gap between established theory and the practical applicability of such debiased methods.
High-Dimensional Confidence Regions in Sparse MRI
Jul 18, 2024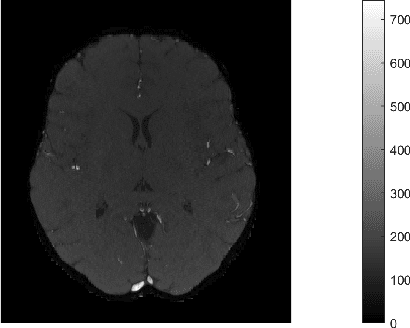
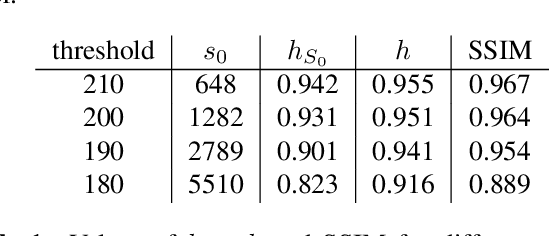
Abstract:One of the most promising solutions for uncertainty quantification in high-dimensional statistics is the debiased LASSO that relies on unconstrained $\ell_1$-minimization. The initial works focused on real Gaussian designs as a toy model for this problem. However, in medical imaging applications, such as compressive sensing for MRI, the measurement system is represented by a (subsampled) complex Fourier matrix. The purpose of this work is to extend the method to the MRI case in order to construct confidence intervals for each pixel of an MR image. We show that a sufficient amount of data is $n \gtrsim \max\{ s_0\log^2 s_0\log p, s_0 \log^2 p \}$.
With or Without Replacement? Improving Confidence in Fourier Imaging
Jul 18, 2024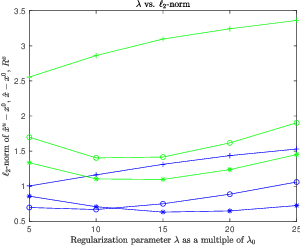
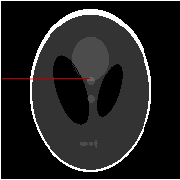
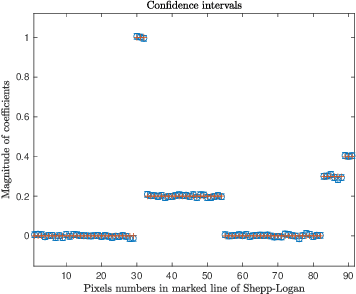
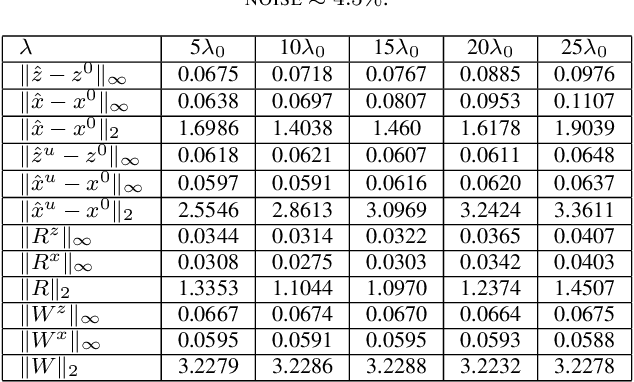
Abstract:Over the last few years, debiased estimators have been proposed in order to establish rigorous confidence intervals for high-dimensional problems in machine learning and data science. The core argument is that the error of these estimators with respect to the ground truth can be expressed as a Gaussian variable plus a remainder term that vanishes as long as the dimension of the problem is sufficiently high. Thus, uncertainty quantification (UQ) can be performed exploiting the Gaussian model. Empirically, however, the remainder term cannot be neglected in many realistic situations of moderately-sized dimensions, in particular in certain structured measurement scenarios such as Magnetic Resonance Imaging (MRI). This, in turn, can downgrade the advantage of the UQ methods as compared to non-UQ approaches such as the standard LASSO. In this paper, we present a method to improve the debiased estimator by sampling without replacement. Our approach leverages recent results of ours on the structure of the random nature of certain sampling schemes showing how a transition between sampling with and without replacement can lead to a weighted reconstruction scheme with improved performance for the standard LASSO. In this paper, we illustrate how this reweighted sampling idea can also improve the debiased estimator and, consequently, provide a better method for UQ in Fourier imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge