Solving Inverse Problems with Deep Linear Neural Networks: Global Convergence Guarantees for Gradient Descent with Weight Decay

Machine learning methods are commonly used to solve inverse problems, wherein an unknown signal must be estimated from few measurements generated via a known acquisition procedure. In particular, neural networks perform well empirically but have limited theoretical guarantees. In this work, we study an underdetermined linear inverse problem that admits several possible solution mappings. A standard remedy (e.g., in compressed sensing) establishing uniqueness of the solution mapping is to assume knowledge of latent low-dimensional structure in the source signal. We ask the following question: do deep neural networks adapt to this low-dimensional structure when trained by gradient descent with weight decay regularization? We prove that mildly overparameterized deep linear networks trained in this manner converge to an approximate solution that accurately solves the inverse problem while implicitly encoding latent subspace structure. To our knowledge, this is the first result to rigorously show that deep linear networks trained with weight decay automatically adapt to latent subspace structure in the data under practical stepsize and weight initialization schemes. Our work highlights that regularization and overparameterization improve generalization, while overparameterization also accelerates convergence during training.

Non-Asymptotic Uncertainty Quantification in High-Dimensional Learning

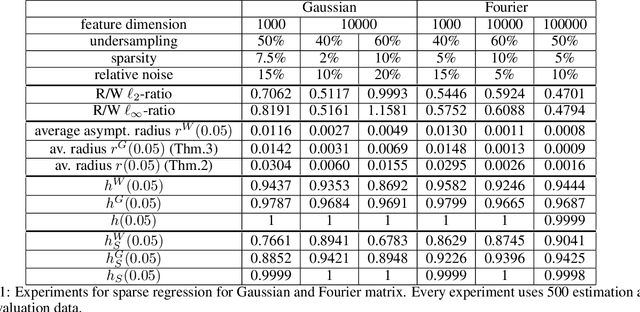
Uncertainty quantification (UQ) is a crucial but challenging task in many high-dimensional regression or learning problems to increase the confidence of a given predictor. We develop a new data-driven approach for UQ in regression that applies both to classical regression approaches such as the LASSO as well as to neural networks. One of the most notable UQ techniques is the debiased LASSO, which modifies the LASSO to allow for the construction of asymptotic confidence intervals by decomposing the estimation error into a Gaussian and an asymptotically vanishing bias component. However, in real-world problems with finite-dimensional data, the bias term is often too significant to be neglected, resulting in overly narrow confidence intervals. Our work rigorously addresses this issue and derives a data-driven adjustment that corrects the confidence intervals for a large class of predictors by estimating the means and variances of the bias terms from training data, exploiting high-dimensional concentration phenomena. This gives rise to non-asymptotic confidence intervals, which can help avoid overestimating uncertainty in critical applications such as MRI diagnosis. Importantly, our analysis extends beyond sparse regression to data-driven predictors like neural networks, enhancing the reliability of model-based deep learning. Our findings bridge the gap between established theory and the practical applicability of such debiased methods.

Uncertainty quantification for learned ISTA

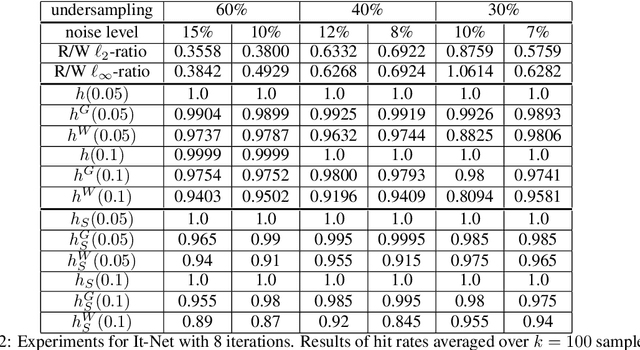
Model-based deep learning solutions to inverse problems have attracted increasing attention in recent years as they bridge state-of-the-art numerical performance with interpretability. In addition, the incorporated prior domain knowledge can make the training more efficient as the smaller number of parameters allows the training step to be executed with smaller datasets. Algorithm unrolling schemes stand out among these model-based learning techniques. Despite their rapid advancement and their close connection to traditional high-dimensional statistical methods, they lack certainty estimates and a theory for uncertainty quantification is still elusive. This work provides a step towards closing this gap proposing a rigorous way to obtain confidence intervals for the LISTA estimator.