Solving Inverse Problems with Deep Linear Neural Networks: Global Convergence Guarantees for Gradient Descent with Weight Decay

Machine learning methods are commonly used to solve inverse problems, wherein an unknown signal must be estimated from few measurements generated via a known acquisition procedure. In particular, neural networks perform well empirically but have limited theoretical guarantees. In this work, we study an underdetermined linear inverse problem that admits several possible solution mappings. A standard remedy (e.g., in compressed sensing) establishing uniqueness of the solution mapping is to assume knowledge of latent low-dimensional structure in the source signal. We ask the following question: do deep neural networks adapt to this low-dimensional structure when trained by gradient descent with weight decay regularization? We prove that mildly overparameterized deep linear networks trained in this manner converge to an approximate solution that accurately solves the inverse problem while implicitly encoding latent subspace structure. To our knowledge, this is the first result to rigorously show that deep linear networks trained with weight decay automatically adapt to latent subspace structure in the data under practical stepsize and weight initialization schemes. Our work highlights that regularization and overparameterization improve generalization, while overparameterization also accelerates convergence during training.

Implicit Regularization for Tubal Tensor Factorizations via Gradient Descent

We provide a rigorous analysis of implicit regularization in an overparametrized tensor factorization problem beyond the lazy training regime. For matrix factorization problems, this phenomenon has been studied in a number of works. A particular challenge has been to design universal initialization strategies which provably lead to implicit regularization in gradient-descent methods. At the same time, it has been argued by Cohen et. al. 2016 that more general classes of neural networks can be captured by considering tensor factorizations. However, in the tensor case, implicit regularization has only been rigorously established for gradient flow or in the lazy training regime. In this paper, we prove the first tensor result of its kind for gradient descent rather than gradient flow. We focus on the tubal tensor product and the associated notion of low tubal rank, encouraged by the relevance of this model for image data. We establish that gradient descent in an overparametrized tensor factorization model with a small random initialization exhibits an implicit bias towards solutions of low tubal rank. Our theoretical findings are illustrated in an extensive set of numerical simulations show-casing the dynamics predicted by our theory as well as the crucial role of using a small random initialization.

Non-Asymptotic Uncertainty Quantification in High-Dimensional Learning

Uncertainty quantification (UQ) is a crucial but challenging task in many high-dimensional regression or learning problems to increase the confidence of a given predictor. We develop a new data-driven approach for UQ in regression that applies both to classical regression approaches such as the LASSO as well as to neural networks. One of the most notable UQ techniques is the debiased LASSO, which modifies the LASSO to allow for the construction of asymptotic confidence intervals by decomposing the estimation error into a Gaussian and an asymptotically vanishing bias component. However, in real-world problems with finite-dimensional data, the bias term is often too significant to be neglected, resulting in overly narrow confidence intervals. Our work rigorously addresses this issue and derives a data-driven adjustment that corrects the confidence intervals for a large class of predictors by estimating the means and variances of the bias terms from training data, exploiting high-dimensional concentration phenomena. This gives rise to non-asymptotic confidence intervals, which can help avoid overestimating uncertainty in critical applications such as MRI diagnosis. Importantly, our analysis extends beyond sparse regression to data-driven predictors like neural networks, enhancing the reliability of model-based deep learning. Our findings bridge the gap between established theory and the practical applicability of such debiased methods.

High-Dimensional Confidence Regions in Sparse MRI

One of the most promising solutions for uncertainty quantification in high-dimensional statistics is the debiased LASSO that relies on unconstrained $\ell_1$-minimization. The initial works focused on real Gaussian designs as a toy model for this problem. However, in medical imaging applications, such as compressive sensing for MRI, the measurement system is represented by a (subsampled) complex Fourier matrix. The purpose of this work is to extend the method to the MRI case in order to construct confidence intervals for each pixel of an MR image. We show that a sufficient amount of data is $n \gtrsim \max\{ s_0\log^2 s_0\log p, s_0 \log^2 p \}$.

With or Without Replacement? Improving Confidence in Fourier Imaging

Over the last few years, debiased estimators have been proposed in order to establish rigorous confidence intervals for high-dimensional problems in machine learning and data science. The core argument is that the error of these estimators with respect to the ground truth can be expressed as a Gaussian variable plus a remainder term that vanishes as long as the dimension of the problem is sufficiently high. Thus, uncertainty quantification (UQ) can be performed exploiting the Gaussian model. Empirically, however, the remainder term cannot be neglected in many realistic situations of moderately-sized dimensions, in particular in certain structured measurement scenarios such as Magnetic Resonance Imaging (MRI). This, in turn, can downgrade the advantage of the UQ methods as compared to non-UQ approaches such as the standard LASSO. In this paper, we present a method to improve the debiased estimator by sampling without replacement. Our approach leverages recent results of ours on the structure of the random nature of certain sampling schemes showing how a transition between sampling with and without replacement can lead to a weighted reconstruction scheme with improved performance for the standard LASSO. In this paper, we illustrate how this reweighted sampling idea can also improve the debiased estimator and, consequently, provide a better method for UQ in Fourier imaging.

The Mathematics of Dots and Pixels: On the Theoretical Foundations of Image Halftoning

The evolution of image halftoning, from its analog roots to contemporary digital methodologies, encapsulates a fascinating journey marked by technological advancements and creative innovations. Yet the theoretical understanding of halftoning is much more recent. In this article, we explore various approaches towards shedding light on the design of halftoning approaches and why they work. We discuss both halftoning in a continuous domain and on a pixel grid. We start by reviewing the mathematical foundation of the so-called electrostatic halftoning method, which departed from the heuristic of considering the back dots of the halftoned image as charged particles attracted by the grey values of the image in combination with mutual repulsion. Such an attraction-repulsion model can be mathematically represented via an energy functional in a reproducing kernel Hilbert space allowing for a rigorous analysis of the resulting optimization problem as well as a convergence analysis in a suitable topology. A second class of methods that we discuss in detail is the class of error diffusion schemes, arguably among the most popular halftoning techniques due to their ability to work directly on a pixel grid and their ease of application. The main idea of these schemes is to choose the locations of the black pixels via a recurrence relation designed to agree with the image in terms of the local averages. We discuss some recent mathematical understanding of these methods that is based on a connection to Sigma-Delta quantizers, a popular class of algorithms for analog-to-digital conversion.

Uncertainty quantification for learned ISTA

Model-based deep learning solutions to inverse problems have attracted increasing attention in recent years as they bridge state-of-the-art numerical performance with interpretability. In addition, the incorporated prior domain knowledge can make the training more efficient as the smaller number of parameters allows the training step to be executed with smaller datasets. Algorithm unrolling schemes stand out among these model-based learning techniques. Despite their rapid advancement and their close connection to traditional high-dimensional statistical methods, they lack certainty estimates and a theory for uncertainty quantification is still elusive. This work provides a step towards closing this gap proposing a rigorous way to obtain confidence intervals for the LISTA estimator.

Approximating Positive Homogeneous Functions with Scale Invariant Neural Networks

We investigate to what extent it is possible to solve linear inverse problems with $ReLu$ networks. Due to the scaling invariance arising from the linearity, an optimal reconstruction function $f$ for such a problem is positive homogeneous, i.e., satisfies $f(\lambda x) = \lambda f(x)$ for all non-negative $\lambda$. In a $ReLu$ network, this condition translates to considering networks without bias terms. We first consider recovery of sparse vectors from few linear measurements. We prove that $ReLu$- networks with only one hidden layer cannot even recover $1$-sparse vectors, not even approximately, and regardless of the width of the network. However, with two hidden layers, approximate recovery with arbitrary precision and arbitrary sparsity level $s$ is possible in a stable way. We then extend our results to a wider class of recovery problems including low-rank matrix recovery and phase retrieval. Furthermore, we also consider the approximation of general positive homogeneous functions with neural networks. Extending previous work, we establish new results explaining under which conditions such functions can be approximated with neural networks. Our results also shed some light on the seeming contradiction between previous works showing that neural networks for inverse problems typically have very large Lipschitz constants, but still perform very well also for adversarial noise. Namely, the error bounds in our expressivity results include a combination of a small constant term and a term that is linear in the noise level, indicating that robustness issues may occur only for very small noise levels.

How robust is randomized blind deconvolution via nuclear norm minimization against adversarial noise?

In this paper, we study the problem of recovering two unknown signals from their convolution, which is commonly referred to as blind deconvolution. Reformulation of blind deconvolution as a low-rank recovery problem has led to multiple theoretical recovery guarantees in the past decade due to the success of the nuclear norm minimization heuristic. In particular, in the absence of noise, exact recovery has been established for sufficiently incoherent signals contained in lower-dimensional subspaces. However, if the convolution is corrupted by additive bounded noise, the stability of the recovery problem remains much less understood. In particular, existing reconstruction bounds involve large dimension factors and therefore fail to explain the empirical evidence for dimension-independent robustness of nuclear norm minimization. Recently, theoretical evidence has emerged for ill-posed behavior of low-rank matrix recovery for sufficiently small noise levels. In this work, we develop improved recovery guarantees for blind deconvolution with adversarial noise which exhibit square-root scaling in the noise level. Hence, our results are consistent with existing counterexamples which speak against linear scaling in the noise level as demonstrated for related low-rank matrix recovery problems.

Non-intrusive surrogate modelling using sparse random features with applications in crashworthiness analysis

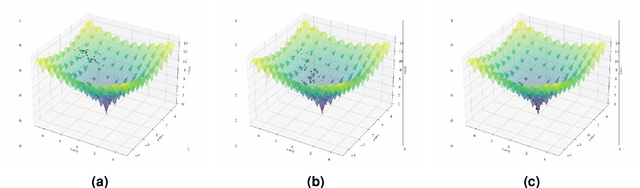
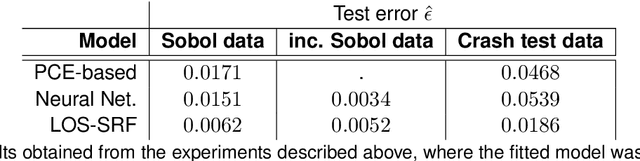
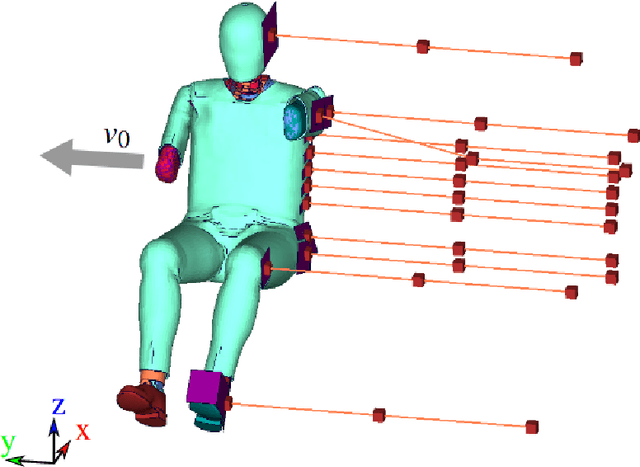
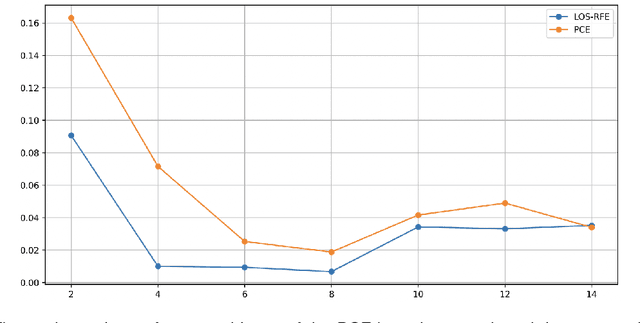
Efficient surrogate modelling is a key requirement for uncertainty quantification in data-driven scenarios. In this work, a novel approach of using Sparse Random Features for surrogate modelling in combination with self-supervised dimensionality reduction is described. The method is compared to other methods on synthetic and real data obtained from crashworthiness analyses. The results show a superiority of the here described approach over state of the art surrogate modelling techniques, Polynomial Chaos Expansions and Neural Networks.