Implicit Regularization for Tubal Tensor Factorizations via Gradient Descent

We provide a rigorous analysis of implicit regularization in an overparametrized tensor factorization problem beyond the lazy training regime. For matrix factorization problems, this phenomenon has been studied in a number of works. A particular challenge has been to design universal initialization strategies which provably lead to implicit regularization in gradient-descent methods. At the same time, it has been argued by Cohen et. al. 2016 that more general classes of neural networks can be captured by considering tensor factorizations. However, in the tensor case, implicit regularization has only been rigorously established for gradient flow or in the lazy training regime. In this paper, we prove the first tensor result of its kind for gradient descent rather than gradient flow. We focus on the tubal tensor product and the associated notion of low tubal rank, encouraged by the relevance of this model for image data. We establish that gradient descent in an overparametrized tensor factorization model with a small random initialization exhibits an implicit bias towards solutions of low tubal rank. Our theoretical findings are illustrated in an extensive set of numerical simulations show-casing the dynamics predicted by our theory as well as the crucial role of using a small random initialization.

The Mathematics of Dots and Pixels: On the Theoretical Foundations of Image Halftoning

The evolution of image halftoning, from its analog roots to contemporary digital methodologies, encapsulates a fascinating journey marked by technological advancements and creative innovations. Yet the theoretical understanding of halftoning is much more recent. In this article, we explore various approaches towards shedding light on the design of halftoning approaches and why they work. We discuss both halftoning in a continuous domain and on a pixel grid. We start by reviewing the mathematical foundation of the so-called electrostatic halftoning method, which departed from the heuristic of considering the back dots of the halftoned image as charged particles attracted by the grey values of the image in combination with mutual repulsion. Such an attraction-repulsion model can be mathematically represented via an energy functional in a reproducing kernel Hilbert space allowing for a rigorous analysis of the resulting optimization problem as well as a convergence analysis in a suitable topology. A second class of methods that we discuss in detail is the class of error diffusion schemes, arguably among the most popular halftoning techniques due to their ability to work directly on a pixel grid and their ease of application. The main idea of these schemes is to choose the locations of the black pixels via a recurrence relation designed to agree with the image in terms of the local averages. We discuss some recent mathematical understanding of these methods that is based on a connection to Sigma-Delta quantizers, a popular class of algorithms for analog-to-digital conversion.

Regularized Shannon sampling formulas related to the special affine Fourier transform

In this paper, we present new regularized Shannon sampling formulas related to the special affine Fourier transform (SAFT). These sampling formulas use localized sampling with special compactly supported window functions, namely B-spline, sinh-type, and continuous Kaiser-Bessel window functions. In contrast to the Shannon sampling series for SAFT, the regularized Shannon sampling formulas for SAFT possesses an exponential decay of the approximation error and are numerically robust in the presence of noise, if certain oversampling condition is fulfilled. Several numerical experiments illustrate the theoretical results.

Non-intrusive surrogate modelling using sparse random features with applications in crashworthiness analysis

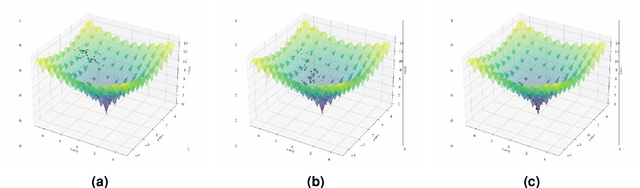
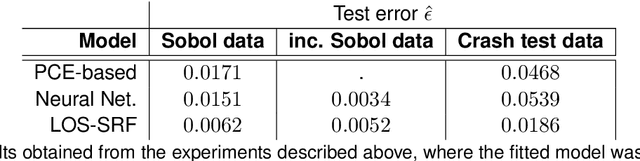
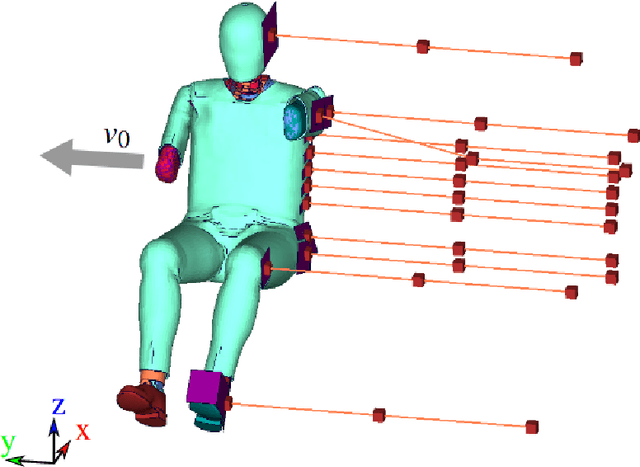
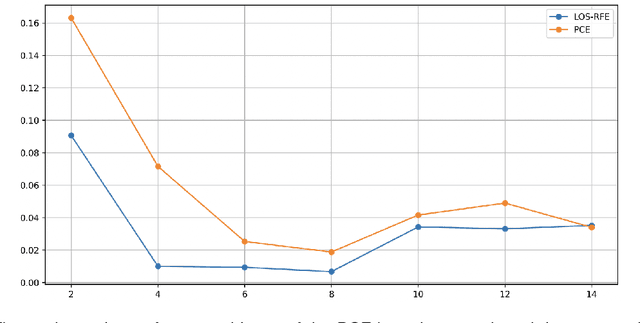
Efficient surrogate modelling is a key requirement for uncertainty quantification in data-driven scenarios. In this work, a novel approach of using Sparse Random Features for surrogate modelling in combination with self-supervised dimensionality reduction is described. The method is compared to other methods on synthetic and real data obtained from crashworthiness analyses. The results show a superiority of the here described approach over state of the art surrogate modelling techniques, Polynomial Chaos Expansions and Neural Networks.