Reliable Evaluation of MRI Motion Correction: Dataset and Insights

Correcting motion artifacts in MRI is important, as they can hinder accurate diagnosis. However, evaluating deep learning-based and classical motion correction methods remains fundamentally difficult due to the lack of accessible ground-truth target data. To address this challenge, we study three evaluation approaches: real-world evaluation based on reference scans, simulated motion, and reference-free evaluation, each with its merits and shortcomings. To enable evaluation with real-world motion artifacts, we release PMoC3D, a dataset consisting of unprocessed Paired Motion-Corrupted 3D brain MRI data. To advance evaluation quality, we introduce MoMRISim, a feature-space metric trained for evaluating motion reconstructions. We assess each evaluation approach and find real-world evaluation together with MoMRISim, while not perfect, to be most reliable. Evaluation based on simulated motion systematically exaggerates algorithm performance, and reference-free evaluation overrates oversmoothed deep learning outputs.

OpenThoughts: Data Recipes for Reasoning Models

Reasoning models have made rapid progress on many benchmarks involving math, code, and science. Yet, there are still many open questions about the best training recipes for reasoning since state-of-the-art models often rely on proprietary datasets with little to no public information available. To address this, the goal of the OpenThoughts project is to create open-source datasets for training reasoning models. After initial explorations, our OpenThoughts2-1M dataset led to OpenThinker2-32B, the first model trained on public reasoning data to match DeepSeek-R1-Distill-32B on standard reasoning benchmarks such as AIME and LiveCodeBench. We then improve our dataset further by systematically investigating each step of our data generation pipeline with 1,000+ controlled experiments, which led to OpenThoughts3. Scaling the pipeline to 1.2M examples and using QwQ-32B as teacher yields our OpenThoughts3-7B model, which achieves state-of-the-art results: 53% on AIME 2025, 51% on LiveCodeBench 06/24-01/25, and 54% on GPQA Diamond - improvements of 15.3, 17.2, and 20.5 percentage points compared to the DeepSeek-R1-Distill-Qwen-7B. All of our datasets and models are available on https://openthoughts.ai.

Efficient Noise Calculation in Deep Learning-based MRI Reconstructions

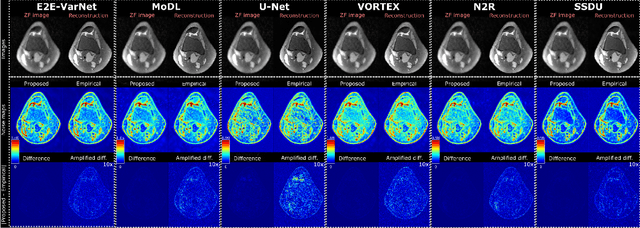
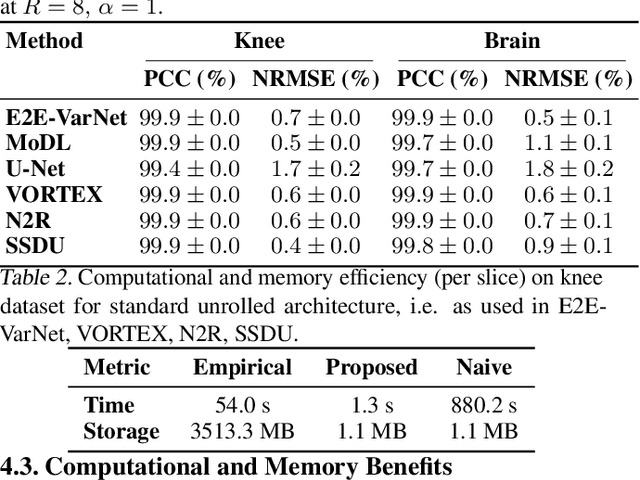
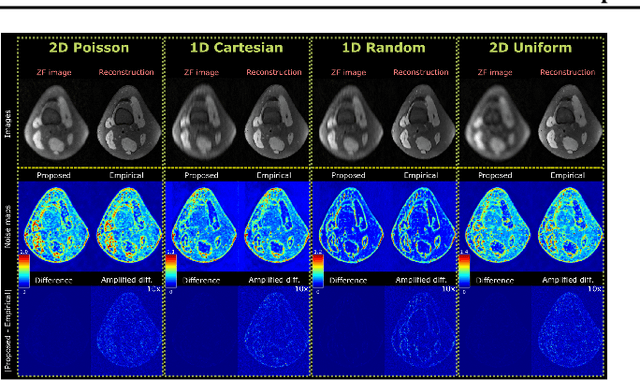
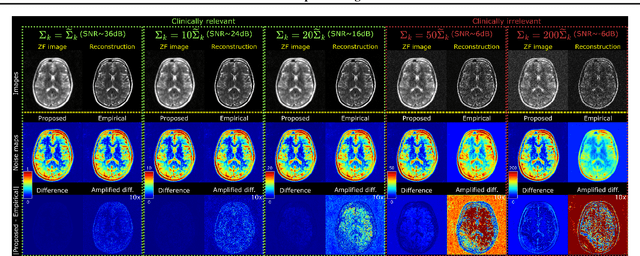
Accelerated MRI reconstruction involves solving an ill-posed inverse problem where noise in acquired data propagates to the reconstructed images. Noise analyses are central to MRI reconstruction for providing an explicit measure of solution fidelity and for guiding the design and deployment of novel reconstruction methods. However, deep learning (DL)-based reconstruction methods have often overlooked noise propagation due to inherent analytical and computational challenges, despite its critical importance. This work proposes a theoretically grounded, memory-efficient technique to calculate voxel-wise variance for quantifying uncertainty due to acquisition noise in accelerated MRI reconstructions. Our approach approximates noise covariance using the DL network's Jacobian, which is intractable to calculate. To circumvent this, we derive an unbiased estimator for the diagonal of this covariance matrix (voxel-wise variance) and introduce a Jacobian sketching technique to efficiently implement it. We evaluate our method on knee and brain MRI datasets for both data- and physics-driven networks trained in supervised and unsupervised manners. Compared to empirical references obtained via Monte Carlo simulations, our technique achieves near-equivalent performance while reducing computational and memory demands by an order of magnitude or more. Furthermore, our method is robust across varying input noise levels, acceleration factors, and diverse undersampling schemes, highlighting its broad applicability. Our work reintroduces accurate and efficient noise analysis as a central tenet of reconstruction algorithms, holding promise to reshape how we evaluate and deploy DL-based MRI. Our code will be made publicly available upon acceptance.

LLM-Guided Search for Deletion-Correcting Codes

Finding deletion-correcting codes of maximum size has been an open problem for over 70 years, even for a single deletion. In this paper, we propose a novel approach for constructing deletion-correcting codes. A code is a set of sequences satisfying certain constraints, and we construct it by greedily adding the highest-priority sequence according to a priority function. To find good priority functions, we leverage FunSearch, a large language model (LLM)-guided evolutionary search proposed by Romera et al., 2024. FunSearch iteratively generates, evaluates, and refines priority functions to construct large deletion-correcting codes. For a single deletion, our evolutionary search finds functions that construct codes which match known maximum sizes, reach the size of the largest (conjectured optimal) Varshamov-Tenengolts codes where the maximum is unknown, and independently rediscover them in equivalent form. For two deletions, we find functions that construct codes with new best-known sizes for code lengths \( n = 12, 13 \), and \( 16 \), establishing improved lower bounds. These results demonstrate the potential of LLM-guided search for information theory and code design and represent the first application of such methods for constructing error-correcting codes.

Resolution-Robust 3D MRI Reconstruction with 2D Diffusion Priors: Diverse-Resolution Training Outperforms Interpolation

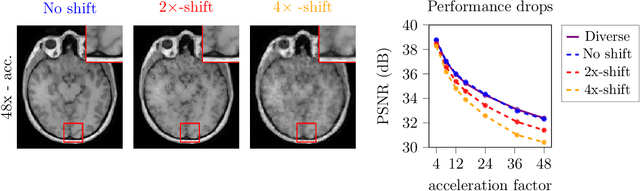
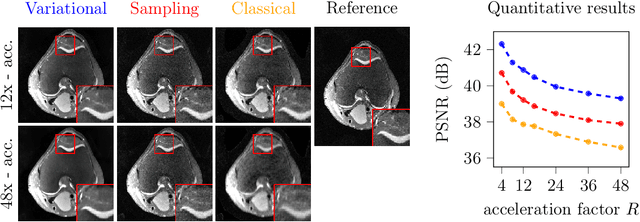
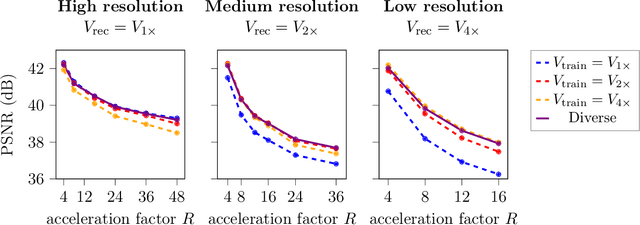
Deep learning-based 3D imaging, in particular magnetic resonance imaging (MRI), is challenging because of limited availability of 3D training data. Therefore, 2D diffusion models trained on 2D slices are starting to be leveraged for 3D MRI reconstruction. However, as we show in this paper, existing methods pertain to a fixed voxel size, and performance degrades when the voxel size is varied, as it is often the case in clinical practice. In this paper, we propose and study several approaches for resolution-robust 3D MRI reconstruction with 2D diffusion priors. As a result of this investigation, we obtain a simple resolution-robust variational 3D reconstruction approach based on diffusion-guided regularization of randomly sampled 2D slices. This method provides competitive reconstruction quality compared to posterior sampling baselines. Towards resolving the sensitivity to resolution-shifts, we investigate state-of-the-art model-based approaches including Gaussian splatting, neural representations, and infinite-dimensional diffusion models, as well as a simple data-centric approach of training the diffusion model on several resolutions. Our experiments demonstrate that the model-based approaches fail to close the performance gap in 3D MRI. In contrast, the data-centric approach of training the diffusion model on various resolutions effectively provides a resolution-robust method without compromising accuracy.

Measuring Bias of Web-filtered Text Datasets and Bias Propagation Through Training

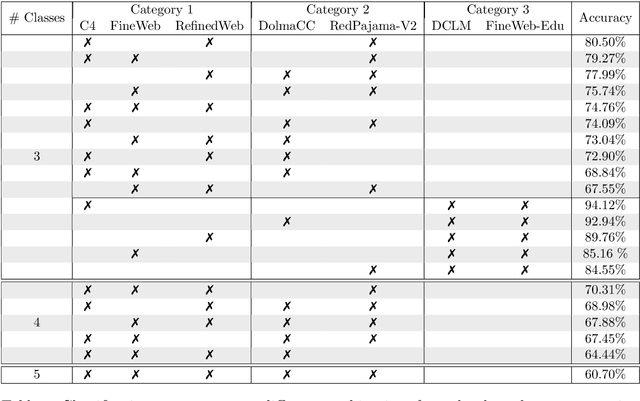
We investigate biases in pretraining datasets for large language models (LLMs) through dataset classification experiments. Building on prior work demonstrating the existence of biases in popular computer vision datasets, we analyze popular open-source pretraining datasets for LLMs derived from CommonCrawl including C4, RefinedWeb, DolmaCC, RedPajama-V2, FineWeb, and DCLM-Baseline. Despite those datasets being obtained with similar filtering and deduplication steps, neural networks can classify surprisingly well which dataset a single text sequence belongs to, significantly better than a human can. This indicates that popular pretraining datasets have their own unique biases or fingerprints. Those biases remain even when the text is rewritten with LLMs. Moreover, these biases propagate through training: Random sequences generated by models trained on those datasets can be classified well by a classifier trained on the original datasets.

MotionTTT: 2D Test-Time-Training Motion Estimation for 3D Motion Corrected MRI

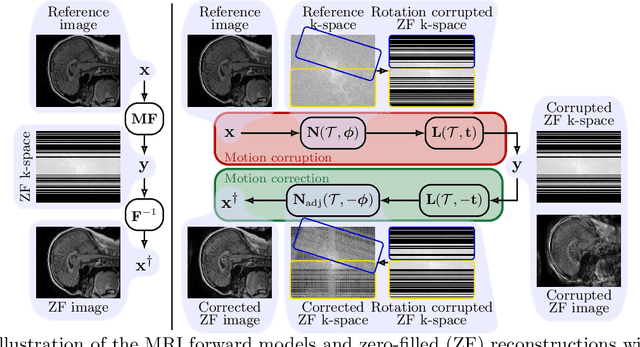
A major challenge of the long measurement times in magnetic resonance imaging (MRI), an important medical imaging technology, is that patients may move during data acquisition. This leads to severe motion artifacts in the reconstructed images and volumes. In this paper, we propose a deep learning-based test-time-training method for accurate motion estimation. The key idea is that a neural network trained for motion-free reconstruction has a small loss if there is no motion, thus optimizing over motion parameters passed through the reconstruction network enables accurate estimation of motion. The estimated motion parameters enable to correct for the motion and to reconstruct accurate motion-corrected images. Our method uses 2D reconstruction networks to estimate rigid motion in 3D, and constitutes the first deep learning based method for 3D rigid motion estimation towards 3D-motion-corrected MRI. We show that our method can provably reconstruct motion parameters for a simple signal and neural network model. We demonstrate the effectiveness of our method for both retrospectively simulated motion and prospectively collected real motion-corrupted data.

DataComp-LM: In search of the next generation of training sets for language models

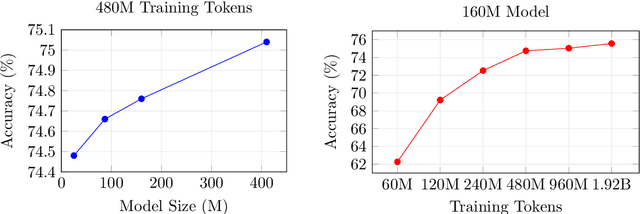
We introduce DataComp for Language Models (DCLM), a testbed for controlled dataset experiments with the goal of improving language models. As part of DCLM, we provide a standardized corpus of 240T tokens extracted from Common Crawl, effective pretraining recipes based on the OpenLM framework, and a broad suite of 53 downstream evaluations. Participants in the DCLM benchmark can experiment with data curation strategies such as deduplication, filtering, and data mixing at model scales ranging from 412M to 7B parameters. As a baseline for DCLM, we conduct extensive experiments and find that model-based filtering is key to assembling a high-quality training set. The resulting dataset, DCLM-Baseline enables training a 7B parameter language model from scratch to 64% 5-shot accuracy on MMLU with 2.6T training tokens. Compared to MAP-Neo, the previous state-of-the-art in open-data language models, DCLM-Baseline represents a 6.6 percentage point improvement on MMLU while being trained with 40% less compute. Our baseline model is also comparable to Mistral-7B-v0.3 and Llama 3 8B on MMLU (63% & 66%), and performs similarly on an average of 53 natural language understanding tasks while being trained with 6.6x less compute than Llama 3 8B. Our results highlight the importance of dataset design for training language models and offer a starting point for further research on data curation.

Deep Learning for Accelerated and Robust MRI Reconstruction: a Review

Deep learning (DL) has recently emerged as a pivotal technology for enhancing magnetic resonance imaging (MRI), a critical tool in diagnostic radiology. This review paper provides a comprehensive overview of recent advances in DL for MRI reconstruction. It focuses on DL approaches and architectures designed to improve image quality, accelerate scans, and address data-related challenges. These include end-to-end neural networks, pre-trained networks, generative models, and self-supervised methods. The paper also discusses the role of DL in optimizing acquisition protocols, enhancing robustness against distribution shifts, and tackling subtle bias. Drawing on the extensive literature and practical insights, it outlines current successes, limitations, and future directions for leveraging DL in MRI reconstruction, while emphasizing the potential of DL to significantly impact clinical imaging practices.

GAMA-IR: Global Additive Multidimensional Averaging for Fast Image Restoration

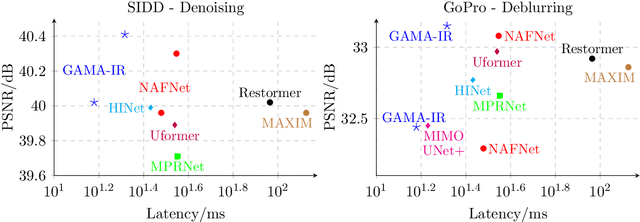
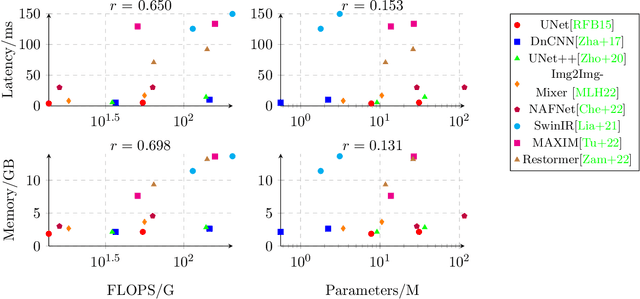
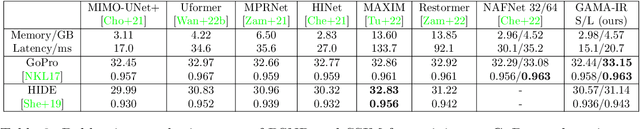
Deep learning-based methods have shown remarkable success for various image restoration tasks such as denoising and deblurring. The current state-of-the-art networks are relatively deep and utilize (variants of) self attention mechanisms. Those networks are significantly slower than shallow convolutional networks, which however perform worse. In this paper, we introduce an image restoration network that is both fast and yields excellent image quality. The network is designed to minimize the latency and memory consumption when executed on a standard GPU, while maintaining state-of-the-art performance. The network is a simple shallow network with an efficient block that implements global additive multidimensional averaging operations. This block can capture global information and enable a large receptive field even when used in shallow networks with minimal computational overhead. Through extensive experiments and evaluations on diverse tasks, we demonstrate that our network achieves comparable or even superior results to existing state-of-the-art image restoration networks with less latency. For instance, we exceed the state-of-the-art result on real-world SIDD denoising by 0.11dB, while being 2 to 10 times faster.