OpenThoughts: Data Recipes for Reasoning Models

Reasoning models have made rapid progress on many benchmarks involving math, code, and science. Yet, there are still many open questions about the best training recipes for reasoning since state-of-the-art models often rely on proprietary datasets with little to no public information available. To address this, the goal of the OpenThoughts project is to create open-source datasets for training reasoning models. After initial explorations, our OpenThoughts2-1M dataset led to OpenThinker2-32B, the first model trained on public reasoning data to match DeepSeek-R1-Distill-32B on standard reasoning benchmarks such as AIME and LiveCodeBench. We then improve our dataset further by systematically investigating each step of our data generation pipeline with 1,000+ controlled experiments, which led to OpenThoughts3. Scaling the pipeline to 1.2M examples and using QwQ-32B as teacher yields our OpenThoughts3-7B model, which achieves state-of-the-art results: 53% on AIME 2025, 51% on LiveCodeBench 06/24-01/25, and 54% on GPQA Diamond - improvements of 15.3, 17.2, and 20.5 percentage points compared to the DeepSeek-R1-Distill-Qwen-7B. All of our datasets and models are available on https://openthoughts.ai.

Synthetic Document Question Answering in Hungarian

Modern VLMs have achieved near-saturation accuracy in English document visual question-answering (VQA). However, this task remains challenging in lower resource languages due to a dearth of suitable training and evaluation data. In this paper we present scalable methods for curating such datasets by focusing on Hungarian, approximately the 17th highest resource language on the internet. Specifically, we present HuDocVQA and HuDocVQA-manual, document VQA datasets that modern VLMs significantly underperform on compared to English DocVQA. HuDocVQA-manual is a small manually curated dataset based on Hungarian documents from Common Crawl, while HuDocVQA is a larger synthetically generated VQA data set from the same source. We apply multiple rounds of quality filtering and deduplication to HuDocVQA in order to match human-level quality in this dataset. We also present HuCCPDF, a dataset of 117k pages from Hungarian Common Crawl PDFs along with their transcriptions, which can be used for training a model for Hungarian OCR. To validate the quality of our datasets, we show how finetuning on a mixture of these datasets can improve accuracy on HuDocVQA for Llama 3.2 11B Instruct by +7.2%. Our datasets and code will be released to the public to foster further research in multilingual DocVQA.

BLIP3-KALE: Knowledge Augmented Large-Scale Dense Captions

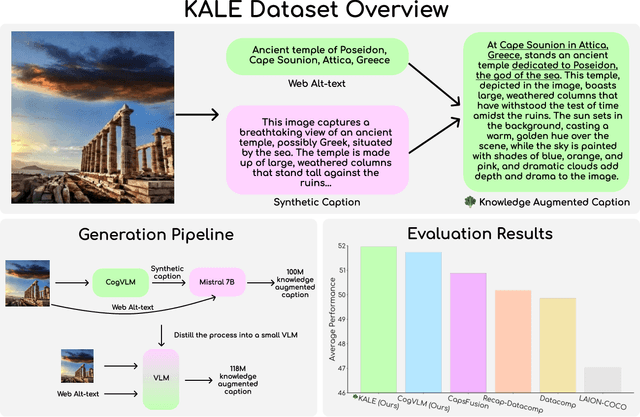
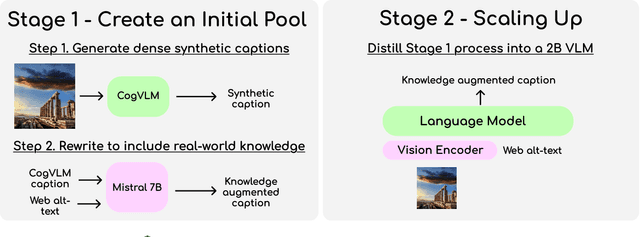
We introduce BLIP3-KALE, a dataset of 218 million image-text pairs that bridges the gap between descriptive synthetic captions and factual web-scale alt-text. KALE augments synthetic dense image captions with web-scale alt-text to generate factually grounded image captions. Our two-stage approach leverages large vision-language models and language models to create knowledge-augmented captions, which are then used to train a specialized VLM for scaling up the dataset. We train vision-language models on KALE and demonstrate improvements on vision-language tasks. Our experiments show the utility of KALE for training more capable and knowledgeable multimodal models. We release the KALE dataset at https://huggingface.co/datasets/Salesforce/blip3-kale

DataComp-LM: In search of the next generation of training sets for language models

We introduce DataComp for Language Models (DCLM), a testbed for controlled dataset experiments with the goal of improving language models. As part of DCLM, we provide a standardized corpus of 240T tokens extracted from Common Crawl, effective pretraining recipes based on the OpenLM framework, and a broad suite of 53 downstream evaluations. Participants in the DCLM benchmark can experiment with data curation strategies such as deduplication, filtering, and data mixing at model scales ranging from 412M to 7B parameters. As a baseline for DCLM, we conduct extensive experiments and find that model-based filtering is key to assembling a high-quality training set. The resulting dataset, DCLM-Baseline enables training a 7B parameter language model from scratch to 64% 5-shot accuracy on MMLU with 2.6T training tokens. Compared to MAP-Neo, the previous state-of-the-art in open-data language models, DCLM-Baseline represents a 6.6 percentage point improvement on MMLU while being trained with 40% less compute. Our baseline model is also comparable to Mistral-7B-v0.3 and Llama 3 8B on MMLU (63% & 66%), and performs similarly on an average of 53 natural language understanding tasks while being trained with 6.6x less compute than Llama 3 8B. Our results highlight the importance of dataset design for training language models and offer a starting point for further research on data curation.

Conformal Prediction via Regression-as-Classification

Conformal prediction (CP) for regression can be challenging, especially when the output distribution is heteroscedastic, multimodal, or skewed. Some of the issues can be addressed by estimating a distribution over the output, but in reality, such approaches can be sensitive to estimation error and yield unstable intervals.~Here, we circumvent the challenges by converting regression to a classification problem and then use CP for classification to obtain CP sets for regression.~To preserve the ordering of the continuous-output space, we design a new loss function and make necessary modifications to the CP classification techniques.~Empirical results on many benchmarks shows that this simple approach gives surprisingly good results on many practical problems.

On the Diminishing Returns of Width for Continual Learning

While deep neural networks have demonstrated groundbreaking performance in various settings, these models often suffer from \emph{catastrophic forgetting} when trained on new tasks in sequence. Several works have empirically demonstrated that increasing the width of a neural network leads to a decrease in catastrophic forgetting but have yet to characterize the exact relationship between width and continual learning. We design one of the first frameworks to analyze Continual Learning Theory and prove that width is directly related to forgetting in Feed-Forward Networks (FFN). Specifically, we demonstrate that increasing network widths to reduce forgetting yields diminishing returns. We empirically verify our claims at widths hitherto unexplored in prior studies where the diminishing returns are clearly observed as predicted by our theory.

On Accelerated Perceptrons and Beyond

The classical Perceptron algorithm of Rosenblatt can be used to find a linear threshold function to correctly classify $n$ linearly separable data points, assuming the classes are separated by some margin $\gamma > 0$. A foundational result is that Perceptron converges after $\Omega(1/\gamma^{2})$ iterations. There have been several recent works that managed to improve this rate by a quadratic factor, to $\Omega(\sqrt{\log n}/\gamma)$, with more sophisticated algorithms. In this paper, we unify these existing results under one framework by showing that they can all be described through the lens of solving min-max problems using modern acceleration techniques, mainly through optimistic online learning. We then show that the proposed framework also lead to improved results for a series of problems beyond the standard Perceptron setting. Specifically, a) For the margin maximization problem, we improve the state-of-the-art result from $O(\log t/t^2)$ to $O(1/t^2)$, where $t$ is the number of iterations; b) We provide the first result on identifying the implicit bias property of the classical Nesterov's accelerated gradient descent (NAG) algorithm, and show NAG can maximize the margin with an $O(1/t^2)$ rate; c) For the classical $p$-norm Perceptron problem, we provide an algorithm with $\Omega(\sqrt{(p-1)\log n}/\gamma)$ convergence rate, while existing algorithms suffer the $\Omega({(p-1)}/\gamma^2)$ convergence rate.