OLMoASR: Open Models and Data for Training Robust Speech Recognition Models

Improvements in training data scale and quality have led to significant advances, yet its influence in speech recognition remains underexplored. In this paper, we present a large-scale dataset, OLMoASR-Pool, and series of models, OLMoASR, to study and develop robust zero-shot speech recognition models. Beginning from OLMoASR-Pool, a collection of 3M hours of English audio and 17M transcripts, we design text heuristic filters to remove low-quality or mistranscribed data. Our curation pipeline produces a new dataset containing 1M hours of high-quality audio-transcript pairs, which we call OLMoASR-Mix. We use OLMoASR-Mix to train the OLMoASR-Mix suite of models, ranging from 39M (tiny.en) to 1.5B (large.en) parameters. Across all model scales, OLMoASR achieves comparable average performance to OpenAI's Whisper on short and long-form speech recognition benchmarks. Notably, OLMoASR-medium.en attains a 12.8\% and 11.0\% word error rate (WER) that is on par with Whisper's largest English-only model Whisper-medium.en's 12.4\% and 10.5\% WER for short and long-form recognition respectively (at equivalent parameter count). OLMoASR-Pool, OLMoASR models, and filtering, training and evaluation code will be made publicly available to further research on robust speech processing.

Datasets, Documents, and Repetitions: The Practicalities of Unequal Data Quality

Data filtering has become a powerful tool for improving model performance while reducing computational cost. However, as large language model compute budgets continue to grow, the limited data volume provided by heavily filtered and deduplicated datasets will become a practical constraint. In efforts to better understand how to proceed, we study model performance at various compute budgets and across multiple pre-training datasets created through data filtering and deduplication. We find that, given appropriate modifications to the training recipe, repeating existing aggressively filtered datasets for up to ten epochs can outperform training on the ten times larger superset for a single epoch across multiple compute budget orders of magnitude. While this finding relies on repeating the dataset for many epochs, we also investigate repeats within these datasets at the document level. We find that not all documents within a dataset are equal, and we can create better datasets relative to a token budget by explicitly manipulating the counts of individual documents. We conclude by arguing that even as large language models scale, data filtering remains an important direction of research.

2 OLMo 2 Furious

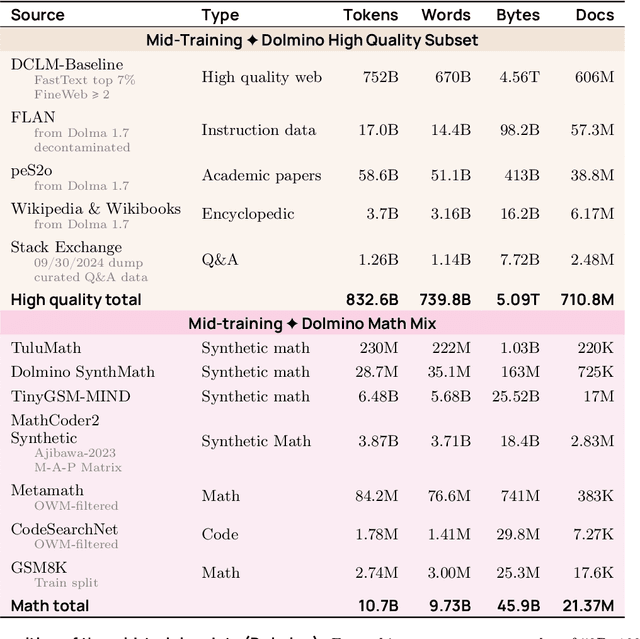
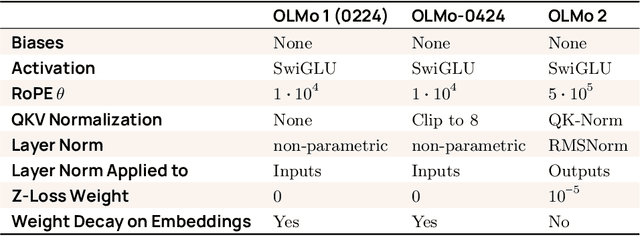
We present OLMo 2, the next generation of our fully open language models. OLMo 2 includes dense autoregressive models with improved architecture and training recipe, pretraining data mixtures, and instruction tuning recipes. Our modified model architecture and training recipe achieve both better training stability and improved per-token efficiency. Our updated pretraining data mixture introduces a new, specialized data mix called Dolmino Mix 1124, which significantly improves model capabilities across many downstream task benchmarks when introduced via late-stage curriculum training (i.e. specialized data during the annealing phase of pretraining). Finally, we incorporate best practices from T\"ulu 3 to develop OLMo 2-Instruct, focusing on permissive data and extending our final-stage reinforcement learning with verifiable rewards (RLVR). Our OLMo 2 base models sit at the Pareto frontier of performance to compute, often matching or outperforming open-weight only models like Llama 3.1 and Qwen 2.5 while using fewer FLOPs and with fully transparent training data, code, and recipe. Our fully open OLMo 2-Instruct models are competitive with or surpassing open-weight only models of comparable size, including Qwen 2.5, Llama 3.1 and Gemma 2. We release all OLMo 2 artifacts openly -- models at 7B and 13B scales, both pretrained and post-trained, including their full training data, training code and recipes, training logs and thousands of intermediate checkpoints. The final instruction model is available on the Ai2 Playground as a free research demo.

DataComp-LM: In search of the next generation of training sets for language models

We introduce DataComp for Language Models (DCLM), a testbed for controlled dataset experiments with the goal of improving language models. As part of DCLM, we provide a standardized corpus of 240T tokens extracted from Common Crawl, effective pretraining recipes based on the OpenLM framework, and a broad suite of 53 downstream evaluations. Participants in the DCLM benchmark can experiment with data curation strategies such as deduplication, filtering, and data mixing at model scales ranging from 412M to 7B parameters. As a baseline for DCLM, we conduct extensive experiments and find that model-based filtering is key to assembling a high-quality training set. The resulting dataset, DCLM-Baseline enables training a 7B parameter language model from scratch to 64% 5-shot accuracy on MMLU with 2.6T training tokens. Compared to MAP-Neo, the previous state-of-the-art in open-data language models, DCLM-Baseline represents a 6.6 percentage point improvement on MMLU while being trained with 40% less compute. Our baseline model is also comparable to Mistral-7B-v0.3 and Llama 3 8B on MMLU (63% & 66%), and performs similarly on an average of 53 natural language understanding tasks while being trained with 6.6x less compute than Llama 3 8B. Our results highlight the importance of dataset design for training language models and offer a starting point for further research on data curation.

MINT-1T: Scaling Open-Source Multimodal Data by 10x: A Multimodal Dataset with One Trillion Tokens

Multimodal interleaved datasets featuring free-form interleaved sequences of images and text are crucial for training frontier large multimodal models (LMMs). Despite the rapid progression of open-source LMMs, there remains a pronounced scarcity of large-scale, diverse open-source multimodal interleaved datasets. In response, we introduce MINT-1T, the most extensive and diverse open-source Multimodal INTerleaved dataset to date. MINT-1T comprises one trillion text tokens and three billion images, a 10x scale-up from existing open-source datasets. Additionally, we include previously untapped sources such as PDFs and ArXiv papers. As scaling multimodal interleaved datasets requires substantial engineering effort, sharing the data curation process and releasing the dataset greatly benefits the community. Our experiments show that LMMs trained on MINT-1T rival the performance of models trained on the previous leading dataset, OBELICS. Our data and code will be released at https://github.com/mlfoundations/MINT-1T.

Conditional Generative Models are Sufficient to Sample from Any Causal Effect Estimand

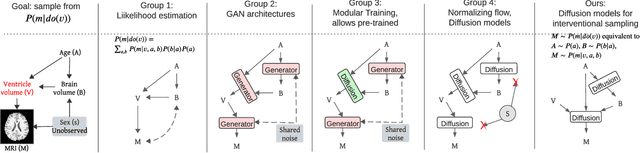
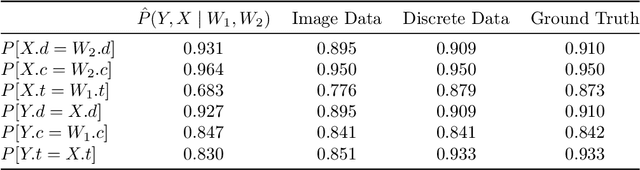
Causal inference from observational data has recently found many applications in machine learning. While sound and complete algorithms exist to compute causal effects, many of these algorithms require explicit access to conditional likelihoods over the observational distribution, which is difficult to estimate in the high-dimensional regime, such as with images. To alleviate this issue, researchers have approached the problem by simulating causal relations with neural models and obtained impressive results. However, none of these existing approaches can be applied to generic scenarios such as causal graphs on image data with latent confounders, or obtain conditional interventional samples. In this paper, we show that any identifiable causal effect given an arbitrary causal graph can be computed through push-forward computations of conditional generative models. Based on this result, we devise a diffusion-based approach to sample from any (conditional) interventional distribution on image data. To showcase our algorithm's performance, we conduct experiments on a Colored MNIST dataset having both the treatment ($X$) and the target variables ($Y$) as images and obtain interventional samples from $P(y|do(x))$. As an application of our algorithm, we evaluate two large conditional generative models that are pre-trained on the CelebA dataset by analyzing the strength of spurious correlations and the level of disentanglement they achieve.

Zonotope Domains for Lagrangian Neural Network Verification

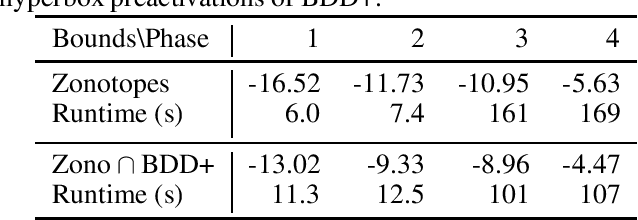
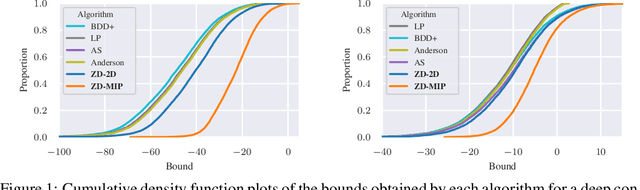
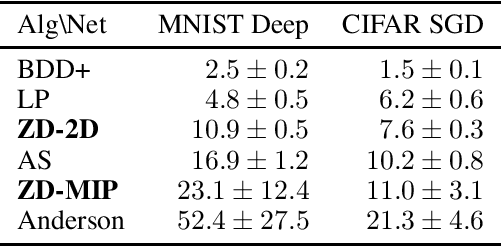
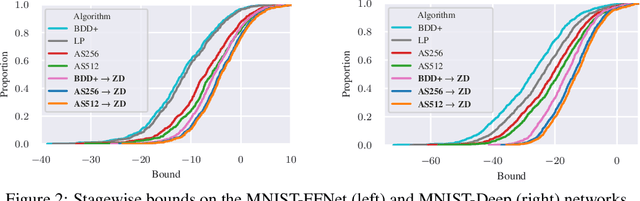
Neural network verification aims to provide provable bounds for the output of a neural network for a given input range. Notable prior works in this domain have either generated bounds using abstract domains, which preserve some dependency between intermediate neurons in the network; or framed verification as an optimization problem and solved a relaxation using Lagrangian methods. A key drawback of the latter technique is that each neuron is treated independently, thereby ignoring important neuron interactions. We provide an approach that merges these two threads and uses zonotopes within a Lagrangian decomposition. Crucially, we can decompose the problem of verifying a deep neural network into the verification of many 2-layer neural networks. While each of these problems is provably hard, we provide efficient relaxation methods that are amenable to efficient dual ascent procedures. Our technique yields bounds that improve upon both linear programming and Lagrangian-based verification techniques in both time and bound tightness.

Inverse Problems Leveraging Pre-trained Contrastive Representations

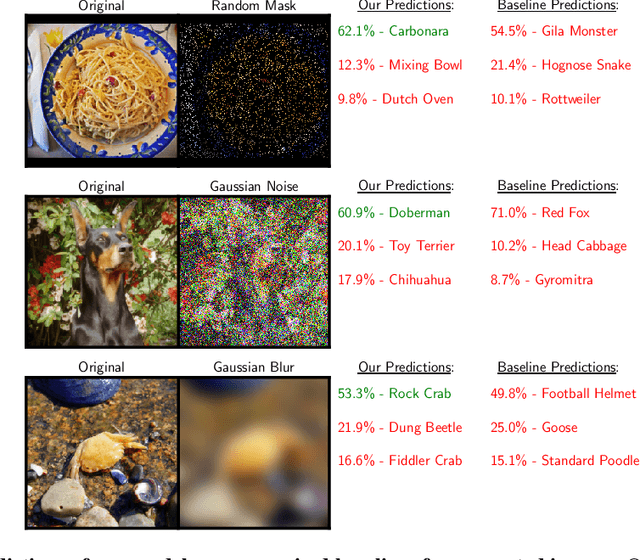
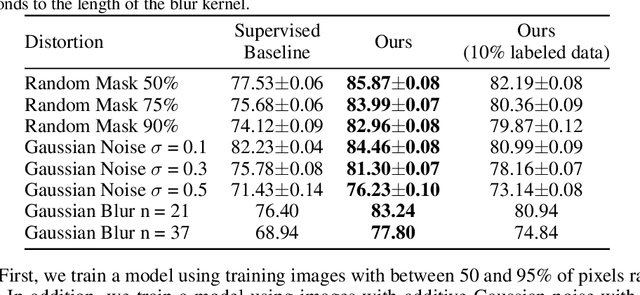
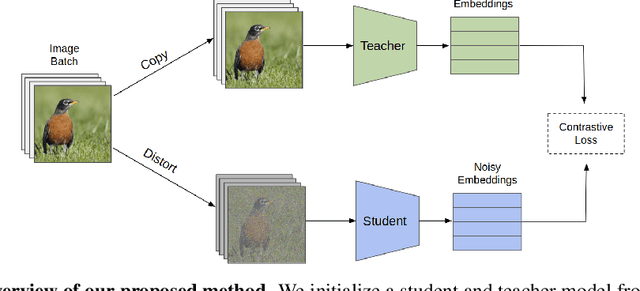
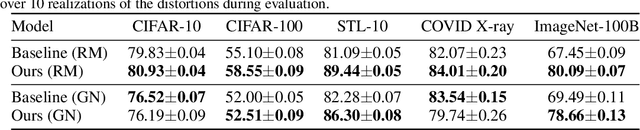
We study a new family of inverse problems for recovering representations of corrupted data. We assume access to a pre-trained representation learning network R(x) that operates on clean images, like CLIP. The problem is to recover the representation of an image R(x), if we are only given a corrupted version A(x), for some known forward operator A. We propose a supervised inversion method that uses a contrastive objective to obtain excellent representations for highly corrupted images. Using a linear probe on our robust representations, we achieve a higher accuracy than end-to-end supervised baselines when classifying images with various types of distortions, including blurring, additive noise, and random pixel masking. We evaluate on a subset of ImageNet and observe that our method is robust to varying levels of distortion. Our method outperforms end-to-end baselines even with a fraction of the labeled data in a wide range of forward operators.

Provable Lipschitz Certification for Generative Models

We present a scalable technique for upper bounding the Lipschitz constant of generative models. We relate this quantity to the maximal norm over the set of attainable vector-Jacobian products of a given generative model. We approximate this set by layerwise convex approximations using zonotopes. Our approach generalizes and improves upon prior work using zonotope transformers and we extend to Lipschitz estimation of neural networks with large output dimension. This provides efficient and tight bounds on small networks and can scale to generative models on VAE and DCGAN architectures.

Exactly Computing the Local Lipschitz Constant of ReLU Networks

The Lipschitz constant of a neural network is a useful metric for provable robustness and generalization. We present a novel analytic result which relates gradient norms to Lipschitz constants for nondifferentiable functions. Next we prove hardness and inapproximability results for computing the local Lipschitz constant of ReLU neural networks. We develop a mixed-integer programming formulation to exactly compute the local Lipschitz constant for scalar and vector-valued networks. Finally, we apply our technique on networks trained on synthetic datasets and MNIST, drawing observations about the tightness of competing Lipschitz estimators and the effects of regularized training on Lipschitz constants.