Decomposing Epistemic Uncertainty for Causal Decision Making

Causal inference from observational data provides strong evidence for the best action in decision-making without performing expensive randomized trials. The effect of an action is usually not identifiable under unobserved confounding, even with an infinite amount of data. Recent work uses neural networks to obtain practical bounds to such causal effects, which is often an intractable problem. However, these approaches may overfit to the dataset and be overconfident in their causal effect estimates. Moreover, there is currently no systematic approach to disentangle how much of the width of causal effect bounds is due to fundamental non-identifiability versus how much is due to finite-sample limitations. We propose a novel framework to address this problem by considering a confidence set around the empirical observational distribution and obtaining the intersection of causal effect bounds for all distributions in this confidence set. This allows us to distinguish the part of the interval that can be reduced by collecting more samples, which we call sample uncertainty, from the part that can only be reduced by observing more variables, such as latent confounders or instrumental variables, but not with more data, which we call non-ID uncertainty. The upper and lower bounds to this intersection are obtained by solving min-max and max-min problems with neural causal models by searching over all distributions that the dataset might have been sampled from, and all SCMs that entail the corresponding distribution. We demonstrate via extensive experiments on synthetic and real-world datasets that our algorithm can determine when collecting more samples will not help determine the best action. This can guide practitioners to collect more variables or lean towards a randomized study for best action identification.

Conditional Generative Models are Sufficient to Sample from Any Causal Effect Estimand

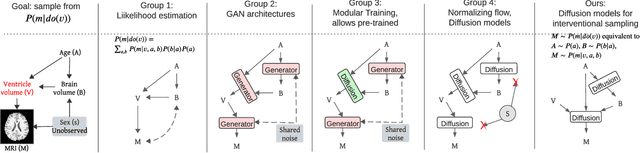
Causal inference from observational data has recently found many applications in machine learning. While sound and complete algorithms exist to compute causal effects, many of these algorithms require explicit access to conditional likelihoods over the observational distribution, which is difficult to estimate in the high-dimensional regime, such as with images. To alleviate this issue, researchers have approached the problem by simulating causal relations with neural models and obtained impressive results. However, none of these existing approaches can be applied to generic scenarios such as causal graphs on image data with latent confounders, or obtain conditional interventional samples. In this paper, we show that any identifiable causal effect given an arbitrary causal graph can be computed through push-forward computations of conditional generative models. Based on this result, we devise a diffusion-based approach to sample from any (conditional) interventional distribution on image data. To showcase our algorithm's performance, we conduct experiments on a Colored MNIST dataset having both the treatment ($X$) and the target variables ($Y$) as images and obtain interventional samples from $P(y|do(x))$. As an application of our algorithm, we evaluate two large conditional generative models that are pre-trained on the CelebA dataset by analyzing the strength of spurious correlations and the level of disentanglement they achieve.

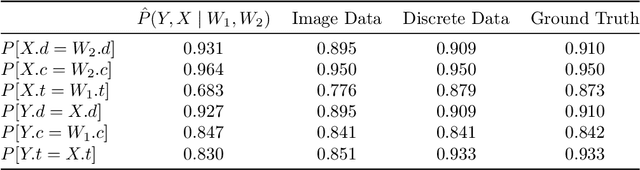
Modular Learning of Deep Causal Generative Models for High-dimensional Causal Inference

Pearl's causal hierarchy establishes a clear separation between observational, interventional, and counterfactual questions. Researchers proposed sound and complete algorithms to compute identifiable causal queries at a given level of the hierarchy using the causal structure and data from the lower levels of the hierarchy. However, most of these algorithms assume that we can accurately estimate the probability distribution of the data, which is an impractical assumption for high-dimensional variables such as images. On the other hand, modern generative deep learning architectures can be trained to learn how to accurately sample from such high-dimensional distributions. Especially with the recent rise of foundation models for images, it is desirable to leverage pre-trained models to answer causal queries with such high-dimensional data. To address this, we propose a sequential training algorithm that, given the causal structure and a pre-trained conditional generative model, can train a deep causal generative model, which utilizes the pre-trained model and can provably sample from identifiable interventional and counterfactual distributions. Our algorithm, called Modular-DCM, uses adversarial training to learn the network weights, and to the best of our knowledge, is the first algorithm that can make use of pre-trained models and provably sample from any identifiable causal query in the presence of latent confounders with high-dimensional data. We demonstrate the utility of our algorithm using semi-synthetic and real-world datasets containing images as variables in the causal structure.