Partial Structure Discovery is Sufficient for No-regret Learning in Causal Bandits

Causal knowledge about the relationships among decision variables and a reward variable in a bandit setting can accelerate the learning of an optimal decision. Current works often assume the causal graph is known, which may not always be available a priori. Motivated by this challenge, we focus on the causal bandit problem in scenarios where the underlying causal graph is unknown and may include latent confounders. While intervention on the parents of the reward node is optimal in the absence of latent confounders, this is not necessarily the case in general. Instead, one must consider a set of possibly optimal arms/interventions, each being a special subset of the ancestors of the reward node, making causal discovery beyond the parents of the reward node essential. For regret minimization, we identify that discovering the full causal structure is unnecessary; however, no existing work provides the necessary and sufficient components of the causal graph. We formally characterize the set of necessary and sufficient latent confounders one needs to detect or learn to ensure that all possibly optimal arms are identified correctly. We also propose a randomized algorithm for learning the causal graph with a limited number of samples, providing a sample complexity guarantee for any desired confidence level. In the causal bandit setup, we propose a two-stage approach. In the first stage, we learn the induced subgraph on ancestors of the reward, along with a necessary and sufficient subset of latent confounders, to construct the set of possibly optimal arms. The regret incurred during this phase scales polynomially with respect to the number of nodes in the causal graph. The second phase involves the application of a standard bandit algorithm, such as the UCB algorithm. We also establish a regret bound for our two-phase approach, which is sublinear in the number of rounds.

Sample Efficient Bayesian Learning of Causal Graphs from Interventions

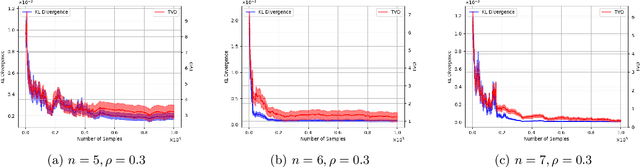
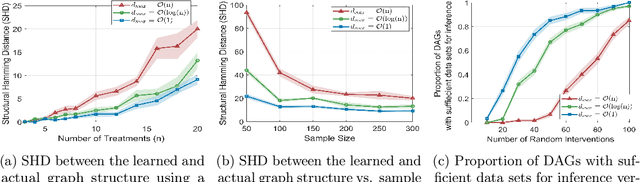
Causal discovery is a fundamental problem with applications spanning various areas in science and engineering. It is well understood that solely using observational data, one can only orient the causal graph up to its Markov equivalence class, necessitating interventional data to learn the complete causal graph. Most works in the literature design causal discovery policies with perfect interventions, i.e., they have access to infinite interventional samples. This study considers a Bayesian approach for learning causal graphs with limited interventional samples, mirroring real-world scenarios where such samples are usually costly to obtain. By leveraging the recent result of Wien\"obst et al. (2023) on uniform DAG sampling in polynomial time, we can efficiently enumerate all the cut configurations and their corresponding interventional distributions of a target set, and further track their posteriors. Given any number of interventional samples, our proposed algorithm randomly intervenes on a set of target vertices that cut all the edges in the graph and returns a causal graph according to the posterior of each target set. When the number of interventional samples is large enough, we show theoretically that our proposed algorithm will return the true causal graph with high probability. We compare our algorithm against various baseline methods on simulated datasets, demonstrating its superior accuracy measured by the structural Hamming distance between the learned DAG and the ground truth. Additionally, we present a case study showing how this algorithm could be modified to answer more general causal questions without learning the whole graph. As an example, we illustrate that our method can be used to estimate the causal effect of a variable that cannot be intervened.

Counterfactual Fairness by Combining Factual and Counterfactual Predictions

In high-stake domains such as healthcare and hiring, the role of machine learning (ML) in decision-making raises significant fairness concerns. This work focuses on Counterfactual Fairness (CF), which posits that an ML model's outcome on any individual should remain unchanged if they had belonged to a different demographic group. Previous works have proposed methods that guarantee CF. Notwithstanding, their effects on the model's predictive performance remains largely unclear. To fill in this gap, we provide a theoretical study on the inherent trade-off between CF and predictive performance in a model-agnostic manner. We first propose a simple but effective method to cast an optimal but potentially unfair predictor into a fair one without losing the optimality. By analyzing its excess risk in order to achieve CF, we quantify this inherent trade-off. Further analysis on our method's performance with access to only incomplete causal knowledge is also conducted. Built upon it, we propose a performant algorithm that can be applied in such scenarios. Experiments on both synthetic and semi-synthetic datasets demonstrate the validity of our analysis and methods.

Identification of Average Causal Effects in Confounded Additive Noise Models

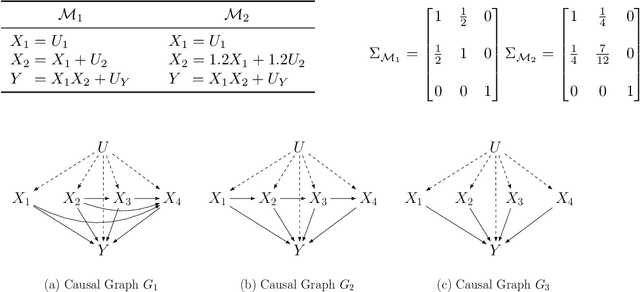
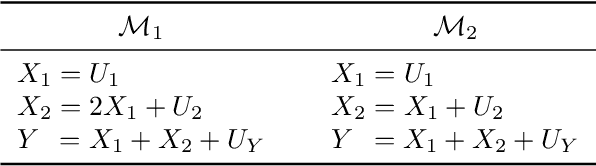
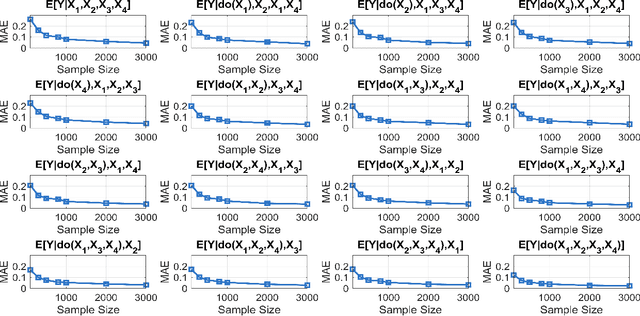
Additive noise models (ANMs) are an important setting studied in causal inference. Most of the existing works on ANMs assume causal sufficiency, i.e., there are no unobserved confounders. This paper focuses on confounded ANMs, where a set of treatment variables and a target variable are affected by an unobserved confounder that follows a multivariate Gaussian distribution. We introduce a novel approach for estimating the average causal effects (ACEs) of any subset of the treatment variables on the outcome and demonstrate that a small set of interventional distributions is sufficient to estimate all of them. In addition, we propose a randomized algorithm that further reduces the number of required interventions to poly-logarithmic in the number of nodes. Finally, we demonstrate that these interventions are also sufficient to recover the causal structure between the observed variables. This establishes that a poly-logarithmic number of interventions is sufficient to infer the causal effects of any subset of treatments on the outcome in confounded ANMs with high probability, even when the causal structure between treatments is unknown. The simulation results indicate that our method can accurately estimate all ACEs in the finite-sample regime. We also demonstrate the practical significance of our algorithm by evaluating it on semi-synthetic data.

Causal Discovery-Driven Change Point Detection in Time Series

Change point detection in time series seeks to identify times when the probability distribution of time series changes. It is widely applied in many areas, such as human-activity sensing and medical science. In the context of multivariate time series, this typically involves examining the joint distribution of high-dimensional data: If any one variable changes, the whole time series is assumed to have changed. However, in practical applications, we may be interested only in certain components of the time series, exploring abrupt changes in their distributions in the presence of other time series. Here, assuming an underlying structural causal model that governs the time-series data generation, we address this problem by proposing a two-stage non-parametric algorithm that first learns parts of the causal structure through constraint-based discovery methods. The algorithm then uses conditional relative Pearson divergence estimation to identify the change points. The conditional relative Pearson divergence quantifies the distribution disparity between consecutive segments in the time series, while the causal discovery method enables a focus on the causal mechanism, facilitating access to independent and identically distributed (IID) samples. Theoretically, the typical assumption of samples being IID in conventional change point detection methods can be relaxed based on the Causal Markov Condition. Through experiments on both synthetic and real-world datasets, we validate the correctness and utility of our approach.

Causal Discovery in Semi-Stationary Time Series

Discovering causal relations from observational time series without making the stationary assumption is a significant challenge. In practice, this challenge is common in many areas, such as retail sales, transportation systems, and medical science. Here, we consider this problem for a class of non-stationary time series. The structural causal model (SCM) of this type of time series, called the semi-stationary time series, exhibits that a finite number of different causal mechanisms occur sequentially and periodically across time. This model holds considerable practical utility because it can represent periodicity, including common occurrences such as seasonality and diurnal variation. We propose a constraint-based, non-parametric algorithm for discovering causal relations in this setting. The resulting algorithm, PCMCI$_{\Omega}$, can capture the alternating and recurring changes in the causal mechanisms and then identify the underlying causal graph with conditional independence (CI) tests. We show that this algorithm is sound in identifying causal relations on discrete time series. We validate the algorithm with extensive experiments on continuous and discrete simulated data. We also apply our algorithm to a real-world climate dataset.

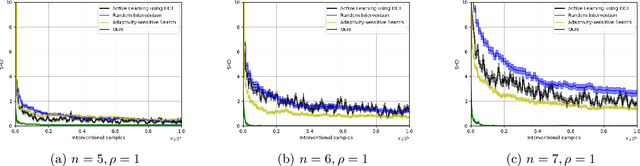
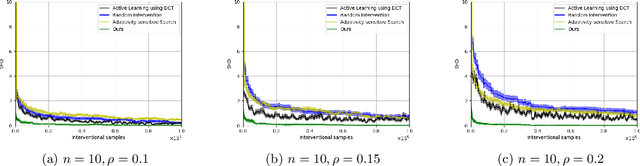
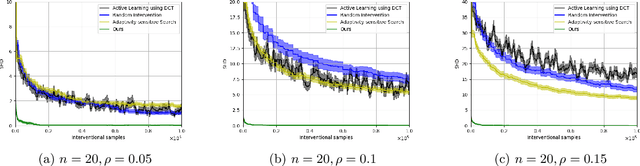
Adaptive Online Experimental Design for Causal Discovery

Causal discovery aims to uncover cause-and-effect relationships encoded in causal graphs by leveraging observational, interventional data, or their combination. The majority of existing causal discovery methods are developed assuming infinite interventional data. We focus on data interventional efficiency and formalize causal discovery from the perspective of online learning, inspired by pure exploration in bandit problems. A graph separating system, consisting of interventions that cut every edge of the graph at least once, is sufficient for learning causal graphs when infinite interventional data is available, even in the worst case. We propose a track-and-stop causal discovery algorithm that adaptively selects interventions from the graph separating system via allocation matching and learns the causal graph based on sampling history. Given any desired confidence value, the algorithm determines a termination condition and runs until it is met. We analyze the algorithm to establish a problem-dependent upper bound on the expected number of required interventional samples. Our proposed algorithm outperforms existing methods in simulations across various randomly generated causal graphs. It achieves higher accuracy, measured by the structural hamming distance (SHD) between the learned causal graph and the ground truth, with significantly fewer samples.

Conditional Generative Models are Sufficient to Sample from Any Causal Effect Estimand

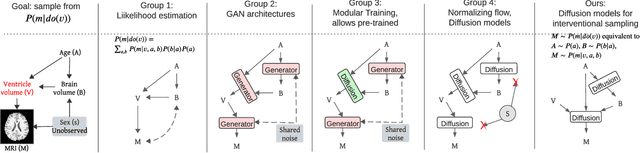
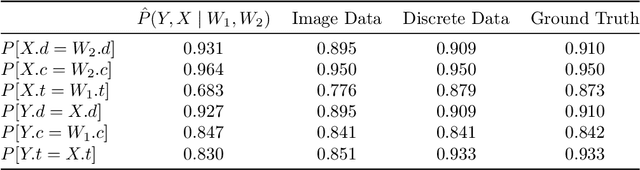
Causal inference from observational data has recently found many applications in machine learning. While sound and complete algorithms exist to compute causal effects, many of these algorithms require explicit access to conditional likelihoods over the observational distribution, which is difficult to estimate in the high-dimensional regime, such as with images. To alleviate this issue, researchers have approached the problem by simulating causal relations with neural models and obtained impressive results. However, none of these existing approaches can be applied to generic scenarios such as causal graphs on image data with latent confounders, or obtain conditional interventional samples. In this paper, we show that any identifiable causal effect given an arbitrary causal graph can be computed through push-forward computations of conditional generative models. Based on this result, we devise a diffusion-based approach to sample from any (conditional) interventional distribution on image data. To showcase our algorithm's performance, we conduct experiments on a Colored MNIST dataset having both the treatment ($X$) and the target variables ($Y$) as images and obtain interventional samples from $P(y|do(x))$. As an application of our algorithm, we evaluate two large conditional generative models that are pre-trained on the CelebA dataset by analyzing the strength of spurious correlations and the level of disentanglement they achieve.

Modular Learning of Deep Causal Generative Models for High-dimensional Causal Inference

Pearl's causal hierarchy establishes a clear separation between observational, interventional, and counterfactual questions. Researchers proposed sound and complete algorithms to compute identifiable causal queries at a given level of the hierarchy using the causal structure and data from the lower levels of the hierarchy. However, most of these algorithms assume that we can accurately estimate the probability distribution of the data, which is an impractical assumption for high-dimensional variables such as images. On the other hand, modern generative deep learning architectures can be trained to learn how to accurately sample from such high-dimensional distributions. Especially with the recent rise of foundation models for images, it is desirable to leverage pre-trained models to answer causal queries with such high-dimensional data. To address this, we propose a sequential training algorithm that, given the causal structure and a pre-trained conditional generative model, can train a deep causal generative model, which utilizes the pre-trained model and can provably sample from identifiable interventional and counterfactual distributions. Our algorithm, called Modular-DCM, uses adversarial training to learn the network weights, and to the best of our knowledge, is the first algorithm that can make use of pre-trained models and provably sample from any identifiable causal query in the presence of latent confounders with high-dimensional data. We demonstrate the utility of our algorithm using semi-synthetic and real-world datasets containing images as variables in the causal structure.

Approximate Causal Effect Identification under Weak Confounding

Causal effect estimation has been studied by many researchers when only observational data is available. Sound and complete algorithms have been developed for pointwise estimation of identifiable causal queries. For non-identifiable causal queries, researchers developed polynomial programs to estimate tight bounds on causal effect. However, these are computationally difficult to optimize for variables with large support sizes. In this paper, we analyze the effect of "weak confounding" on causal estimands. More specifically, under the assumption that the unobserved confounders that render a query non-identifiable have small entropy, we propose an efficient linear program to derive the upper and lower bounds of the causal effect. We show that our bounds are consistent in the sense that as the entropy of unobserved confounders goes to zero, the gap between the upper and lower bound vanishes. Finally, we conduct synthetic and real data simulations to compare our bounds with the bounds obtained by the existing work that cannot incorporate such entropy constraints and show that our bounds are tighter for the setting with weak confounders.