Sample Efficient Bayesian Learning of Causal Graphs from Interventions

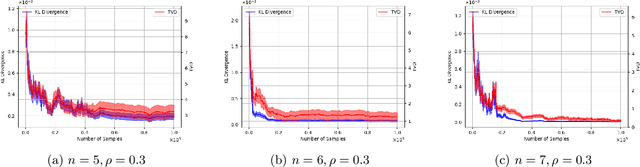
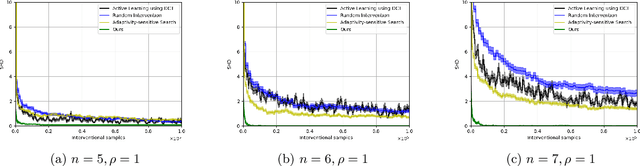
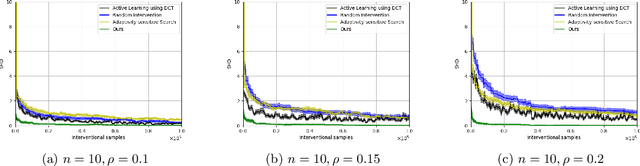
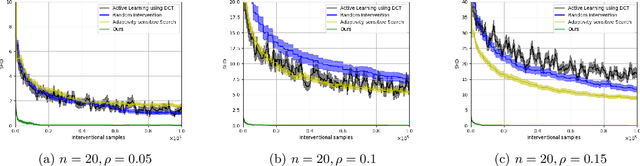
Causal discovery is a fundamental problem with applications spanning various areas in science and engineering. It is well understood that solely using observational data, one can only orient the causal graph up to its Markov equivalence class, necessitating interventional data to learn the complete causal graph. Most works in the literature design causal discovery policies with perfect interventions, i.e., they have access to infinite interventional samples. This study considers a Bayesian approach for learning causal graphs with limited interventional samples, mirroring real-world scenarios where such samples are usually costly to obtain. By leveraging the recent result of Wien\"obst et al. (2023) on uniform DAG sampling in polynomial time, we can efficiently enumerate all the cut configurations and their corresponding interventional distributions of a target set, and further track their posteriors. Given any number of interventional samples, our proposed algorithm randomly intervenes on a set of target vertices that cut all the edges in the graph and returns a causal graph according to the posterior of each target set. When the number of interventional samples is large enough, we show theoretically that our proposed algorithm will return the true causal graph with high probability. We compare our algorithm against various baseline methods on simulated datasets, demonstrating its superior accuracy measured by the structural Hamming distance between the learned DAG and the ground truth. Additionally, we present a case study showing how this algorithm could be modified to answer more general causal questions without learning the whole graph. As an example, we illustrate that our method can be used to estimate the causal effect of a variable that cannot be intervened.