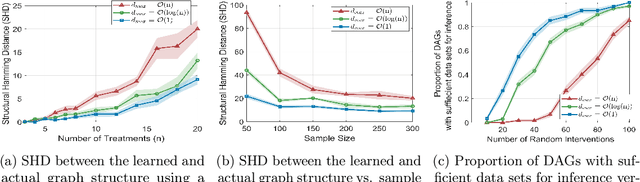
Partial Structure Discovery is Sufficient for No-regret Learning in Causal Bandits

Causal knowledge about the relationships among decision variables and a reward variable in a bandit setting can accelerate the learning of an optimal decision. Current works often assume the causal graph is known, which may not always be available a priori. Motivated by this challenge, we focus on the causal bandit problem in scenarios where the underlying causal graph is unknown and may include latent confounders. While intervention on the parents of the reward node is optimal in the absence of latent confounders, this is not necessarily the case in general. Instead, one must consider a set of possibly optimal arms/interventions, each being a special subset of the ancestors of the reward node, making causal discovery beyond the parents of the reward node essential. For regret minimization, we identify that discovering the full causal structure is unnecessary; however, no existing work provides the necessary and sufficient components of the causal graph. We formally characterize the set of necessary and sufficient latent confounders one needs to detect or learn to ensure that all possibly optimal arms are identified correctly. We also propose a randomized algorithm for learning the causal graph with a limited number of samples, providing a sample complexity guarantee for any desired confidence level. In the causal bandit setup, we propose a two-stage approach. In the first stage, we learn the induced subgraph on ancestors of the reward, along with a necessary and sufficient subset of latent confounders, to construct the set of possibly optimal arms. The regret incurred during this phase scales polynomially with respect to the number of nodes in the causal graph. The second phase involves the application of a standard bandit algorithm, such as the UCB algorithm. We also establish a regret bound for our two-phase approach, which is sublinear in the number of rounds.

Sample Efficient Bayesian Learning of Causal Graphs from Interventions

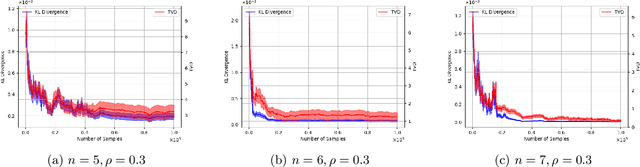
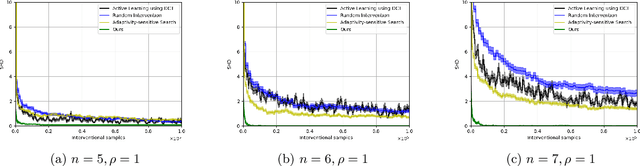
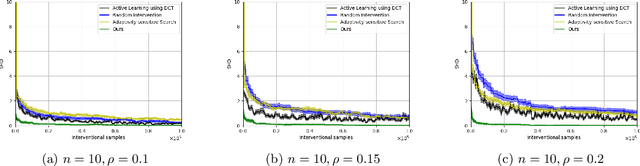
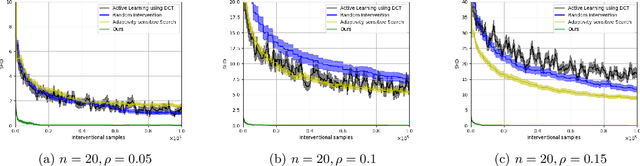
Causal discovery is a fundamental problem with applications spanning various areas in science and engineering. It is well understood that solely using observational data, one can only orient the causal graph up to its Markov equivalence class, necessitating interventional data to learn the complete causal graph. Most works in the literature design causal discovery policies with perfect interventions, i.e., they have access to infinite interventional samples. This study considers a Bayesian approach for learning causal graphs with limited interventional samples, mirroring real-world scenarios where such samples are usually costly to obtain. By leveraging the recent result of Wien\"obst et al. (2023) on uniform DAG sampling in polynomial time, we can efficiently enumerate all the cut configurations and their corresponding interventional distributions of a target set, and further track their posteriors. Given any number of interventional samples, our proposed algorithm randomly intervenes on a set of target vertices that cut all the edges in the graph and returns a causal graph according to the posterior of each target set. When the number of interventional samples is large enough, we show theoretically that our proposed algorithm will return the true causal graph with high probability. We compare our algorithm against various baseline methods on simulated datasets, demonstrating its superior accuracy measured by the structural Hamming distance between the learned DAG and the ground truth. Additionally, we present a case study showing how this algorithm could be modified to answer more general causal questions without learning the whole graph. As an example, we illustrate that our method can be used to estimate the causal effect of a variable that cannot be intervened.

Identification of Average Causal Effects in Confounded Additive Noise Models

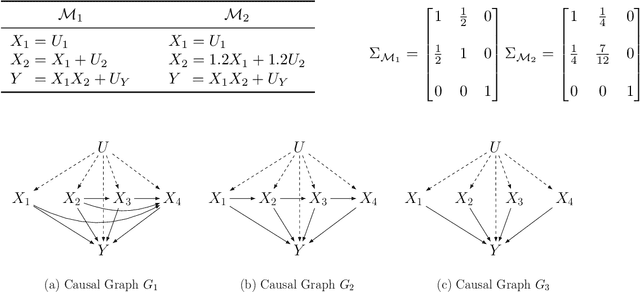
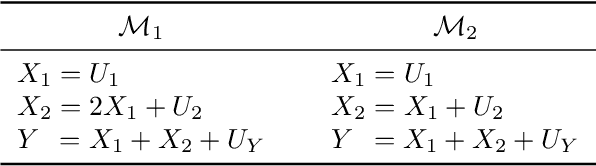
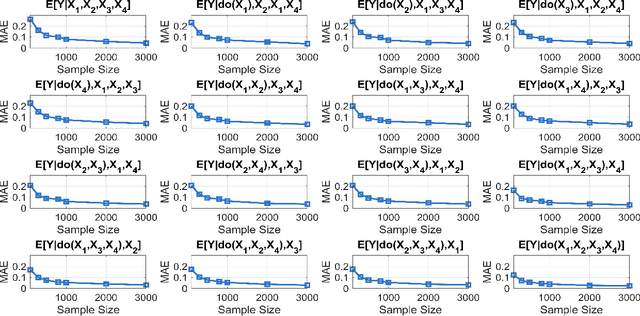
Additive noise models (ANMs) are an important setting studied in causal inference. Most of the existing works on ANMs assume causal sufficiency, i.e., there are no unobserved confounders. This paper focuses on confounded ANMs, where a set of treatment variables and a target variable are affected by an unobserved confounder that follows a multivariate Gaussian distribution. We introduce a novel approach for estimating the average causal effects (ACEs) of any subset of the treatment variables on the outcome and demonstrate that a small set of interventional distributions is sufficient to estimate all of them. In addition, we propose a randomized algorithm that further reduces the number of required interventions to poly-logarithmic in the number of nodes. Finally, we demonstrate that these interventions are also sufficient to recover the causal structure between the observed variables. This establishes that a poly-logarithmic number of interventions is sufficient to infer the causal effects of any subset of treatments on the outcome in confounded ANMs with high probability, even when the causal structure between treatments is unknown. The simulation results indicate that our method can accurately estimate all ACEs in the finite-sample regime. We also demonstrate the practical significance of our algorithm by evaluating it on semi-synthetic data.

Adaptive Online Experimental Design for Causal Discovery

Causal discovery aims to uncover cause-and-effect relationships encoded in causal graphs by leveraging observational, interventional data, or their combination. The majority of existing causal discovery methods are developed assuming infinite interventional data. We focus on data interventional efficiency and formalize causal discovery from the perspective of online learning, inspired by pure exploration in bandit problems. A graph separating system, consisting of interventions that cut every edge of the graph at least once, is sufficient for learning causal graphs when infinite interventional data is available, even in the worst case. We propose a track-and-stop causal discovery algorithm that adaptively selects interventions from the graph separating system via allocation matching and learns the causal graph based on sampling history. Given any desired confidence value, the algorithm determines a termination condition and runs until it is met. We analyze the algorithm to establish a problem-dependent upper bound on the expected number of required interventional samples. Our proposed algorithm outperforms existing methods in simulations across various randomly generated causal graphs. It achieves higher accuracy, measured by the structural hamming distance (SHD) between the learned causal graph and the ground truth, with significantly fewer samples.