Identification of Average Causal Effects in Confounded Additive Noise Models
Paper and Code
Jul 13, 2024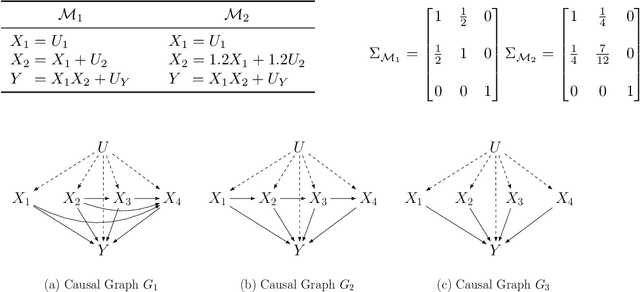
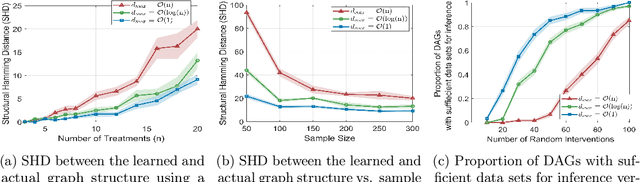
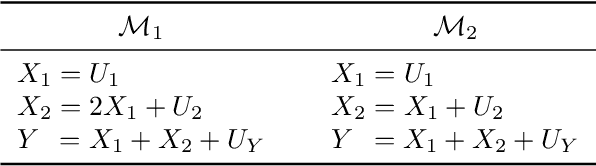
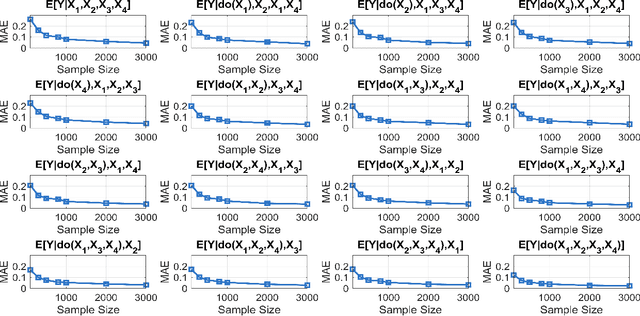
Additive noise models (ANMs) are an important setting studied in causal inference. Most of the existing works on ANMs assume causal sufficiency, i.e., there are no unobserved confounders. This paper focuses on confounded ANMs, where a set of treatment variables and a target variable are affected by an unobserved confounder that follows a multivariate Gaussian distribution. We introduce a novel approach for estimating the average causal effects (ACEs) of any subset of the treatment variables on the outcome and demonstrate that a small set of interventional distributions is sufficient to estimate all of them. In addition, we propose a randomized algorithm that further reduces the number of required interventions to poly-logarithmic in the number of nodes. Finally, we demonstrate that these interventions are also sufficient to recover the causal structure between the observed variables. This establishes that a poly-logarithmic number of interventions is sufficient to infer the causal effects of any subset of treatments on the outcome in confounded ANMs with high probability, even when the causal structure between treatments is unknown. The simulation results indicate that our method can accurately estimate all ACEs in the finite-sample regime. We also demonstrate the practical significance of our algorithm by evaluating it on semi-synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge