Mahsa Ghasemi
Reinforcement Learning from Multi-level and Episodic Human Feedback
Apr 20, 2025


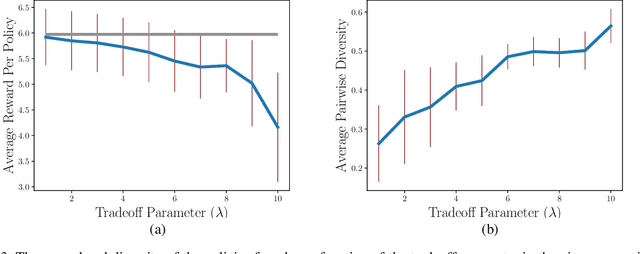
Abstract:Designing an effective reward function has long been a challenge in reinforcement learning, particularly for complex tasks in unstructured environments. To address this, various learning paradigms have emerged that leverage different forms of human input to specify or refine the reward function. Reinforcement learning from human feedback is a prominent approach that utilizes human comparative feedback, expressed as a preference for one behavior over another, to tackle this problem. In contrast to comparative feedback, we explore multi-level human feedback, which is provided in the form of a score at the end of each episode. This type of feedback offers more coarse but informative signals about the underlying reward function than binary feedback. Additionally, it can handle non-Markovian rewards, as it is based on the evaluation of an entire episode. We propose an algorithm to efficiently learn both the reward function and the optimal policy from this form of feedback. Moreover, we show that the proposed algorithm achieves sublinear regret and demonstrate its empirical effectiveness through extensive simulations.
Robust Information Selection for Hypothesis Testing with Misclassification Penalties
Feb 21, 2025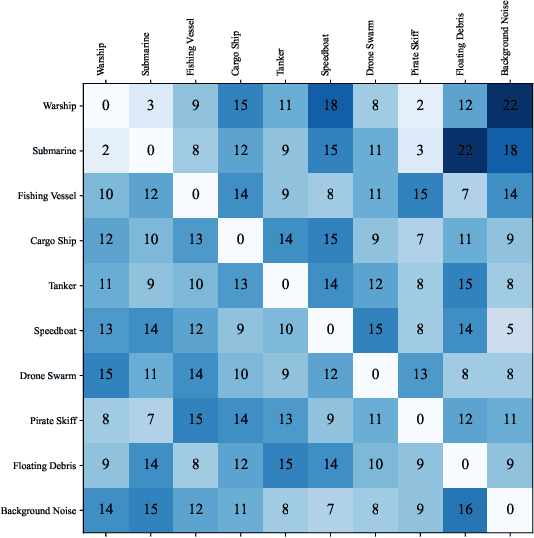
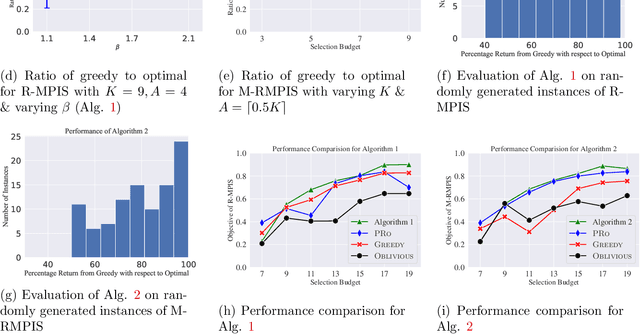
Abstract:We study the problem of robust information selection for a Bayesian hypothesis testing / classification task, where the goal is to identify the true state of the world from a finite set of hypotheses based on observations from the selected information sources. We introduce a novel misclassification penalty framework, which enables non-uniform treatment of different misclassification events. Extending the classical subset selection framework, we study the problem of selecting a subset of sources that minimize the maximum penalty of misclassification under a limited budget, despite deletions or failures of a subset of the selected sources. We characterize the curvature properties of the objective function and propose an efficient greedy algorithm with performance guarantees. Next, we highlight certain limitations of optimizing for the maximum penalty metric and propose a submodular surrogate metric to guide the selection of the information set. We propose a greedy algorithm with near-optimality guarantees for optimizing the surrogate metric. Finally, we empirically demonstrate the performance of our proposed algorithms in several instances of the information set selection problem.
Partial Structure Discovery is Sufficient for No-regret Learning in Causal Bandits
Nov 06, 2024



Abstract:Causal knowledge about the relationships among decision variables and a reward variable in a bandit setting can accelerate the learning of an optimal decision. Current works often assume the causal graph is known, which may not always be available a priori. Motivated by this challenge, we focus on the causal bandit problem in scenarios where the underlying causal graph is unknown and may include latent confounders. While intervention on the parents of the reward node is optimal in the absence of latent confounders, this is not necessarily the case in general. Instead, one must consider a set of possibly optimal arms/interventions, each being a special subset of the ancestors of the reward node, making causal discovery beyond the parents of the reward node essential. For regret minimization, we identify that discovering the full causal structure is unnecessary; however, no existing work provides the necessary and sufficient components of the causal graph. We formally characterize the set of necessary and sufficient latent confounders one needs to detect or learn to ensure that all possibly optimal arms are identified correctly. We also propose a randomized algorithm for learning the causal graph with a limited number of samples, providing a sample complexity guarantee for any desired confidence level. In the causal bandit setup, we propose a two-stage approach. In the first stage, we learn the induced subgraph on ancestors of the reward, along with a necessary and sufficient subset of latent confounders, to construct the set of possibly optimal arms. The regret incurred during this phase scales polynomially with respect to the number of nodes in the causal graph. The second phase involves the application of a standard bandit algorithm, such as the UCB algorithm. We also establish a regret bound for our two-phase approach, which is sublinear in the number of rounds.
Identification of Average Causal Effects in Confounded Additive Noise Models
Jul 13, 2024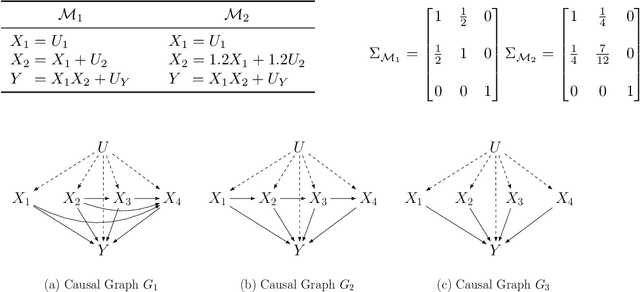
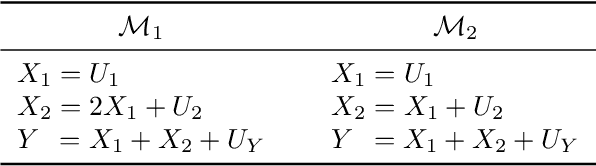
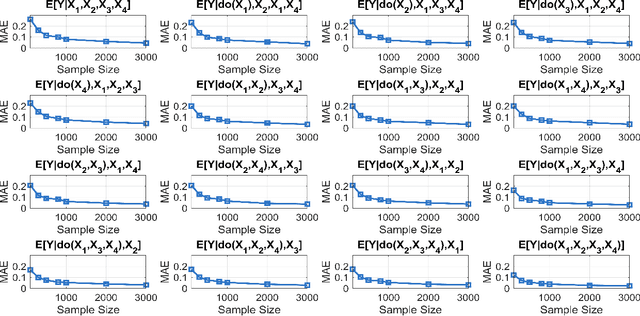
Abstract:Additive noise models (ANMs) are an important setting studied in causal inference. Most of the existing works on ANMs assume causal sufficiency, i.e., there are no unobserved confounders. This paper focuses on confounded ANMs, where a set of treatment variables and a target variable are affected by an unobserved confounder that follows a multivariate Gaussian distribution. We introduce a novel approach for estimating the average causal effects (ACEs) of any subset of the treatment variables on the outcome and demonstrate that a small set of interventional distributions is sufficient to estimate all of them. In addition, we propose a randomized algorithm that further reduces the number of required interventions to poly-logarithmic in the number of nodes. Finally, we demonstrate that these interventions are also sufficient to recover the causal structure between the observed variables. This establishes that a poly-logarithmic number of interventions is sufficient to infer the causal effects of any subset of treatments on the outcome in confounded ANMs with high probability, even when the causal structure between treatments is unknown. The simulation results indicate that our method can accurately estimate all ACEs in the finite-sample regime. We also demonstrate the practical significance of our algorithm by evaluating it on semi-synthetic data.
Adaptive Online Experimental Design for Causal Discovery
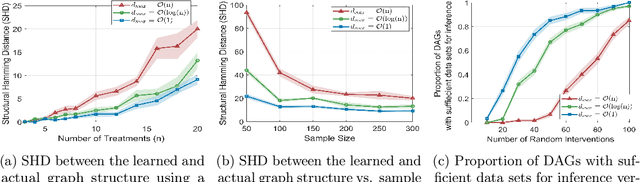
May 19, 2024Abstract:Causal discovery aims to uncover cause-and-effect relationships encoded in causal graphs by leveraging observational, interventional data, or their combination. The majority of existing causal discovery methods are developed assuming infinite interventional data. We focus on data interventional efficiency and formalize causal discovery from the perspective of online learning, inspired by pure exploration in bandit problems. A graph separating system, consisting of interventions that cut every edge of the graph at least once, is sufficient for learning causal graphs when infinite interventional data is available, even in the worst case. We propose a track-and-stop causal discovery algorithm that adaptively selects interventions from the graph separating system via allocation matching and learns the causal graph based on sampling history. Given any desired confidence value, the algorithm determines a termination condition and runs until it is met. We analyze the algorithm to establish a problem-dependent upper bound on the expected number of required interventional samples. Our proposed algorithm outperforms existing methods in simulations across various randomly generated causal graphs. It achieves higher accuracy, measured by the structural hamming distance (SHD) between the learned causal graph and the ground truth, with significantly fewer samples.
Submodular Information Selection for Hypothesis Testing with Misclassification Penalties
May 17, 2024Abstract:We consider the problem of selecting an optimal subset of information sources for a hypothesis testing/classification task where the goal is to identify the true state of the world from a finite set of hypotheses, based on finite observation samples from the sources. In order to characterize the learning performance, we propose a misclassification penalty framework, which enables non-uniform treatment of different misclassification errors. In a centralized Bayesian learning setting, we study two variants of the subset selection problem: (i) selecting a minimum cost information set to ensure that the maximum penalty of misclassifying the true hypothesis remains bounded and (ii) selecting an optimal information set under a limited budget to minimize the maximum penalty of misclassifying the true hypothesis. Under mild assumptions, we prove that the objective (or constraints) of these combinatorial optimization problems are weak (or approximate) submodular, and establish high-probability performance guarantees for greedy algorithms. Further, we propose an alternate metric for information set selection which is based on the total penalty of misclassification. We prove that this metric is submodular and establish near-optimal guarantees for the greedy algorithms for both the information set selection problems. Finally, we present numerical simulations to validate our theoretical results over several randomly generated instances.
Formal Methods for Autonomous Systems
Nov 02, 2023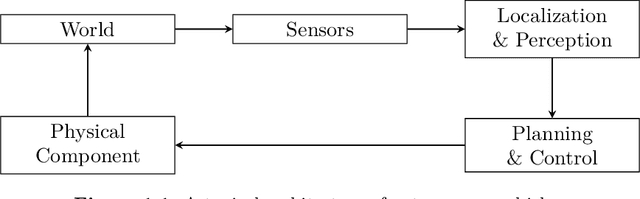
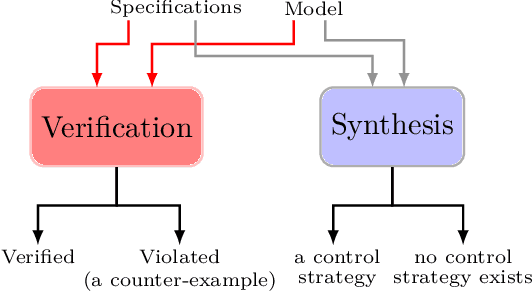
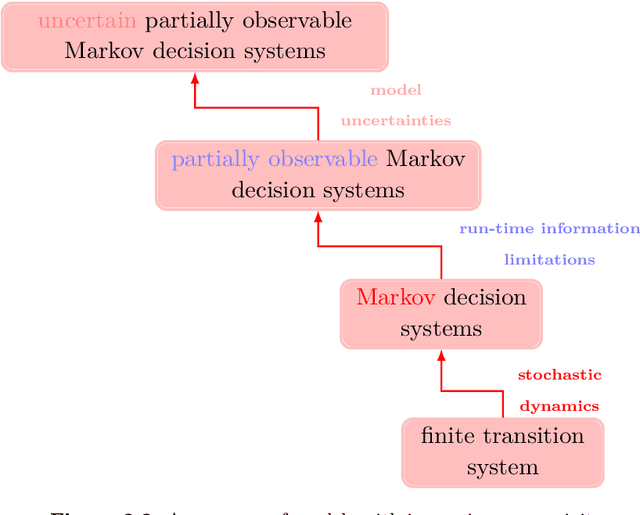
Abstract:Formal methods refer to rigorous, mathematical approaches to system development and have played a key role in establishing the correctness of safety-critical systems. The main building blocks of formal methods are models and specifications, which are analogous to behaviors and requirements in system design and give us the means to verify and synthesize system behaviors with formal guarantees. This monograph provides a survey of the current state of the art on applications of formal methods in the autonomous systems domain. We consider correct-by-construction synthesis under various formulations, including closed systems, reactive, and probabilistic settings. Beyond synthesizing systems in known environments, we address the concept of uncertainty and bound the behavior of systems that employ learning using formal methods. Further, we examine the synthesis of systems with monitoring, a mitigation technique for ensuring that once a system deviates from expected behavior, it knows a way of returning to normalcy. We also show how to overcome some limitations of formal methods themselves with learning. We conclude with future directions for formal methods in reinforcement learning, uncertainty, privacy, explainability of formal methods, and regulation and certification.
No-Regret Learning in Dynamic Stackelberg Games
Feb 10, 2022



Abstract:In a Stackelberg game, a leader commits to a randomized strategy, and a follower chooses their best strategy in response. We consider an extension of a standard Stackelberg game, called a discrete-time dynamic Stackelberg game, that has an underlying state space that affects the leader's rewards and available strategies and evolves in a Markovian manner depending on both the leader and follower's selected strategies. Although standard Stackelberg games have been utilized to improve scheduling in security domains, their deployment is often limited by requiring complete information of the follower's utility function. In contrast, we consider scenarios where the follower's utility function is unknown to the leader; however, it can be linearly parameterized. Our objective then is to provide an algorithm that prescribes a randomized strategy to the leader at each step of the game based on observations of how the follower responded in previous steps. We design a no-regret learning algorithm that, with high probability, achieves a regret bound (when compared to the best policy in hindsight) which is sublinear in the number of time steps; the degree of sublinearity depends on the number of features representing the follower's utility function. The regret of the proposed learning algorithm is independent of the size of the state space and polynomial in the rest of the parameters of the game. We show that the proposed learning algorithm outperforms existing model-free reinforcement learning approaches.
A Barrier Pair Method for Safe Human-Robot Shared Autonomy
Dec 01, 2021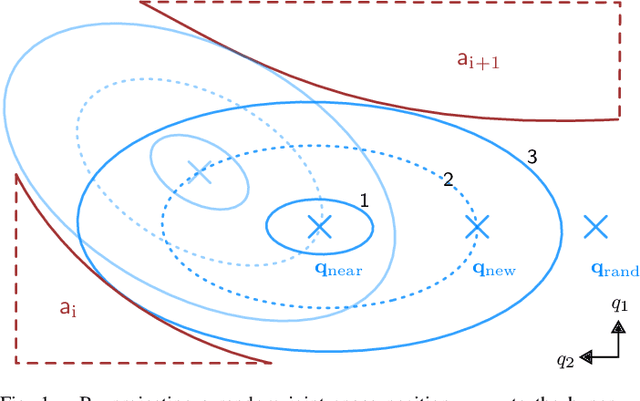
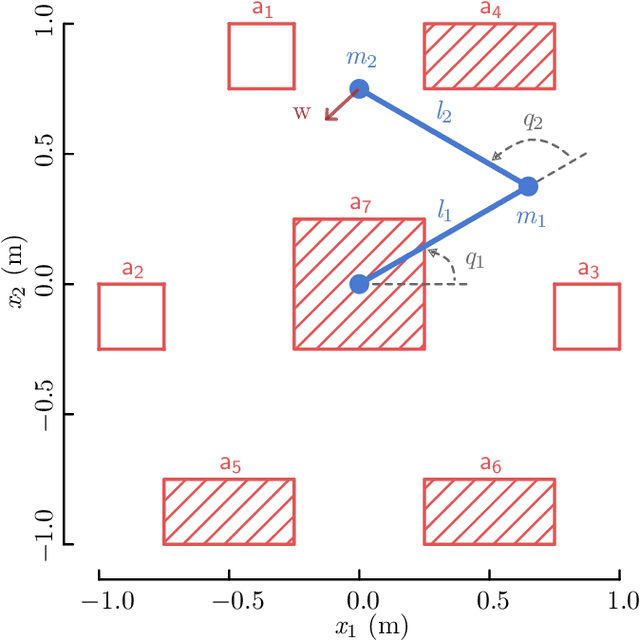
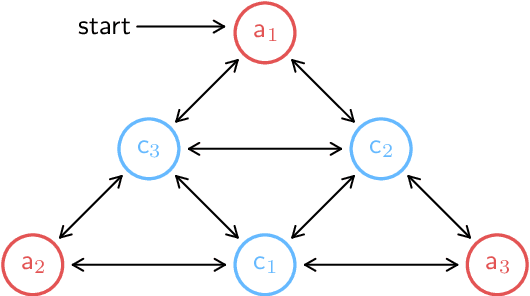
Abstract:Shared autonomy provides a framework where a human and an automated system, such as a robot, jointly control the system's behavior, enabling an effective solution for various applications, including human-robot interaction. However, a challenging problem in shared autonomy is safety because the human input may be unknown and unpredictable, which affects the robot's safety constraints. If the human input is a force applied through physical contact with the robot, it also alters the robot's behavior to maintain safety. We address the safety issue of shared autonomy in real-time applications by proposing a two-layer control framework. In the first layer, we use the history of human input measurements to infer what the human wants the robot to do and define the robot's safety constraints according to that inference. In the second layer, we formulate a rapidly-exploring random tree of barrier pairs, with each barrier pair composed of a barrier function and a controller. Using the controllers in these barrier pairs, the robot is able to maintain its safe operation under the intervention from the human input. This proposed control framework allows the robot to assist the human while preventing them from encountering safety issues. We demonstrate the proposed control framework on a simulation of a two-linkage manipulator robot.
Multiple Plans are Better than One: Diverse Stochastic Planning
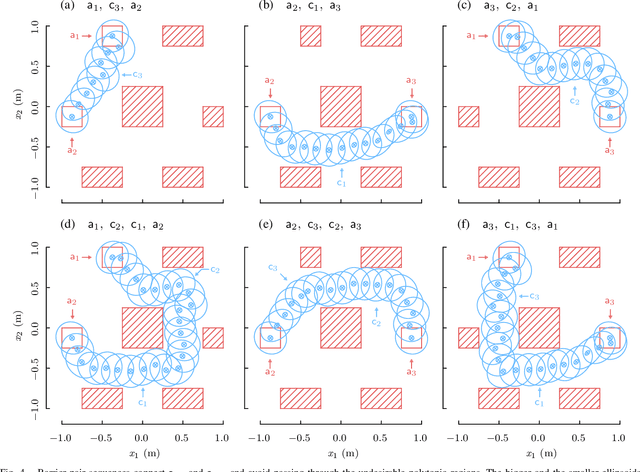
Dec 31, 2020

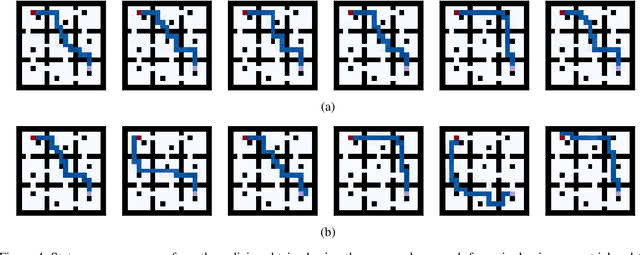
Abstract:In planning problems, it is often challenging to fully model the desired specifications. In particular, in human-robot interaction, such difficulty may arise due to human's preferences that are either private or complex to model. Consequently, the resulting objective function can only partially capture the specifications and optimizing that may lead to poor performance with respect to the true specifications. Motivated by this challenge, we formulate a problem, called diverse stochastic planning, that aims to generate a set of representative -- small and diverse -- behaviors that are near-optimal with respect to the known objective. In particular, the problem aims to compute a set of diverse and near-optimal policies for systems modeled by a Markov decision process. We cast the problem as a constrained nonlinear optimization for which we propose a solution relying on the Frank-Wolfe method. We then prove that the proposed solution converges to a stationary point and demonstrate its efficacy in several planning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge